- Submissions

Full Text
Open Access Biostatistics & Bioinformatics
Reduced Step Point Collocation Interpolation Method for the Solution of Heat Equation
Sunday Babuba*
Department of Mathematics, Federal University Dutse, Nigeria
*Corresponding author:Sunday Babuba, Department of Mathematics, Federal University Dutse, Jigawa, Nigeria.
Submission: April 4, 2018;Published: July 09, 2018

ISSN: 2577-1949 Volume2 Issue1
Abstract
In this study, we developed a new finite difference approximate method for solving heat equations. We study the numerical accuracy of the method. Detailed numerical results have shown that the method provides better results than the known explicit finite difference method. There is no semidiscretization involved and no reduction of PDE to a system of ODEs in the new approach, but rather a system of algebraic equations directly results.
Keywords: Lines; Multistep collocation; Parabolic; Taylor’s polynomial
Introduction
In this study, we will deal with a single parabolic partial differential
equation in one space variable, where and are the time and
space coordinates respectively, and the quantities and are the mesh
sizes in the space and time directions. we consider,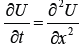 ,
0 ≤ x ≤ b, 0 ≤ t ≤ T ………. (1)
,
0 ≤ x ≤ b, 0 ≤ t ≤ T ………. (1)
Subject to the initial and boundary conditions
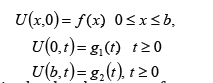
We are interested in the development of numerical techniques for solving heat equations. Of recent, there is a growing interest concerning continuous numerical methods of solution for ODEs [1- 3]. We are interested in the extension of a continuous method to solve the heat equation. This is done based on the collocation and interpolation of the PDE directly over multi steps along lines but without reduction to a system of ODEs. We intend to avoid the cost of solving a large system of coupled ODEs often arising from the reduction method by semi-discretization. The method also, eliminates the usual draw-back of stiffness arising in the conventional reduction method by semi-discretization [4,5].
The Solution Method
We subdivide the interval 0 ≤ x ≤ b into N equal subintervals by the grid points xm = mh, m =0,..., N where Nh = b .On these meshes we seek l − step approximate solution to U(x,t) of the form
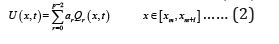
such that 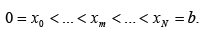 The basis function
Qr(x,t),r= 0,..., p − 2 are assumed known, ar are constants to
be determinedand p ≤ l + s , where s is the number of collocation
points. The equality holds if the number of interpolation points
used is equal to l . There will be flexibility in the choice of the basis
function Qr(x t), as may be desired for specific application. For
this work, we consider the Taylor’s polynomial
The basis function
Qr(x,t),r= 0,..., p − 2 are assumed known, ar are constants to
be determinedand p ≤ l + s , where s is the number of collocation
points. The equality holds if the number of interpolation points
used is equal to l . There will be flexibility in the choice of the basis
function Qr(x t), as may be desired for specific application. For
this work, we consider the Taylor’s polynomial 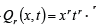 . The interpolation
values
. The interpolation
values 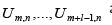 are assumed to have been determined
from previous steps, while the method seeks to obtain
are assumed to have been determined
from previous steps, while the method seeks to obtain
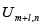 ,
[1,2,6,7]. We apply the above interpolation conditions on eqn. (2)
to obtain
,
[1,2,6,7]. We apply the above interpolation conditions on eqn. (2)
to obtain
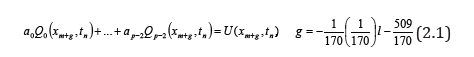
We can write eqn. (2.1) as a simple matrix equation in the augmented form as,
Using three interpolation points and one collocation point, implies that s =1, p = 4, l = 3 and r = 0,1,2.
Substituting for p in eqn. (2.1) we have,
Putting the values of g in eqn. (2.3) and writing it as matrix in
augmented form
we have,
From eqn. (2.4) we obtain the following values
Putting the above values in eqn. (2.4) becomes
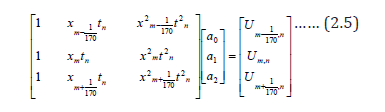
When we solve eqn. (2.5) to obtain the value of a2 to be
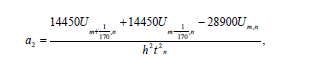
We substitute r = 0,1,2 in eqn. (2.0) to obtain
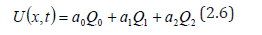
By substitution of Q0 Q1 and Q2 in eqn. (2.6) we obtain
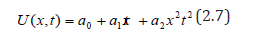
Substituting the value of a2 in eqn. (2.7) we obtain
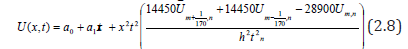
Taken the first and second derivatives of eqn. (2.8) with respect to we have
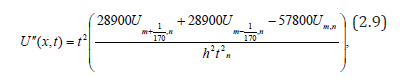
we collocate eqn. (2.9) at t = tn to arrive at
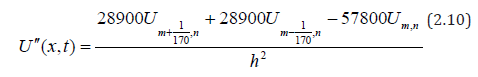
Similarly, we reverse the roles of x and t in eqn. (2.0), and we
also subdivide the interval 0 ≤ t ≤ T into y equal subintervals by the
grid points 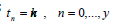 where yk = T. On these meshes we seek
l − step approximate solution to U(x,t) of the form
where yk = T. On these meshes we seek
l − step approximate solution to U(x,t) of the form
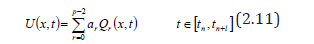
Such that 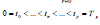 , the basis function
, the basis function 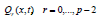 are assumed known, ar are constants to be determined and p ≤ l + s
, where s is the number of collocation points. The equality holds
if the number of interpolation points used is equal to l . There
will be flexibility in the choice of the basis function Qr(x t), as may
be desired for specific application. For this method, we consider
the Taylor’s polynomial
are assumed known, ar are constants to be determined and p ≤ l + s
, where s is the number of collocation points. The equality holds
if the number of interpolation points used is equal to l . There
will be flexibility in the choice of the basis function Qr(x t), as may
be desired for specific application. For this method, we consider
the Taylor’s polynomial 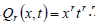 .The interpolation values
.The interpolation values
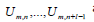 are assumed to have been determined from previous
steps, while the method seeks to obtain
are assumed to have been determined from previous
steps, while the method seeks to obtain 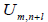 [see (4)]. We
apply the above interpolation conditions on eqn. (2.11) to obtain
[see (4)]. We
apply the above interpolation conditions on eqn. (2.11) to obtain
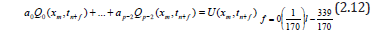
We can write (2.12) as a simple matrix equation in the augmented form

Using two interpolation points and one collocation point in eqn.
(2.13) implies that p = 3, r = 0,1 l = 2 and 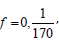 , and by substitution eqn.
(2.13) becomes
, and by substitution eqn.
(2.13) becomes
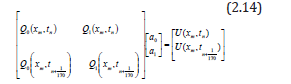
From eqn. (2.14) we obtain the following values:
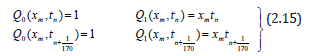
Substituting the values of eqn. (2.15) into eqn. (2.14), we have this matrix below
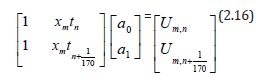
Solving eqn. (2.16) for value of a1 we obtain
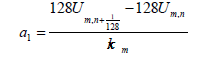
When we substitute r = 0,1, into eqn. (2.11), we obtain
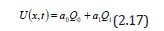
By substituting the values of 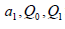 in equation (2.17) we
have
in equation (2.17) we
have
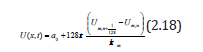
Taken the first derivatives of equation (2.18) with respect to t we obtain
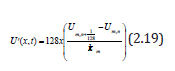
We collocate eqn. (2.19) at x = xm yields
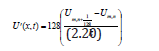
But from eqn. (1.0) we find that eqn. (2.20) is equal to eqn. (2.10), which implies that
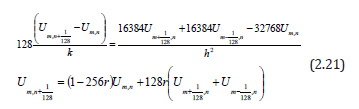
manipulating mathematically and putting 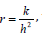 , we obtain
Eqn. (2.21) is a new scheme for solving the heat equation.
To illustrate this method, we use it to solve problems (3.1) and (3.2) respectively.
, we obtain
Eqn. (2.21) is a new scheme for solving the heat equation.
To illustrate this method, we use it to solve problems (3.1) and (3.2) respectively.
1.1. Advantages of the method
A. We intend to avoid the cost of solving a large system of
coupled ODEs often arising from the reduction methods.
B. We also intend to eliminate the usual draw-back of stiffness
arising in the conventional reduction method by semi-discretization.
Specific Problem
Example
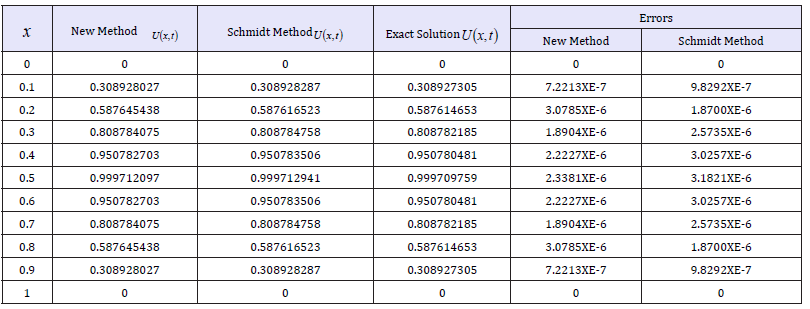
Use the scheme to approximate the solution to the heat equation (Table 1)
Table 1:Result of action of Eqn. (2.21) on problem 3.1.
Example
Table 2:Result of action of Eqn. (2.21) on problem 3.2.
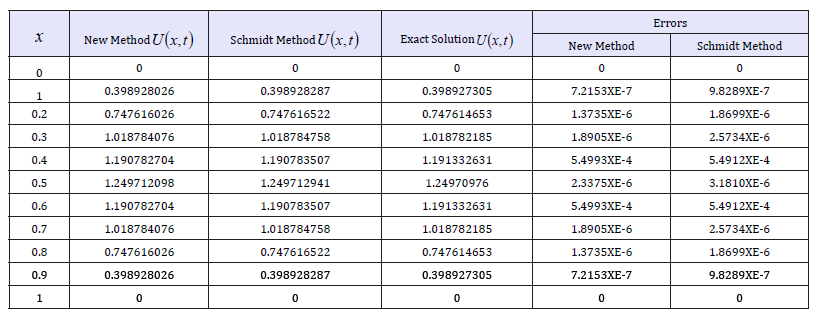
Use the scheme to approximate the solution to the heat equation (Table 2)
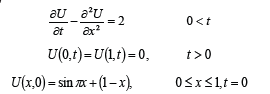
Conclusion
A continuous inter-polant is proposed for solving parabolic partial differential equation in one space variable without discretization. To check the numerical method, it is applied to solve two different test problems with known exact solutions. The numerical results confirm the validity of the new numerical scheme and suggested that it is an interesting and viable numerical method which does not involve the reduction of PDE to a system of PDE to a system of ODEs.
References
- Odekunle MR (2008) Solution of partial differential equation using collocation interpolation method.
- Pierre J (2008) Numerical solution of the dirichlet problem for elliptic parabolic equations. SIAM J Soc Indust Appl Math 6(3): 458-466.
- Ang WT (2006) Numerical solution of a non-classical parabolic problem: an integro-differential approach. Appl Math Comput 175(2): 969-979.
- Bensoussan A, Da Prato, Delfour GM, Mitter S (2007) Representation and control of infinite dimensional systems (2nd Edn), Systems & Control: Foundations & Applications, Springer, Berlin, Germany.
- Jain MK (1991) Numerical solution of differential equation. Wiley Eastern limited, New Delhi, India.
- Odekunle MR (2006) Solutions of linear evolutionary equations using lanczos-chebyshev reduction. Global Journal of Mathematics Science 5(2).
- Odekunle MR (2008) Solution of partial differential equation using collocation interpolation method. A conjecture. Paper presented at the annual conference of the Nigeria Mathematical Society, University of Lagos, Lagos, Nigeria.
© 2018 Sunday Babuba. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






