Robust Estimation in Gompertz Diffusion Model of Tumor Growth

The Gompertz diffusion process has been used in tumor growth modeling, Ferrante et al. [1]. Lo [2] considered a Gompertz diffusion model in which the size of the tumor cells is bounded and used Lie-algebraic method to derive the exact analytical solution of the functional Fokker-Planck equation obeyed by the density function of the size of the tumor. Giorno et al. [3] proposed a nonhomogeneous time dependent Gompertz diffusion process with jumps to describe the evolution of a solid tumor subject to an intermittent therapeutic program. Moummou et al. [4] obtained explicit expressions for the maximum likelihood estimators with discrete sampling from the Gompertz diffusion model by using functional optimization orthogonal projections. However, the statistical properties of the model were not studied.

Ferrante et al. [1] studied maximum likelihood estimation of natural growth parameters of tumor for such models. However, they did not study distributional properties of the estimators. The knowledge of the distribution of the estimator may be applied to evaluate the distribution of other important growing parameters used to access tumor treatment modalities. We study distributional properties of approximate minimum contrast estimators of the unknown parameters in the model from discrete data with precise rates of convergence which are robust and efficient.

Let ,P be a stochastic basis on which is defined the Gompertz diffusion process 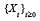satisfying the Itȏ stochastic dierential equation

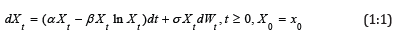
Where 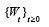is a standard Brownian motion with the filtration 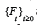and α>0; β>0; σ>0 are the unknown parameters to be estimated on the basis of discrete observations of the process {X_t} at times 0=t₀< t₁ < ....t_n=T with t_i-t_i-1= T n , i = 1,2....,n. We assume equi-spaced sampling for simplicity. We assume two types of high frequency data: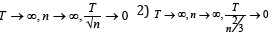

Here X_t is the tumor volume which is measured at discrete time, α is the intrinsic growth rate of the tumor, β is the tumor growth acceleration factor, and σ is the diffusion coefficient. Other parameters are the plateau of the model 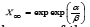tumor growth decay, and the first time the growth curve of the model reaches X∞ . We assume that the growth deceleration factor β does not change, while the variability of environmental conditions induces fluctuations in the intrinsic growth rate (mitosis rate) α. In finance literature, this model is known as Black-Karasinski model which is a geometric mean reverting Vasicek model used for modeling term structure of interest rates which preserves positivity of the interest rates.

Let the continuous realization be {X_t,0≤t≤T} denoted by . Denote Ѳ:=(α,β,σ). Let be the measure generated on the space (C_T,B_T) of continuous functions on [0,T] with the associated Borel σ algebra BT generated under the supremum norm by the process 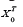and let 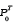be the standard Wiener measure. It is well known that when Ѳ is the true value of the parameter 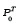is absolutely continuous with respect to 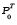and the Radon-Nikodym derivative (likelihood) of 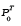with respect to 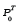based on the data 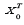is given by

Consider the log-likelihood function, which is given by

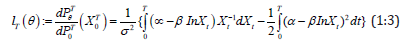
A solution of the estimating equation 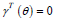provides the conditional maximum likelihood estimators (MLEs)

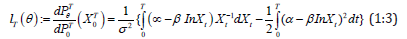
As an alternative to maximum likelihood method and to obtain robust estimators with higher efficiency we use contrast functions. Suppose α and σ are known, for simplicity let , σ=1, 1; x0=1 and our aim is to estimate the tumor growth acceleration parameter β. Using Itȏ formula, the score function can be written as

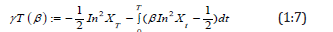
Using a contrast function which is related to the negative derivative of the log-likelihood function, we consider the estimating function,

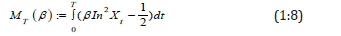
Then the minimum contrast estimate (MCE) of β which is the solution of is given by

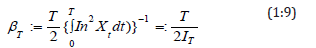
Wher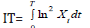e Hence 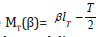. Sometimes we will denote this by just MT. We find several discrete approximations of the MCE. Define a weighted approximation of I_T:

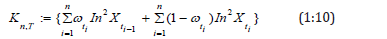
Where w_ti≥0 is a weight function. Denote the forward and backward approximations of I_T:

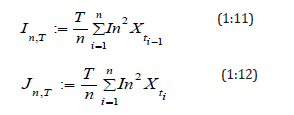
General weighted AMCE is defined as

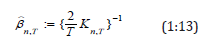
With w_ti =1 in (1.10), we obtain the forward AMCE as

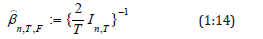
With = 0 in (1.10), we obtain the backward AMCE as

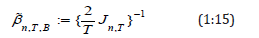
With w_(t_i )=0.5 in (1.10), the simple symmetric AMCE is defined as

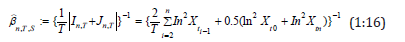
Define the weighted symmetric estimators: With the weight function

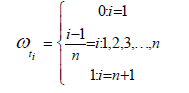
the weighted symmetric AMCE is defined as 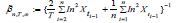Note that estimator (1.16) is analogous to the trapezoidal rule in numerical analysis. One can instead use the midpoint rule to define another estimator . One can further use the Simpson’s rule to define another estimator where the denominator is a convex combination of the trapezoidal and midpoint estimators,

The AMCE has several good properties. The AMCE is simpler to calculate, in the sense that it does not involve simulation of a stochastic integral unlike AMLE. Hence AMCE is a more practical estimator. This is robust since M-estimator is reduced to the AMCE. The AMCE is efficient, Tanaka [5]. Tanaka [5] calculated the asymptotic relative efficiency of the minimum contrast estimator with respect to least squares estimator (LSE) and showed that MCE is asymptotically efficient while LSE is inefficient. We study the distributional properties of the AMCE. We obtain the rate of weak convergence to normal distribution of the AMCE using different normings. We also obtain stochastic bound on the difference of the AMCE and its continuous counterpart MCE when T is fixed. We need the following lemmas from Bishwal [6] to prove our main results.

Lemma 1.1 Let X, Y and Z be any three random variables on a probability space (Ω,F,P) with P(Z>0)=1. Then, for any Є>0, we have

Lemma 1.2 Let Q_n, R_n, Q and R be random variables on the same probability space (Ω,F,P) with P(R_n>0)=1 and P(R_n>0)=1. Suppose where

Let Ø(.) denote the standard normal distribution function. Throughout the paper C denotes a generic constant (perhaps depending on β, but not on anything else). Since ln Xt is an Ornstein- Uhlenbeck process, we can use the following lemmas from Bishwal [6] in the sequel.

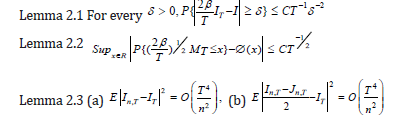
The following theorem gives the bound on the error of approximation of the distributions of the AMCE to normal distribution. Note that part (a) uses parameter dependent nonrandom norming. While this is useful for testing hypotheses about β, it may not necessarily give a confidence interval. The normings in parts (b) and (c) are sample dependent which can be used for obtaining a confidence interval. Following theorem shows that asymptotic normality of the AMCE needs the design condition

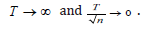
Theorem 2.1

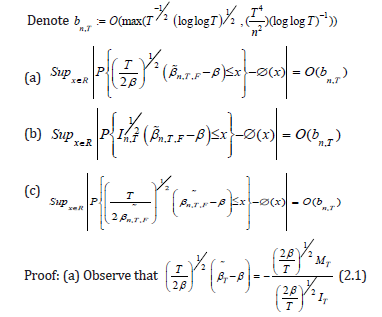
Thus, we have I Hence

(the bound for the 3^rd term in the right hand side of (2.4) is obtained from (2.3))

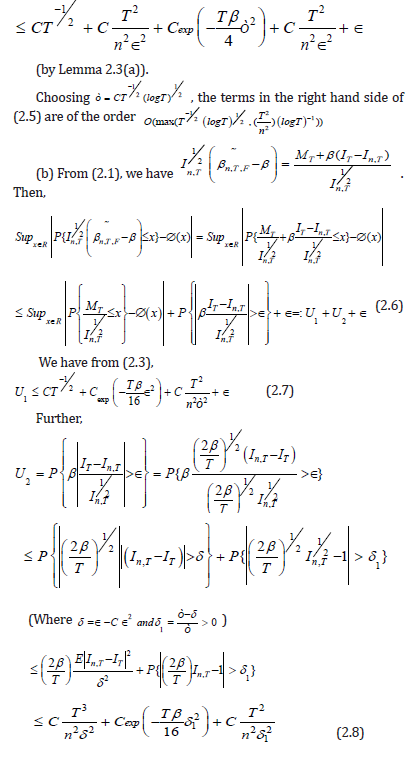
Here, the bound for the first term in the right hand side of (2.7) comes from Lemma 2.2(c) and that for the second term is obtained from (2.3) [2]. Now, using the bounds (2.7) and (2.8) in (2.6) with 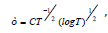, we obtain that the terms in (2.6) are of the order

On the set 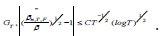. Hence, upon choosing 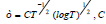large, using Lemma 1.1(b)) and Theorem 2.1(a)), we obtain

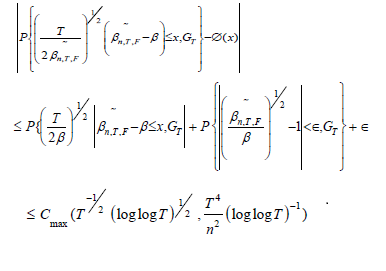
In the following theorem, we improve the bound on the error of normal approximation using a mixture of random and non-random normings. Thus asymptotic normality of the AMCEs need T → ∞ and 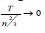which are sharper than the bound in Theorem 2.1.

Theorem 2.2

The following theorem gives stochastic bound on the error of approximation of the continuous MCE by AMCEs.

Theorem 2.3

1. Ferrante L, Bompadre S, Possati L, Leone L (2000) Parameter estimation in a Gompertzian stochastic model of tumor growth. Biometrics 56(4): 1076-1081.
2. Lo CF (2010) A modified stochastic Gompertz model for tumor cell growth. Computational and Mathematical Methods in Medicine 11(1): 3-11.
3. Giorno V, Roman P, Spina S, Torres RF (2017) Estimating a non-homogeneous Gompertz process with jumps as a model in tumor dynamics. Computational Statistics and Data Analysis 107: 18-31.
4. Moummou EK, Gutierrez R, Gutierrez SR (2012) A stochastic Gompertz model with logarithmic therapy functions: Parameter estimation. Applied Mathematics and Computation 219(8): 3729-3739.
5. Tanaka K (2013) Distributions of the maximum likelihood and minimum contrast estimators associated with the fractional Ornstein-Uhlenbeck process. Statistical Inference for Stochastic Processes 16(3): 173-192.
6. Bishwal JPN (2008) Parameter estimation in stochastic differential equations. Lecture notes in mathematics 1923. Springer-Verlag, Germany.