Theoretical Model and Experimental Analysis for Optical Band Gap

Chalcogenide glasses are widely studied due to their interesting physical and optical properties. Chalcogenide glasses have a wide range of applications such as phase change memory devices, optical and electrical data storage, photovoltaic solar cells, xerography, optical fibre and fiber laser. An optical property plays a significant role in most of the applications of chalcogenide glasses. Among the chalcogenide glasses, Se based glass alloys in amorphous and crystalline forms which have found numerous applications based on optical and electrical properties [1]. Chalcogenide glasses can be used to develop better understanding of the glassy state, moreover pure selenium which is known to be the only element able to give monoatomic glass [2]. Hetropolar and homopolar bond formation in glasses can create compositional disorder, so compositional studies are important to enhance the understanding of the glassy material. Furthermore, compositional dependent increasing trend of binary alloys has been discussed in terms of rigidity parameter and experimental optical band gap is compared with theoretical model.

Bulk glassy samples were prepared from high purity (5N) elemental Germanium (Ge) and Selenium (Se). Germanium and selenium chunks were crushed to powders and equivalent ratios of compositions were weight and put into pre- cleaned ampoule. Bulk glasses were prepared from melt quenching technique. Ampoule was sealed under a vacuum pressure of 10-6 Torr by a torch. The sealed ampoule was put in the thermal furnace; temperature was raised gradually in steps of 25 ℃ in every ten minutes up to 1000 ℃ and the temperature was monitored by placing a thermocouple at the ampoule position inside the furnace. Ampoule was held at this temperature for 24 hours. During the melting process the ampoule was periodically rotated thoroughly mix the alloy. After the end of 48 hours the ampoules were removed and immediately quenched in ice-water mixture to freeze the glassy structure. The ampoule was then broken to recover the glassy sample. The ingots were polished for optical measurement. Polished samples were used to record UV-Visible transmission spectra.

Glasses do not have long range order; due to lack of periodic configuration at long range order, physics of glasses is still far behind to understand the peculiar nature of the material properties. Short range order in glassy material is nearly same as those of crystalline counterpart. Chalcogenide glasses are covalent in nature and obeying the so called 8-N rule, where N is the valency of an atom. According to this rule the number of nearest neighbor atoms for selenium (Se) and Germanium (Ge) are, respectively 2 and 4. The average coordination number of covalent bonds is a good measure representing the characters of atomic units [3].

The average coordination number for a binary sample can be expressed as:

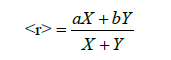
a= coordination number of Ge and b is the coordination number of Selenium then for Ge_xSe_1-x glassy sample < r>=4x+2(1-x)= 2x+2. Network dimensionality D which is defined as number of dimensions where covalently bonded clusters can be extended, according to R. Zallen [4] D =1 and 3 respectively for amorphous selenium and germanium. D =1 for selenium corresponds to chain like morphology, in which entangled chain molecules are held together with weak intermolecular forces mostly consisting of Vander Waals type, and D=3 means three dimensional continuousrandom networks.

Figure 1:Optical transmission of Ge33Se67 glass versus wavelength.

Figure 1 shows % of optical transmission as a function of wavelength for Ge₃₃Se₆₇ composition. Selenium glasses posses a transmission range from 8-12μm, but tellurium glasses offer the widest infrared transmission [5]. Figure 1 shows very good transmission 92% in UV-Visible range, no scattering or absorption in this range. The variation of (αhυ)² with photon energy hυ for the same composition is shown in Figure 2 The value of optical direct band gap has been calculated by interpolating intercept on X–axis as shown in Figure 2, same procedure has been adopted for other compositions and variation of band gap have been obtained for compositions. It is evident that the variation of optical band gap increases with increasing germanium percentage in selenium matrix up to Ge₃₃Se₆₇ compositions/average coordination number as shown in Figure 3. The compositionally induced increasing trend of band gap may be understood as follows.

Figure 2:Direct band gap analysis for Ge₃₃Se₆₇ composition.

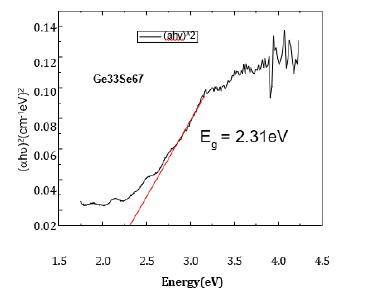
Figure 3:Variation of band gap with fitted model across GexSe1-x glass series.

E_Ge-Se = (E_Ge-Ge×E_Se-Se)^1/2+30(X_A-X_B)²;where X_A and X_B are electro negativity of Ge and Selenium. E_Ge-Se is 193.53KJ/mol based on the computation above. Since Ge-Se has the highest bond energies, Ge-Se bonds will form first. It’s been noted that this bond strategy ignores flaws like dangling bonds; these defects, along with the lesser Vander Waals forces’ contribution to bond energy, result in linkages that are weaker than ordinary covalent bonds and further stabilize the structure [7]. The alloy’s composition affects the glassy material’s optical band gap. An optical band gap determination model is presented, with the compositional dependence form being as follows:

The compositional distinctive attribute of this series, power p = 0.03, is determined from the fitted model over the series on the band gap as shown in Figure 3. On the other hand, Duffy [8] has obtained an empirical formula that relates energy gap E_g to molar refraction R_M and molar volume V_M,

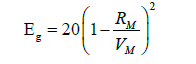
The average molar refraction of isotropic materials for glasses is provided by this equation. The polarizability, or electrons’ response to an applied field, is shown by the Lorentz-Lorentz equation. The volume (cm³/mol) parameter of the molar refraction R_M, the molar refraction R_M can be calculated as a function of polarizability α_m when Avogadro number N_A is included.

with αm in (Ǻ³), the relationship between R_M and α_m is transformed as R_M =2.52α_m.

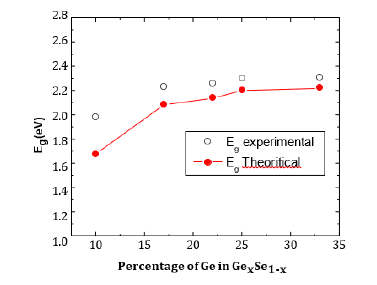
Theoretical optical band gap for Ge_xSe_1-x compositions has been computed and is displayed in Figure 4 alongside the experimental band gap; thus, the optical band gap theoretical and experimental results fairly agree. When we plotted E_g optical vs. (1-R_M/V_M), we discovered a new correlation:

Figure 4:Theoretical and experimental band gap fairly matches across Ge_xSe_1-x compositions.

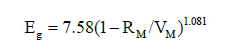
as shown in Figure (5).

Figure 5:Correlation between Eg and 1- R_M/V_M.

The number of constraint N_C is calculated according to the relation:

As the Germanium content in the Selenium matrix increases, so do the number of constraints N_C and the average coordination number < r>. An increase in network cross-linking is associated with this growth. By rising the atomic proportion of germanium, the network’s stiffness is reflected in both the average coordination number and Nc. Ge_xSe_1-x glasses are rigidly connected, where < r> > 2.4. Based on the concept of average coordination proposed by Phillips [3] and Thorpe [9] glassy network consists of mixture of floppy and rigid regions. The glass network at < r>=2.4 transform from floppy structure to rigid structure. The constraints number can be used to evaluate the cross-linking density (C_D). Values of C_D were estimated from relation [10] according to:

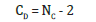
The compositional dependency of the estimated crosslinking density and density from Lorentz are presented in Figure 6. Thus, compactness (δ) is reintroduced which is a measure of normalized change in cross-linking density with the composition glass density, hence, compactness 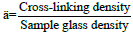quantity. Since all of the selenium is knotted with Germanium at the chemical threshold composition, there is no availability of free volume there at = 2.67 composition, as can be seen in Figure 6, which illustrates how cross-linking density increases with increasing germanium content. This indicates that the cross-linking density is a measure of rigidity in the composition. Figure 7 makes the compactness δ quite evident. Rigidity and compactness are maximal at = 2.67, where rigidity completely percolates and all selenium is consumed by the germanium. At this value, 2D layered structures are fully evolved and rigidity and compactness are maximal. Initially, at very low Germanium concentration, the network is floppy and isolated rigid regions are very small, so rigidity is very small. As the doping of Germanium concentration increases, the cross-linking increases, the free volume becomes smaller, so rigidity increases. Glasses have the highest chemical stability at < r> =2.67 because they solely contain Ge-Se bonds. Because the system is the most compact, the Ge-Se bond energies are the biggest.

Figure 6:Cross linking density and density versus average coordination number.

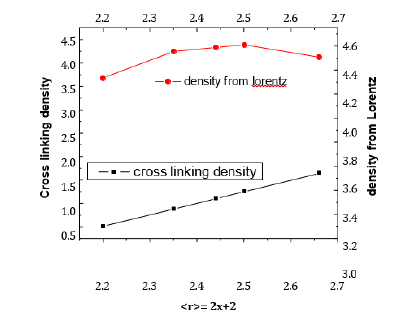
Figure 7:Modified Compactness versus compositions across GeSe series.

Optical direct band gap has been determined experimentally across the Ge_xSe_1-x compositions and theoretically band gap is estimated from Duffy’s relation which is fairly fits with the compositions. Power model is also considered which fits the band gap and it gave us power p = 0.03 over this series. A new correlation is also obtained for this glass series. We have introduced the new concept of modified compactness for covalent glasses and composition dependent are understood. We did not experimentally measured densities of the compositions, it is suggested that more elaborate studies are further necessary to measure experimental densities of the glasses.

This piece of work was performed without financial assistance, and the author has no conflicts of interest. The author is not a research competitor.

1. Srivastava S, Mehta N, Twirai RS, Shukla RK, Kumar A (2011) Chemical bond approach to optical band gap in Se100-xSbx chalcogenide glasses. J Optoelecron Adv Mater 13(1): 13.
2. Winter A, Verress (1982) Refractaires 36: 259.
3. Phillips JC (1979) Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J Non-Cryst Solids 34(2): 153.
4. Zallen R (1983) The physics of amorphous solids, Wiley, New York,
5. Venugopal K, Bhatnagar AK (1992) J Phys D: Appl Phys 25:
6. Pauling LJ (1932) Am Chem Soc 54: 5370.
7. Othman AA, Aly KA, Abousehly AM (2007) Thin Solid Films 515:
8. Duffy JA (1986) Solid State Chem 62: 145.
9. Thorpe MF (1983) J Non-Cryst Solids 57(3): 355.
10. Faud S (2001) Phys B 293(3-4): 276.