Modified Genetic Algorithm to Obtain Optimum Shape Design using Image Processing and Computational Fluid Dynamic for Parallel Computation

Mankind has always sought to find answers to the vague questions of physical and natural phenomena in very large dimensions or on very small scales. Researchers have always done a lot of research to clarify ambiguous issues. Experimental, analytical and numerical methods are always being developed to increase the accuracy of simulation or research. One of the most efficient ways in research, which is referred to as an equipped laboratory, is a numerical method for simulating any physical phenomenon. In numerical methods, there is always an attempt to increase the simulation accuracy by removing simplifying assumptions on the governing equations and also developing the algorithm to create strong numerical couplings and increase the convergence rate. To achieve such accuracy and ensure the obtained answer, the computational costs in terms of time and the cost of computing machines are extremely important. The development of different algorithms in order to discretize mathematical equations into the algebraic mode for the understanding of the computing machine, as well as the creation of strong multi-way couplings, lead to reducing the calculation time. But still, to perform such calculations, a computing machine is needed that can create desirable performances.

With the ever-increasing development of hardware components such as the computing core and internal memory of computers, users have access to faster computing speeds. Such improvements are very desirable for simple home users to carry out simple educational or academic projects, while it is practically impossible to carry out important industrial projects with such systems. Because in such research, many effective parameters must be checked on the problem. Therefore, it will take months or sometimes years with a single computer. Also, buying supercomputers that have many computing cores and a lot of memory is very expensive and often unavailable. One of the most efficient tasks is to connect several common computers. With this, it used all the performance of the connected hardware as a very strong system and performed the necessary executions on all the computing cores in parallel, which is called parallel processing. This method is very economical both in terms of cost and calculation time. Parallel processing is an effective method for solving engineering problems, especially in computational fluid dynamics, where fluid behavior as well as heat and mass transfer are simulated and studied [1-4]. In a systemic approach, in order to obtain an optimal output or outputs, all input parameters to the system should be analyzed exponentially.

This causes the number of examined test cases to increase and with the help of parallel processing, the desired and optimal result can be found more quickly [5-8]. The genetic algorithm as an efficient method in optimization problems has always been of interest to researchers. This algorithm is used in various engineering topics, especially fluid mechanics engineering [1,9-12]. In the numerical method, dividing the computational field into a finite element or finite volume, which is known as mesh generation, is a big challenge for researchers in different geometries and multiple flow fields. Various methods have been developed to produce mesh on the field. Today, with the advancement of artificial intelligence and its related branches, various algorithms and methods have been developed with high precision [13-16]. One of the new methods that are able to generate a mesh with acceptable accuracy is the image processing method [17-20]. The development of smartphones with powerful cameras has led to the fact that today all users can easily take digital photos and share them with high quality. For this reason, simple users can easily produce their desired mesh in the computing field with the help of image processing in the technical and engineering space to complete their projects without any trouble, spending time and additional training.

The combination of image processing with a genetic algorithm in solving fluid problems is a new method in simulation, which is extremely economical in terms of time and computational cost and can determine the optimal solution of the investigated system [21- 25]. This method requires parallel processing in industrial projects that require detailed checks with a high number, which is the goal of the upcoming research. According to the studies conducted, the author believes that until now there is no such study on solving problems by combining image processing, genetic algorithm and computational fluid dynamics. At the beginning of the study road, image processing to staggered a moving mesh on a square in turbulent flow was described. Abolpour et al. [26] simulated a turbulent fluid flow around a square obstacle as a bluff body using a developed homemade code in the MATLAB software by simultaneously solving the continuity, Navier-Stokes and k-ɛ turbulent model equations. Their study’s main novelty is edge detection bluff body using the image processing method. After detecting the edges of the square obstacle, an orthogonal, structured and staggered mesh is generated for this flow field.

The usage of the image processing method with the genetic algorithm in CFD applications has been presented in the reference [21,23] as a first test case. A multi-objective optimal design has been presented to increase the heat transfer rate and low-pressure drop in a two-dimensional baffle heat exchanger considering turbulent fluid flow in a channel in mentioned reference. They utilized a genetic algorithm for obtaining an optimum arrangement of two flat-plate for satisfying mentioned purposes. Also, the image processing method has been used for detecting the edges of the mounted baffles and the appropriate mesh configuration has been generated for the solution domain. As a second test case, Abolpour et al. [24] presented an optimal design for high mixing index and low-pressure drop in a two-dimensional Tesla-shaped micromixer with a laminar fluid flow regime. The genetic algorithm is used for obtaining optimum structural design and the image processing method has been utilized to identify the edges of the micromixer in order to generate mesh configuration over the computational field. The optimum design of the micromixer structure has been obtained by rotating central obstacles of a Tesla micromixer with an optimum value of mixing cost, which is a function of two target parameters.

>The results showed that the optimum design has a lower mixing cost than the original type of Tesla micromixer. The third study of the combination of genetic algorithms and image-processing methods is related to the optimal design for the highest possible particle-trapping rate in a turbulent fluid that flows over filters in a rectangular channel [22]. The new configuration of the filters investigates increasing the performance of the particle trapping rate. The comparison between simple and optimized filter locations shows that escaped particles reduce by 23% in the optimized condition. Abolpour et al. [25] studied the shape optimization approach based on the binary genetic algorithm coupled with the image processing method for drag reduction purposes. A system-specified code in MATLAB software has been developed to find the optimized configuration. The combination of genetic algorithm with image processing in two other physical problems is in progress and is being prepared for publication by the author. In the first study, an optimal combination of nanoparticles in the fluid flow to increase heat transfer with the lowest pressure drop in a heat exchanger has been investigated. The author believes that, according to the review of the articles, there is no optimal way to combine several nanoparticles.

In the next research, the issue of water desalination has been investigated. Investigating the movement of ions in saltwater and seawater, as well as its diversion and elimination, has been done accurately in a modified channel and is under follow-up for publication. To increase the accuracy in the simulations and produce a more accurate mesh, it is necessary to increase the number of pixels in the digital photo. This increase greatly increases the time and cost of calculations, so the strong need for parallel processing is essential which is the main aim of the present study.

In this research, the modified genetic algorithm which has been developed by the author is combined with image processing and computational fluid dynamics for parallel processing. The developed algorithm has the possibility of simulating physical phenomena with mass and heat transfer in a laminar and turbulent flow. The image processing method has been used to produce the computational mesh. It is done by importing a digital photo in grayscale and converting it to a black-and-white photo with strong color contrast by the filters applied in the image processing method. This work leads to the identification of the edges of the object and the desired mesh is created in a movable way. Complete explanations along with the examination of image processing methods in various fluid dynamics problems are given in references [21-25]. Figure 1 shows the general flowchart of the existing steps until reaching the optimal solution. The main computer, which is responsible for controlling sub-computers in parallel processing, produces the first generation of inputs for the desired problem with the help of the genetic algorithm.

Figure 1:The flowchart of the process steps.

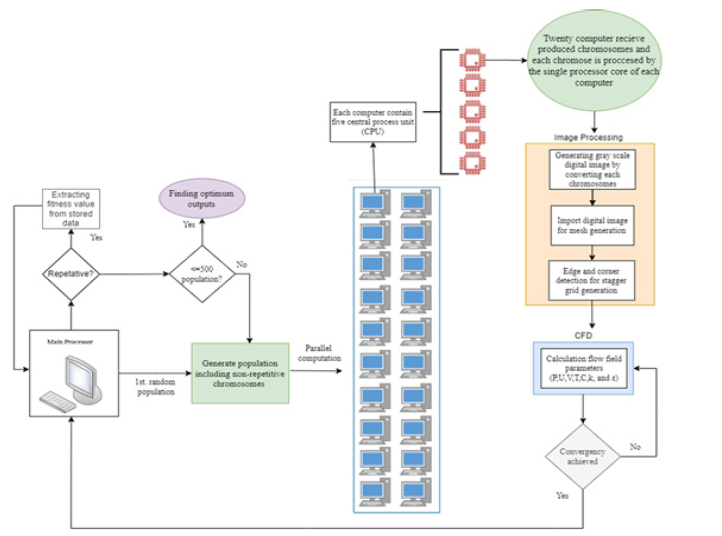
The first generation produced, which has a set of chromosomes, is divided among twenty computers that are responsible for image processing and numerical calculations. Every existing computer has five CPU cores; each core takes one chromosome as a test case for a run. After processing the image and solving the current in the entire field, the current parameters are obtained. The goal of the problem, the parameter that has been studied for optimization, is calculated and stored. All optimization information is stored in the central computer and a database is produced. At this stage, the new generation is produced and the absence of duplicate chromosomes is applied as a filter. This leads to the reduction of generation time in the genetic algorithm stage. According to the type of problem under investigation, restrictions are applied in the application of the genetic algorithm, which leads to a significant reduction in the time of solving the problem, which will be explained in the following sections. As mentioned earlier, in the current study, a modified genetic algorithm was used and the relevant flowchart is shown in Figure 2. The modified algorithm compared to the normal case is that a dominant chromosome is also applied at the time of parent selection. This dominant chromosome, called the master chromosome, is the best found. The effect of this chromosome in the production of the next generations is to obtain a solution close to this dominant chromosome but in an optimal state.

Figure 2:The flowchart of the modified genetic algorithm.

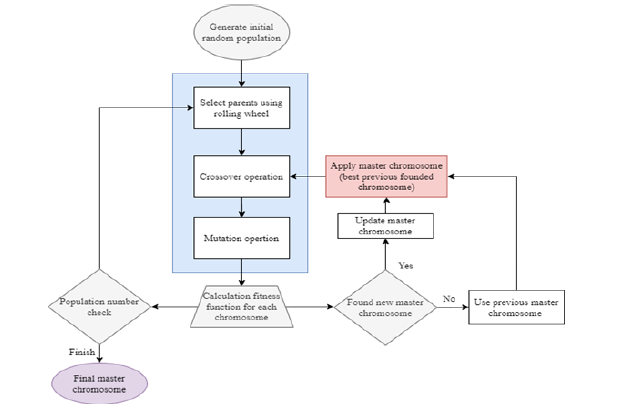
According to Figure 2, when the crossover step is applied, this chromosome is also involved. With the acquisition of new chromosomes, the objective function is investigated. If a new chromosome is obtained that is optimal compared to the master chromosome, that chromosome replaces the master chromosome and is used in the production of new generations. In the case of a normal genetic algorithm, this step does not exist and the number of random chromosomes created will be far from the desired optimal solution. This applied modification helps the obtained chromosomes to move faster than the optimization goal. Genetically, this type of mutation is seen in nature in cats. The author believes that according to the experiments, the described algorithm is much more efficient than the traditional genetic algorithms.

According to the mentioned references [21-26], the combination of genetic algorithm with image processing can be verified in solving computational fluid dynamics problems for phenomena that have thermo-hydrodynamic fields along with concentration fields in laminar and turbulent flow fields that may have heat and mass transfer. Also, in the Lagrangian approach, the tracking of particles in the flow field (such as nanoparticles or ions suspended in the fluid) can be simulated. The equations governing the flow field to simulate the stated physical phenomena are expressed as follows. Chien’s et al. [27] low Reynolds k-ε model [27,28], Launder et al. [29], Franke et al. [30], Kato et al. [31,32] and Boussinesq approximation [33] have been used to model this incompressible turbulent fluid flow. The steady-state governing equations for the fluid [27-33] and heat [34] flows have been illustrated as follows according to Einstein’s notation, which has been solved concurrently:

To determine particle positions, the Lagrangian particle track approach was used. The acceleration of each particle is obtained as follows:

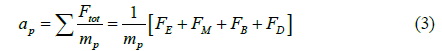
The total force that pushes the particles is defined as follows as the electrical force (F_E), a magnetic force (F_M) known as Lorenz force, Brownian force (F_B) and drag force(F_D) respectively;

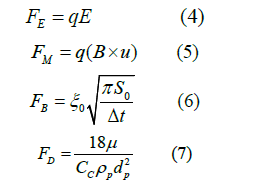
Which q is the ion charge (for an ion 1+: q =1.6×10⁻¹⁹C ), E is the electric field (V/m or N/C), B is the magnetic field (N.s/C.m) and u is the axial velocity (m/s) along the x-axis respectively. Cunningham’s correction to Stokes drags law and Spectral intensity in equations (6) and (7) has been defined as [33]:

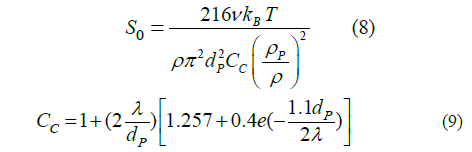
The magnetic and electrical force acted on dissolved charged ions in the domain. The total force on the particles can be evaluated as;

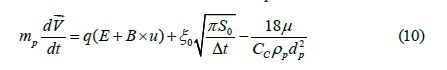
Where V is the two-dimensional velocity vector (V = ui + vj). The double integration of equation (10) evaluates the coordinate of each particle in the flow field. After calculating the velocity field by computational fluid dynamics, a one-way coupling relationship is established between the velocity field (u) and the position of the particles (∫∫dV/dt). The segregate algorithm has been considered to determine the momentum of each particle. Equations (1) to (7) only show that it applies to the problem in question in the model presented by the author and not all equations were used in the test case.

Test case

To check the effectiveness of the current research in parallel processing, we are investigating the optimization of a simple square to reduce the drag force. Figure 3 shows the number of pixels in a square. Each square is introduced as a gene in the genetic algorithm. It shows the total set of genes in the form of a chromosome. The right column in the figure shown in black is fixed and is considered a constraint applied by us in the genetic algorithm. For greater simplicity and time reduction in the implementation of the developed code, the symmetry condition is applied. Figure 3 shows the top view, therefore, the genes on one side of the symmetry line are used for simulation. In the genetic algorithm, each gene has a value of 0 or 1, which means that the desired pixel is on or off. This means that the blackness of each pixel means a solid body and the whiteness of a pixel means a flow field. Another condition that is considered in the genetic algorithm is the condition of continuity in the shape obtained from each chromosome. The central computer controls the output of each computer in the parallel processor. If the obtained shape does not have pixel continuity (for example, several genes are lighted in a scattered manner), it is not acceptable and will be removed. This condition helps significantly in removing extra chromosomes and reduces the execution time.

Figure 3:The consideration of genes for chromosomes in the genetic algorithm for the test case.

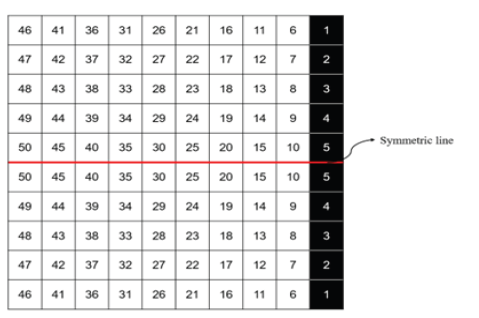
The three conditions of symmetry, non-repetition and chromosome continuity are the conditions used in the modified genetic algorithm. Validation and study of the network impression and time step in the solution are omitted and the reader can access the full details in references [21-26]. The boundary conditions considered in the current research for testing someone are as follows:

At the inlet (x = 0) , uniform velocity, kinetic and dissipation rate distribution, have been concerned. In addition, a constant pressure gradient along the x-axis has been taken into use.

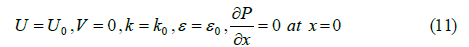
At the outlet (x = L) , the gradient of V velocity along the y-axis and the gradient of variables along the x-axis are considered zero.

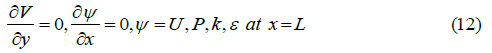
On the wall sides of the obstacle, no-slip and no penetration (U_wall = 0,V_wall= 0) and at the top and bottom of the computational field, the open boundary conditions 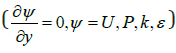have been implemented [35].

In the present study, the developed system-specified code detects the downstream area behind the inserted obstacle and sets all velocity values to zero as an initial value to run the calculation, automatically. This step increases the convergence rate and decreases the computation cost. The inlet velocity has been chosen U_inlet=0.535m/s , based on Lyn et al. [36] and 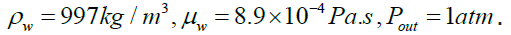. The inlet turbulent kinetic energy 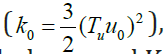, was calculated from the equation of the isotropic turbulence and Kolmogorov expression has been used for the dissipation term 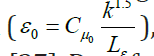, which was extracted from the eddy- viscosity relation [37]. Drag force is calculated by velocity values at the outlet and inlet for each generated shape. For incompressible flow, the drag force coefficient is estimated by the following relation [38]:

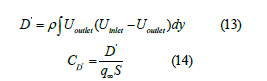
The drag coefficient of the population in the binary genetic algorithm has been calculated after the image processing step and each drag value was saved for comparison as a fitness function [39].

Figure 4:Predictions of the developed computational fluid dynamic for the initial shape, a) velocity vectors (u_in=0.535m.sec^-1), b) temperature contours (T_in=300K and T_Body=350K) and c) particles trajectory (d_p=100nm).

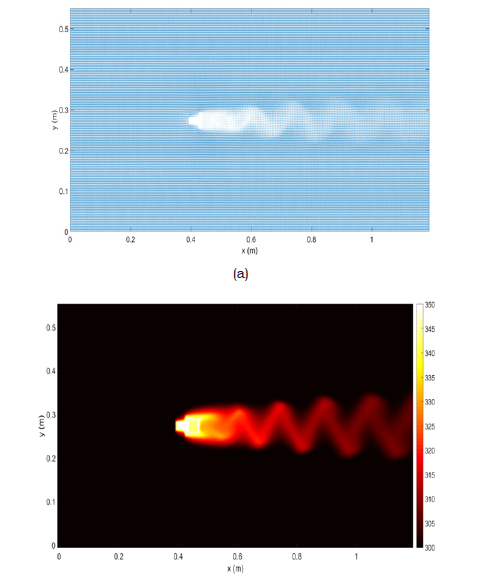
The ability of optimization and also the model numerical predictions for the fluid flow and heat and mass transfers of the present method for a combination of genetic algorithm, image processing and computational fluid dynamic have been validated previously [21-26]. For approving the ability of the presented method in this study, a case study (i.e., obtaining a two-dimensional shape with a minimum drag coefficient in a fluid flow field) with a high calculation time requirement has been presented. The grid independency study of the developed computational fluid dynamic code for this case has been presented in our previous study [25]. Therefore, in this study, our focus is on the performance of a modified parallel genetic algorithm for solving high-time required calculations for obtaining optimum geometries for different optimization targets using the presented method for coupled computational fluid dynamics, genetic algorithm and image processing. As previously mentioned, the presented modified version of the genetic algorithm can find local optimum shape design based on an initially defined geometry. The initial shape has been chosen from our previous study and Figure 4 presents the predictions of the developed computational fluid dynamics for this shape. This Figure has been presented for illustrating some of the computational fluid dynamic abilities of the developed code. Therefore, each one (or multiple combinations) of the fluid, heat or mass flow quantities can be optimized using this method [21-26].

However, a certain case study has been presented for a parallel optimization process based on the developed modified genetic algorithm in this study. In this case, we tried to minimize the entered drag force to the presented initial case in Figure 4 by obtaining the local optimum geometry similar to this shape. Attending to the presented modified parallel genetic algorithm in this study, this initial shape has been defined as one of the triple parents (i.e. as a master parent) of the generated chromosomes in the initial population of this algorithm. Therefore, the modified optimization process optimized this shape for minimizing its drag coefficient by increasing or adding pixels to different sections of it, step by step. Figure 5 shows the average and the best drag coefficients of different populations in 500 iterations of the developed modified version of the genetic algorithm. As shown in this Figure, the 0th population of this modified genetic algorithm is the defined initial shape, which was the master parent of the generated semi-random chromosomes in the 1st population of this algorithm. Therefore, it is clear that the generated chromosomes in this population were generated based on this initial shape. Other populations were generated based on the described modified genetic algorithm (i.e. triple parent method) by the presence of the best-founded shape as the master parent of the next populations. After these 500 optimization iterations, the final master chromosome is the best-found solution for this problem.

Figure 5:Average and the best (master) drag coefficients of different populations in 500 iterations of the modified genetic algorithm.

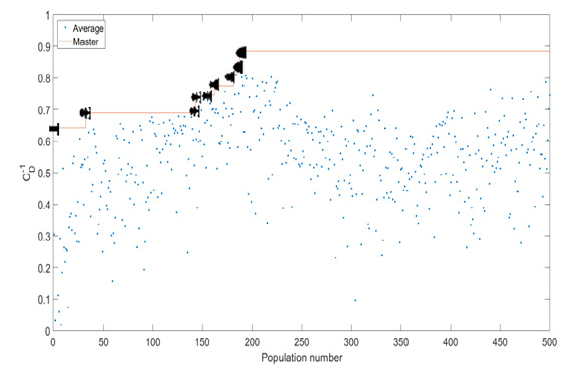
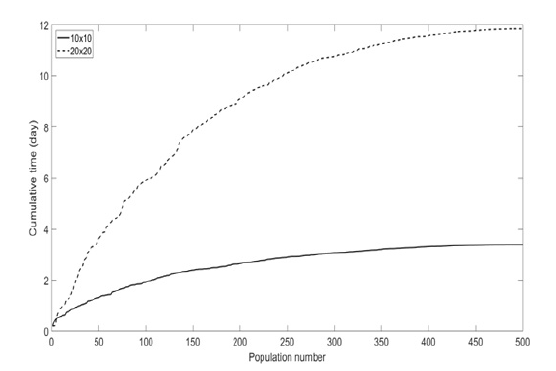
Figure 6 shows the velocity vectors, temperature contour and particle trajectory around the obtained optimum design in this study. The results from comparing this figure with the model predictions in Figure 4 indicate that the stagnation zone in front of the optimized shape is smaller than the initial shape; therefore, the momentum dissipation and also the entered drag force are decreased for this optimized shape. This improvement in the aerodynamic of the shape (from C_D-Initial=1.56 to C_D-Final=1.13) decreased its particle trapping from 2.97% for the initial shape to 1.22% for the optimized shape. The effects of this optimization on the temperature gradient in the passing fluid flow field are obvious in this comparison. Increasing the complexity of the geometry by increasing the size of genetic algorithm chromosomes (i.e., number of genes) and increasing the required calculation time (for the computational flu id dynamic meshing size and also the genetic algorithm necessary population size) highlights the importance of the presented method for parallel computing. For approving this ability, a case with the same boundary conditions and higher chromosome size (i.e., a 20×20 shape), has been optimized and its optimization calculation time has been compared with the 10×10 case. As shown in Figure 7, increasing the size of the calculation by increasing the chromosome size is considerable, but still is acceptable for a fast numerical solution, attending to the complexity of the problem.

Figure 6:Predictions of the developed computational fluid dynamics for the optimum shape, a) velocity vectors (u_in=0.535m.sec-1), b) temperature contours (T_in=300K and T_Body=350K) and c) particles trajectory (d_p=100nm).

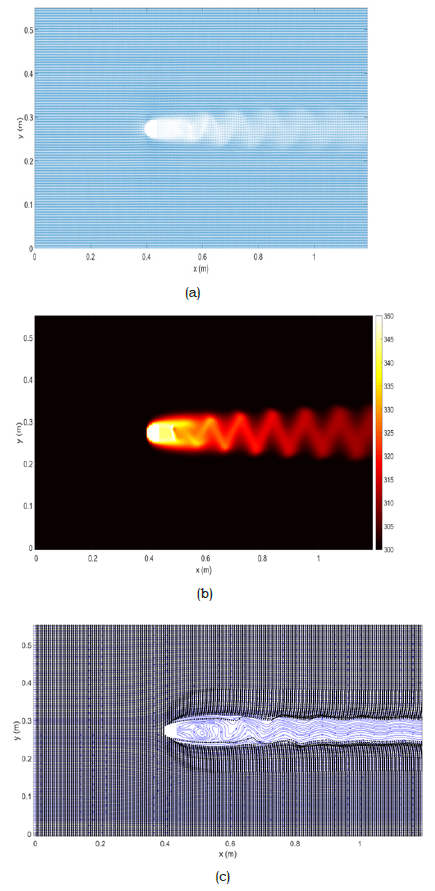
Figure 7:Calculation time for 10×10 and 20×20 cases.

In this study, a combination of the modified parallel genetic algorithm, image processing and computational fluid dynamic was presented for obtaining optimum shapes for different multi-objective targets. A homemade MATLAB code was developed to find the optimized shape considering different transport phenomena targets. The main purpose of this study was to develop a modified parallel genetic algorithm for numerical solving of high calculation cost optimizations in the fluid mechanic fields. A case study was presented for illustrating the ability of this method for utilizing a network of computer cores for parallel optimization of high-time-consuming computational fluid dynamics-based optimizations. In this case, a certain shape optimization was investigated for minimizing the entered drag force to it by a passing fluid flow. After 500 iterations, the optimized shape in the 188th iteration was found and the drag coefficient is about 1.13, which is an acceptable value comparing the initial shape drag coefficient which was equal to 1.56.

The authors declare that they have no conflict of interest.

No funding was received to assist with the preparation of this manuscript.

This article does not contain any studies with human participants or animals performed by any of the authors.

Code and data for replication can be provided upon request.

1. Houzeaux G, Badia RM, Borrell R, Dosimont D, Ejarque J, et al. (2022) Dynamic resource allocation for efficient parallel CFD simulations. Computers & Fluids 245: 105577.
2. Lai J, Li H, Tian Z (2018) CPU/GPU heterogeneous parallel CFD solver and optimizations. Proceedings of the 2018 International Conference on Service Robotics Technologies, pp. 88-92.
3. Wang YX, Zhang LL, Liu W, Xiang HC, Yu Z, et al. (2018) Performance optimizations for scalable CFD applications on hybrid CPU+MIC heterogeneous computing system with millions of cores. Computers & Fluids 173: 226-236.
4. Zhang X, Guo X, Weng Y, Zhang X, Lu X, et al. (2023) Hybrid MPI and CUDA paralleled finite volume unstructured CFD simulations on a multi-GPU system. Future Generation Computer Systems 139: 1-16.
5. Lin X, Wu Y (2020) Parameters identification of photovoltaic models using niche-based particle swarm optimization in parallel computing architecture. Energy 196: 117054.
6. Prihozhy A (2019) Analysis, transformation and optimization for high performance parallel computing. BNTU, Minsk, Minskaja voblasć, Belarus, p. 229.
7. Rashid ZN, Subhi RM, Sharif KH, Kaewan J (2018) Distributed cloud computing and distributed parallel computing: A review. 2018 International Conference on Advanced Science and Engineering (ICOASE), Duhok, Kurdistan Region, Iraq.
8. Xing J, Luo Y, Gao Z (2020) A global optimization strategy based on the kriging surrogate model and parallel computing. Structural and Multidisciplinary Optimization 62(1): 405-417.
9. Ge Y, He Q, Lin Y, Yuan W, Chen J, et al. (2022) Multi-objective optimization of a mini-channel heat sink with non-uniform fins using genetic algorithm in coupling with CFD models. Applied Thermal Engineering 207: 118127.
10. Ghadimi B, Amir N, Ahmad SN, Nasim N (2019) Shape optimization of a centrifugal blood pump by coupling CFD with metamodel-assisted genetic algorithm. Journal of Artificial Organs 22(1): 29-36.
11. He Z, Yan Y, Feng S, Yang Z, Li Z, et al. (2021) Multi-objective optimizations on thermal and hydraulic performance of symmetric and asymmetric bionic Y-shaped fractal networks by genetic algorithm coupled with CFD simulation. International Communications in Heat and Mass Transfer 124: 105261.
12. Kaseb Z, Rahbar M (2022) Towards CFD-based optimization of urban wind conditions: Comparison of genetic algorithm, particle swarm optimization and a hybrid algorithm. Sustainable Cities and Society 77: 103565.
13. Chen W, Zheng X, Ke J, Na L, Luo Z, et al. (2019) Quadrilateral mesh generation I: Metric based method. Computer Methods in Applied Mechanics and Engineering 356: 652-668.
14. Chen X, Li T, Wan Q, He X, Gong C, et al. (2022) MGNet: A novel differential mesh generation method based on unsupervised neural networks. Engineering with Computers 38(5): 4409-4421.
15. Schneider T, Panozzo D, Zhou X (2021) Isogeometric high order mesh generation. Computer Methods in Applied Mechanics and Engineering 386: 114104.
16. Zhang Z, Wang Y, Peter KJ, He W (2020) MeshingNet: A new mesh generation method based on deep learning. International Conference on Computational Science, pp. 186-198.
17. Dai A, Nießner M (2019) Scan2mesh: From unstructured range scans to 3D meshes. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5569-5578.
18. Nanduri JR, Pino RF, Celik I (2009) CFD mesh generation for biological flows: Geometry reconstruction using diagnostic images. Computers & Fluids 38(5): 1026-1032.
19. Nie Y, Han X, Guo S, Zheng Y, Jian C, et al. (2020) Total3Dunderstanding: Joint layout, object pose and mesh reconstruction for indoor scenes from a single image. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, Washington, USA.
20. Zhang Y (2016) Geometric modeling and mesh generation from scanned images. Chapman and Hall/CRC, Boca Raton, Florida, USA, p. 364.
21. Abolpour B, Hekmatkhah R, Ansari AB (2023) The smart design of heat exchangers with expanded surfaces by genetic algorithm and image processing. Sharif Journal of Mechanical Engineering 39(2): 25-35.
22. Abolpour B, Hekmatkhah R, Shamsoddini R (2022) Multi-objective optimization of the particle trapping enhancement by genetic algorithm and image processing method. SSRN 4201181 p. 33.
23. Abolpour B, Hekmatkhah R, Shamsoddini R (2021) Multi-objective optimum design for double baffle heat exchangers. Thermal Science and Engineering Progress 26(1): 101132.
24. Abolpour B, Hekmatkhah R, Shamsoddini R (2022) Optimum design for the tesla micromixer. Microfluidics and Nanofluidics 26(6): 1-8.
25. Abolpour B, Hekmatkhah R, Shamsoddini R (2022) A novel approach for obtaining optimum shape design with the minimum drag coefficient. Structural and Multidisciplinary Optimization 65(11): 1-16.
26. Abolpour B, Rahim S (2022) Modelling of turbulent flow around a square obstacle using a generated mesh by the image processing method. International Journal of Advanced Design and Manufacturing Technology 15(4): 113-123.
27. Chien KY (1982) Predictions of channel and boundary-layer flows with a low-Reynolds-number turbulence model. AIAA Journal 20(1): 33-38.
28. Patel VC, Rodi W, Scheuerer G (1985) Turbulence models for near-wall and low Reynolds number flows-a review. AIAA Journal 23(9): 1308-1319.
29. Launder BE, Spalding DB (1983) The numerical computation of turbulent flows. Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion, pp. 96-116.
30. Franke R, Rodi W (1993) Calculation of vortex shedding past a square cylinder with various turbulence models. Turbulent Shear Flows 8, pp. 189-204.
31. Kato M (1993) The modelling of turbulent flow around stationary and vibrating square cylinders. Turbulent Shear Flow 1, pp. 1-6.
32. Launder BE, Sandham DB (2002) Closure strategies for turbulent and transitional flows. Cambridge University Press, Cambridge, UK.
33. Abolpour B, Mehdi AM, Soltani AG, Mehdi A (2017) Study of the motion and deposition of micro particles in a vertical tube containing uniform gas flow. Heat and Mass Transfer 53(12): 3517-3528.
34. Aslan E, Taymaz I, Islamoglu Y (2016) Finite volume simulation for convective heat transfer in wavy channels. Heat and Mass Transfer 52(3): 483-497.
35. Grinstein FF (1994) Open boundary conditions in the simulation of subsonic turbulent shear flows. Journal of Computational Physics 115(1): 43-55.
36. Lyn DA, Einav S, Rodi W, Park JH (1995) A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. Journal of Fluid Mechanics 304: 285-319.
37. Younis B, Przulj VP (2006) Computation of turbulent vortex shedding. Computational Mechanics 37(5): 408-425.
38. Anderson JD (2010) Fundamentals of aerodynamics. (7^th edn), Tata McGraw-Hill Education, New York, USA.
39. Hamdia KM, Zhuang X, Rabczuk T (2021) An efficient optimization approach for designing machine learning models based on genetic algorithm. Neural Computing and Applications 33(6): 1923-1933.