- Submissions

Full Text
Strategies in Accounting and Management
Laws of Dahlquist in Multistep Methods and Some of their Modification
Imanova Mehriban1,3 and Vagif Ibrahimov2,3*
1Science Development Foundation under the President of the Republic of Azerbaijan, Baku, Azerbaijan
2Chief of the Department of Computational Mathematics, Baku State University, Baku, Azerbaijan
3Institute of Control Systems, Azerbaijan National Academy of Sciences, Baku, Azerbaijan
*Corresponding author:Vagif Ibrahimov, Chief of the Department of Computational Mathematics, Baku State University, Institute of Control Systems, Azerbaijan National Academy of Sciences, Baku, Azerbaijan
Submission:October 25, 2024;Published: November 08, 2024

ISSN:2770-6648Volume5 Issue 2
Abstract
No one doubts the relevance Multistep Methods with constant coefficients and their applications to solve different problems of Natural science. The base search for these methods was carried out by the Dahlquist. Based on this, here the description of some development of these theories and the application to solve Ordinary Differentia the Volterra Integral and the Volterra Integro-Differential Equations. Here, investigated advanced (forward-jumping) methods, and comprised the results receiving for the advanced method with the Dahlquist results. Here, have investigated the second derivative multistep methods of advanced type and shown that stable methods of advanced methods are more exact. In addition, fined the maximum value for the degree of the advanced method. Constructed methods the illustrated receiving results.
Keywords:Initial-value problem; Ordinary differential equation; The volterra integro-differential equation; Stability and degree; Multistep multiderivative methods
Introduction
As is known in the middle ages, scientists began to study the trajectory of celestial bodies, which is usually presented as the initial-value problem for Ordinary Differential Equations. Thus, solving the above noted problem, arrives the necessity to use some numerical methods. Some authors have used the power series method for solving the named problem. L. Leonid Euler shows some disadvantages of these methods. Therefore, L. Euler constructed the new method for solving above named problems. As is known, the more general numerical methods have been constructed by Adams-Morlton and Adams-Bashforth. To illustrate the above statement, let us consider the following problem (see for example [1-11]):
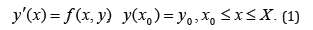
Here, suppose that, this problem has the unit continuous solution y(x), which is defined in the segment [x0,X]. And continuous to totality of arguments function f(x,y) has been defined in some closed set, in which has the continuous partial derivatives to some p, inclusively. As was noted above, the aim of this investigation is finding the numerical solution of the problem (1). Therefore, at the point xi, the exact value of the solution of the problem (1) have defined by the y(xi) and the corresponding approximately values by the y (i 0,1,2,..,N) i = . Mesh-points xi=(i 0,1,.,N) are defended as the xi+1=xi+h(i=0,1,...,N-1) . Here constant h-is the stepsize, which divides a segment [x0,X] into N equal parts. Let us but the f define the values f (xi,yi) (i=0,1,..,N).
Noted that Euler’s method can be receive from the Adams’s method as the partial case. Specialists involved in the construction and application of numerical methods to solve problem (1), generalized started all known numerical method. As the result of that the following methods were received:
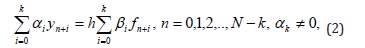
In applying this method to solving some problems of type (1), arises the question about convergence of this method. In the [1] work [12,13] has been investigated this question and proved that for the convergence of the method (2), the roots of the polynomial

must located in the unit circle on the boundary of which there is not a multiply root. This condition is called as the conception of dispersion. In the work [2], this condition is taken as the stability of the method (2). And here, have been proved that if βk= 0 and method (2) is stable. Then p ≤ k for the k ≤10. Here p-is the accuracy degree of the method (2). Noted that method (2) has been investigated by many authors, but fundamentally investigated by Dahlquist. Dahlquist for the study method (2), has used the conception of stability and degree, which was fined as follows:
Definition 1
The method (2) is called as the stable, if the roots of the polynomial ρ (λ) located in the unit circle on the boundary of which there is not multiply root.
Definition 2
The integer p is called as the degree of the method (2), if the following asymptotic equalities take place,
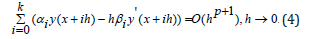
He has defined the natural conditions improved on the
coefficients of the method (2).
A. The coefficients αj,βj(j=0,1,2,..,k-m; i=0,1,..,k) are some real numbers and αk-m≠ 0.
B. The characteristic polynomials
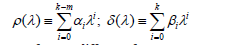
don’t have common factors different from constant.
C. The conditions ρ (1) = 0; ρ ′(1) = δ (1) are hold.
Theorem 1
If method (2) is stable and has the degree of p, then
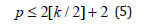
and for the each k, there are stable methods of type (2), with the degree pmax=2[k/2]+2.
From the ratios (5) receive that the degree of method (2) is bounded. To increase the accuracy of the numerical methods, in the work [10] has been recommended to use the following method:
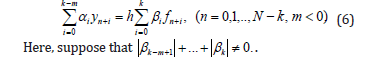
Method (6) usually is called as the advanced or forward jumping method. It is obvious that, the class of methods (2) and (6) is different from each other. The next paragraph is dedicated to the study of advanced methods.
The investigation of advanced methods
The advanced methods were constructed in the beginning of
XX century by Kowell (see for example [11-13]). Therefore, some
authors called method (6) the Kowell method. Method (6) fully
(fundamentally) has been investigated in the works (). By using the
conditions m > 0 and 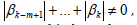 receive that the class
of method (6) is separate and independent from the method (2).
Therefore, has been found the necessary conditions imposed on the
coefficients of the method (6), which can be presented as following.
Noted that methods of type advanced have been constructed by the
famous scientists such as Laplas, Steklov, Klero, Kowelland etc. in the
work [] have been constructed the concert method with the degree
p=5 for the k=3. By the Dahlquist’s results, receive that in the class
of Multistep Method (2) there is not stable method with degree
p=k+2 for the k = 2ν −1(odd) value. By the simple comparison, the
class methods (2) and (6) receive that stable methods of type (6)
are more exact than the methods of type (2). For the comparison of
the exactness of methods (2) and (6), let us consider the following
theorem [14-18].
receive that the class
of method (6) is separate and independent from the method (2).
Therefore, has been found the necessary conditions imposed on the
coefficients of the method (6), which can be presented as following.
Noted that methods of type advanced have been constructed by the
famous scientists such as Laplas, Steklov, Klero, Kowelland etc. in the
work [] have been constructed the concert method with the degree
p=5 for the k=3. By the Dahlquist’s results, receive that in the class
of Multistep Method (2) there is not stable method with degree
p=k+2 for the k = 2ν −1(odd) value. By the simple comparison, the
class methods (2) and (6) receive that stable methods of type (6)
are more exact than the methods of type (2). For the comparison of
the exactness of methods (2) and (6), let us consider the following
theorem [14-18].
Theorem 2
If the method (6) is stable and has the degree of p, then the following takes place: p ≤ k + m +1 (k ≥ 3m). As follows from here, the method (6) is more promising. Sometimes we come across such applied problems in the solution of which there is a need to use more accurate methods. Therefore, here is considered the construction of more exact numerical method for solving problem (1). And for this aim, Euler proposed calculations of the subsequent members of the Taylor series. For the construction more exact numerical methods for solving problem (1), Dahlquist suggest the following method (see for example [11-13],[19]):
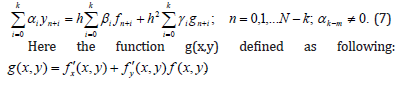
Dahlquist fundamentally investigated this method and prove some theorems. The main result of the named work can be presented as following.
Theorem 3
Suppose that method of (7) is stable and has the degree of p, then
For the each k, there exists stable method of type (7) with the degree of p = 2k + 2 .
To increase the accuracy of the method (7), in [12] the method (7) has been modified as the following form:

Method (7) can be received from the method (9) the as partial case.
The method fully explored in the work [18]. Note that the case max(l, s) ≤ k − m, investigated by Dahlquist. Therefore, here consider to investigation the method (9) in the case max(l, s) > k − m. Let us consider the definition of the maximum order of accuracy for the method (9) in the case max(l, s) > k − m.
Theorem 4
If method (9) has degree of p and stable in the case max(l, s) > k − m, then there are stable methods of type (9) with the degree pmax= l + s + m +2 (k ≥ 3m). Note that if in the method (7) the coefficients (i 0,1,.., k) i β = satisfy the condition βi=(i=0,1,..,k) then the definition of stability changes dramatically [20-39]. In this case, the conception stability can be define as the following:
Definition 3
Method (7) called as the stable in the case βi=(i=0,1,..,k)
, if the rots of the polynomial  located in the unit circle
on the boundary of which there is not multiply roots with the
exception of the double root λ =1.
located in the unit circle
on the boundary of which there is not multiply roots with the
exception of the double root λ =1.
For the illustration of the results given above let us to consider the following methods of type (9):
By the simple comparison, receive that the properties of these methods are subject to the above-obtained results of the law. The similarly results one can be fined in the works (see for example [40- 49]).
Numerical Results
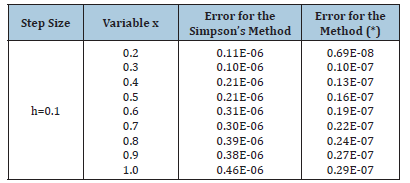
For the illustration of the results about the contraction the new way to receive more that result, let us applied method of type (2) to solve following very simple problem:

For solving this example, let us to use the following Simpson method:

and the following Simpson method with the step-size
Results receiving for these methods have tabulated in the Table 1.
Table 1:Results for the step size h: =0.1
Conclusion
Here consider a comparison of some results for Multistep Methods with the constant coefficients using first and second derivatives solutions to the problem (1). Have shown that, there are some class of methods using as the first and second derivative of the solution of problem (1). And this class methods generalizes of the known Multistep Second Derivative Methods with constant coefficients. Here is a complete comparison of methods using the first derivative of the solution of the problem (1). And have shown that the new class method of type (6) different class methods. By simple comparison get those methods like type objectivity, let us note that the advanced methods have some disadvantages. For example, to define the values yn+k-m by the advanced methods it is necessary that the values of the sought solutions at subsequent points must be known. Note that for solving this problem one can use the predictor-corrector method. By using the predictorcorrector method one can be expanded the region of stability for the stable advanced methods. Here described the application of the Multistep Methods to solve initial-value problem for Ordinary Differential Equations. However, this method can be applied with equal success to solve other problems. For example the initial-value problem for the Volterra Integral Differential Equations. To verify this it is enough to write the method (2) in the following from:
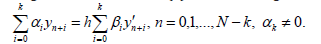
Acknowledgment
The authors thank Academician T. Aliyev, and Academician A. Abbasov for their useful Valuable advice. This work was partially supported by the Science Development Foundation under the President of the Republic of Azerbaijan - grant AEF-MCG-2022- 1(42)-12/4/1-M-4. Finally, the authors also thank the reviewers for their comments.
Conflict of Interest
The authors state express that there is no conflict of interest misunderstanding between them. We hereby confirm that all the methods in this manuscript are ours.
References
- Iserles A, Norset SP (1987) Two-step methods and bi-orthogonality. Math of Comput 180: 543-552.
- Dahlquist G (1956) Convergence and stability in the numerical integration of ordinary differential equations. Math Scand 4: 33-53.
- Hairer E, Lubuch C, Wanner G (2004) Geometric numerical integration, (2nd edn), Springer, p. 644.
- Mehdiyeva G, Ibrahimov V (2013) On the investigation of multistep methods with constant coefficients. Lap Lambert, Academi Publising, p. 314.
- Babushka I, Vitasek E, Prager M (1969) Numerical processes for solving differential equations. Mir, p. 368.
- Skvortsov L (2009) Explicit two-step runge-kutta methods. Math modeling 21: 54-65.
- Shura-Bura MR (1952) Error estimates for numerical integration of ordinary differential equations. Prikl matem and mech, № 5, pp. 575-588.
- Bakhvalov NS (1955) Some remarks on the question of numerical integration of differential equation by the finite-difference method, Academy of Science report, USSA, N3, pp. 805-808.
- Butcher J (1965) A modified multistep method for the numerical integration of ordinary differential equations. J Assoc Comput Math 12(1): 124-135.
- Ibrahimov VR (1984) Relationship between of the order and the degree for a stable forward-jumping formula, Prib. operator methods. urav Baku, Azerbaijan, pp. 55-63.
- Henrici P (1962) Discrete variable methods in ODG, John Wiley and Sons, Inc, New York. London.
- Ibrahimov VR (1990) A relationship between order and degree for a stable formula with advanced nodes. Computational Mathematics and Mathematical Physics (USSR) 30(4): 57-65.
- Ibrahimov V, Imanova M (2021) Multistep methods of the hybrid type and their application to solve the second kind Volterra integral equation. Symmetry 13(6): 1-23.
- Salma AA, Ahmedai AA, Sibanda P, Goqo SP, Rufai UO, et al. (2024) A block hybrid method with equally spaced grid points for third-order initial values problems. Applied math MDPI 4(1): 320-347.
- Adeyeye O, Omar Z (2016) New uniform order eight hybrid third derivative block method for solving second order initial value problems. Far East Journal of Mathematical Sciences (FJMS)© 2016 Pushpa Publishing House, Allahabad, India 100(9): 1515-1531.
- Mehdiyeva G, Ibrahimov V, Imanova M (2016) General theory of the applications of multistep methods to calculation of the energy of signals. In: Zeng QA (Ed.), wireless communications, networking and applications. Lecture Notes in Electrical Engineering, Springer, New Delhi, India 348: 1047-1056.
- Mehdiyeva G, Ibrahimov V, Imanova M (2012) Application of the hybrid method with constant coefficients to solving the integro-differential equations of first order. AIP Conference Proceedings 1493(1): 506-510.
- Akinfenwa OA, Akinnukawe B, Mudasiru SB (2015) A family of continuous third derivative block methods for solving stiff systems of first order ordinary differential equations. Journal of the Nigerian Mathematical Society 34(2): 160-168.
- Ibrahimov VR (2002) On the maximal degree of the k-step Obrechkoff’s method. Bulletin of Iranian Mathematical Society 28(1): 1-28.
- Imanova MN, Ibrahimov VR (2023) The new way to solve physical problems described by ODE of the second order with the special structure., WSEAS Transactions on Systems 22: 199-206.
- Muritala F, Azeez A, Jimoh K, Ogunniran M, Abdulmalik A, et al. (2023) K-Step block hybrid method for numerical approximation of fourth-order ordinary differential equations, Authorea.
- Omar Z, Alkasassbeh MF (2016) Generalized one -step third derivative implicit hybrid block method for the direct solution of second order ordinary differential equation, Applied Mathematical Sciences 10(9): 417-430.
- Mehdiyeva G, Ibrahimov V, Imanova M (2011) On a way for constructing numerical methods on the joint of multistep and hybrid methods. World Academy of Science, engineering and Technology 5(9): 240-243.
- Ibrahimov V, Imanova M (2023) On some modifications of the gauss quadrature method and its application to solve of the initial-value problem for ODE. Proceeding of 2022 International Conference on Wireless Communications, Networking and Applications (WCNA 2022), pp. 306-316.
- Kamoh NM, Aboiyar T, Kimbir A (2017) Continuous multistep methods for volterra integro-differential equational equations of the second order, Science World Journal 12(3): 1-14.
- Adewale James A, Adesanya O, Joshua S (2013) Continuous block method for the solution of second order initial value problems of ordinary differential equation. International Journal of Pure and Applied Mathematics 83(3): 405-416.
- Oghonyon JG, Solomon AO, Bishop SA (2015) A 5-step block predictor and 4-step corrector methods for solving general second order ordinary differential equations. Global Journal of Pure and Applied Mathematics 11(5): 3847-3862.
- Liu C, Hsu CW, Simos TE, Tsitouras Ch (2019) Phase fitted, six-step method for solving x” =f (t,x). Math Meth Appl Sci 42(11): 3942-3949.
- Samat F, Ismail ES (2020) A two-step modified explicit hybrid method with step-size dependent parameter for oscillatory problems. Journal of Mathematics, pp. 1-7.
- Liu C, Hsu CW, Tsitouras CH, Simos TE (2019) Hybrid Numerov type methods with coefficients trained to perform better on classical orbits. Bulletin of the Malaysian Mathematical Sciences Society 42(24): 2119-2134.
- Yahaya YA, Sagir AM, Tech M (2013) An order five implicit 3-step block method for solving ordinary differential equations, The Pacific Journal of Science and Technology 14(1): 176-183.
- Mehdiyeva G Yu, Ibrahimov VR, Imanova MN (2012) Application of a second derivative multi-step method to numerical solution of Volterra integral equation of second kind. Pakistan Journal of Statistics and Operation Research 8(2): 245-258.
- Mehdiyeva G Yu, Ibrahimov V, Imanova M (2023) An application of the hybrid methods to the numerical solution of ordinary diffrential equations of second order, Kazakh National University named after Al-Farabi. Journal of treasury series, mathematics, mechanics, computer science, Almaty, tom 75(4): 46-54.
- Mehdiyeva GY, Imanova MN, Ibrahimov VR (2013) The application of the hybrid method to solving the Volterra integro-differential equation. Proceedings of the World Congress on Engineering 3-5: 186-190.
- Simos TE (2012) Optimzing a hybrid two-step method numerical solution of the Schrodinger equation and related problems with respect to phase-lag, Journal of Applied Mathematics, p. 17
- Sani AY (2013) Derivation and application of six-point linear multistep numerical method for solution of second order initial value problems. IOSR Journal of Mathematics (IOSR-JM) 7(2): 23-29.
- Ajani M, Shokri A, Ezekiel O (2023) A one point third derivative hybrid multistep technique for solving second order oscillatory and periodic problems. Hindawi Journal of Mathematics, p. 12.
- Nathaniel K, Geoffrey K, Joshua S (2021) Continuous one step linear multi-step hybrid block method for the solution of first order linear and nonlinear initial value problem of ordinary differential equations. Recent Developments in the Solution of Nonlinear Differential Equations, p. 1-9
- Kamoh NM, Aboiyar T, Kimbir AR (2017) Continuous multistep methods for Volterra Integro-differential equational equations of the second order, Science World Journal 12(3): 1-14.
- Mehdiyeva G, Imanova M, Ibrahimov V (2016) An application of mathematical methods for solving of scientific problems, British Journal of Applied Science & Technology 14(2): 1-14.
- Mehdiyeva G, Ibrahimov V, Imanova M (2016) Some refinement of the notion of symmetry for the Volterra integral equations and the construction of symmetrical methods to solve them. Journal of Computational and Applied Mathematics 306: 1-9.
- Juraev DA, Noeiaghdam S (2021) Regularization of the Ill-posed Cauchy problem for matrix factorizations of the Helmholtz equation on the plane. Axioms, 10(2): 1-14.
- Juraev DA (2021) Solution of the ill-posed Cauchy problem for matrix factorizations of the Helmholtz equation on the plane. Global and Stochastic Analysis 8(3): 1-17.
- Juraev DA (2022) On the solution of the Cauchy problem for matrix factorizations of the Helmholtz equation in a multidimensional spatial domain. Global and Stochastic Analysis 9(2): 1-17.
- Juraev JA, Shokri A, Marian D (2022) Regularized solution of the Cauchy problem in an unbounded domain. Symmetry 14(8): 1-13.
- Zhuraev DA (2018) cauchy problem for matrix factorizations of the Helmholtz equation. Ukrainian Mathematical Journal 69: 1583-1592.
- Juraev DA, Elsayed EE, Bulnes JJD, Agarwal P, Saeed RK (2023) History of ill-posed problems and their application to solve various mathematical problems. Engineering Applications 2(3): 279-290.
- Bulnes JD, Juraev DA, Bonilla JL, Travassos MAI (2023) Exact decoupling of a coupled system of two stationary Schrödinger equations. Stochastic Modelling & Computational Sciences 3(1): 23-28.
- Juraev DA (2023) The Cauchy problem for matrix factorization of the Helmholtz equation in a multidimensional unbounded domain. Bulletin of the Paranaense Mathematical Society 41: 1-18.
© 2024 Vagif Ibrahimov. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






