Quantum Matrices Using Quantum Gates

Introduction

In physics, the size of iotas (atoms) and electrons demonstrates that how things move at every day at different sizes and speeds. In classical mechanics, objects exist in a definite place at a definite time. However, in quantum mechanics, objects rather exist in a haze of probability; they have a specific possibility of being at point A, another chance of being at point B. Certain properties like position, speed and colour can sometimes occur in exact, set amounts, like a dial that “clicks” from number to number. This challenged a fundamental assumption of classical mechanics, which said that such properties should exist on an even, continuous spectrum. To illustrate the possibility that a few properties “clicked” like a dial with definite settings, experts coined the word “quantized” [1].

Beam Splitter

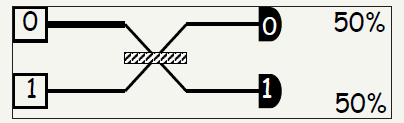
An example was demonstrated by Prof. Marek Perkowski from Portland State University using beam splitter and based on that how quantum circuits could work. “Half of the photons leaving the light source arrive at detector A; the other half arrive at detector B” [2,3] (Figure 1 & 2).

figure 1: Demonstrates the light beam splitting to two directions [3].

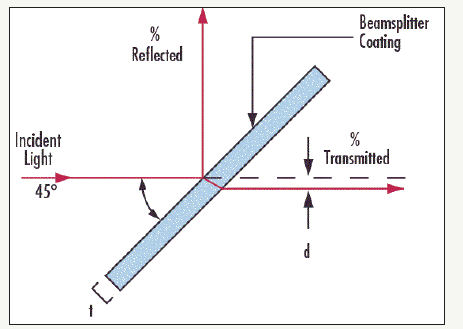
figure 2: Demonstrates simplest circuit of light beam splitter in Quantum Circuit [1].

Linear Algebra in Quantum Mechanics

The most convenient way to understand linear operators is in terms of their matrix representations. In fact, the linear operator and matrix viewpoints turn out to be entirely equivalent. For more information on linear operator representation can refer Reference No 7

Vectors can be written as:

For readability format it can be written as (1,2) and for two level quantum systems used as qubits, we can identify the state |0” with the vector (1, 0), and similarly |1” with (0, 1) [4-6].

Square Matrices using Quantum Gates

A simulation was performed on Hadamard Gates to generate square matrices considering entanglements of quantum bits [7].

A. Square matrix using hadamard gate using two quantum circuits (Figure 3) (Table 1)

Table 1: Measured output results of two quantum circuits.

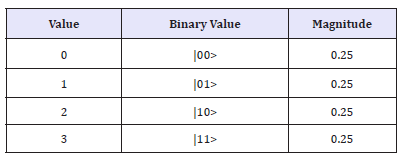
figure 3: Demonstrates Square Matrix using two quantum circuits and total usage of 4 quantum bits.

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |00>

Val: +0.50000+0.00000i

mag2: 25.0000%, phase: 0.00o

Amplitude of |01>

Val: 0.50000+0.00000i

mag2: 25.0000%, phase: 0.00o

Amplitude of |10>

Val: +0.50000+0.00000i

mag2: 25.0000%, phase: 0.00o

Amplitude of |01>

Val: 0.50000+0.00000i

mag2: 25.0000%, phase: 0.00o

B. Square matrix using hadamard gate using four quantum circuits (Figures 4-6) (Table 2)

Table 2: Measured output results of four quantum circuits.

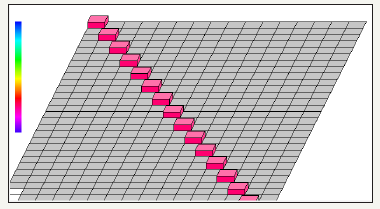
figure 4: Demonstrates the graph of two quantum circuits square Matrix in QCAD (Quantum Computer Aided Design) [5,6].

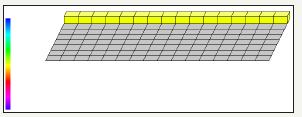
figure 5: Demonstrates Square Matrix using four quantum circuits and total usage of 16 quantum bits.

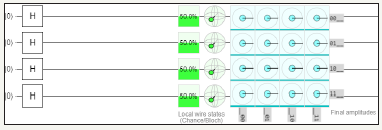
figure 6: Demonstrates the graph of four quantum circuits square Matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

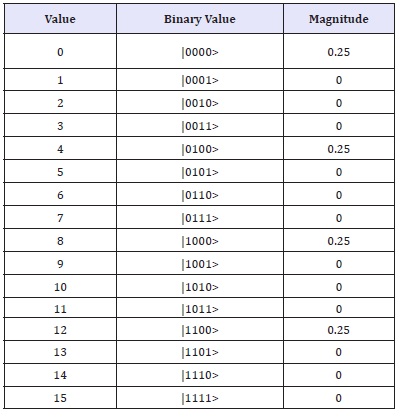
Amplitude of |0000>

Val: +0.25000+0.00000i>

mag2: 6.25%, phase: 0.00o

C. Square matrix using hadamard gate using six quantum circuits (Figures 7 & 8) (Table 3)

Table 3: Measured output results of six quantum circuits.

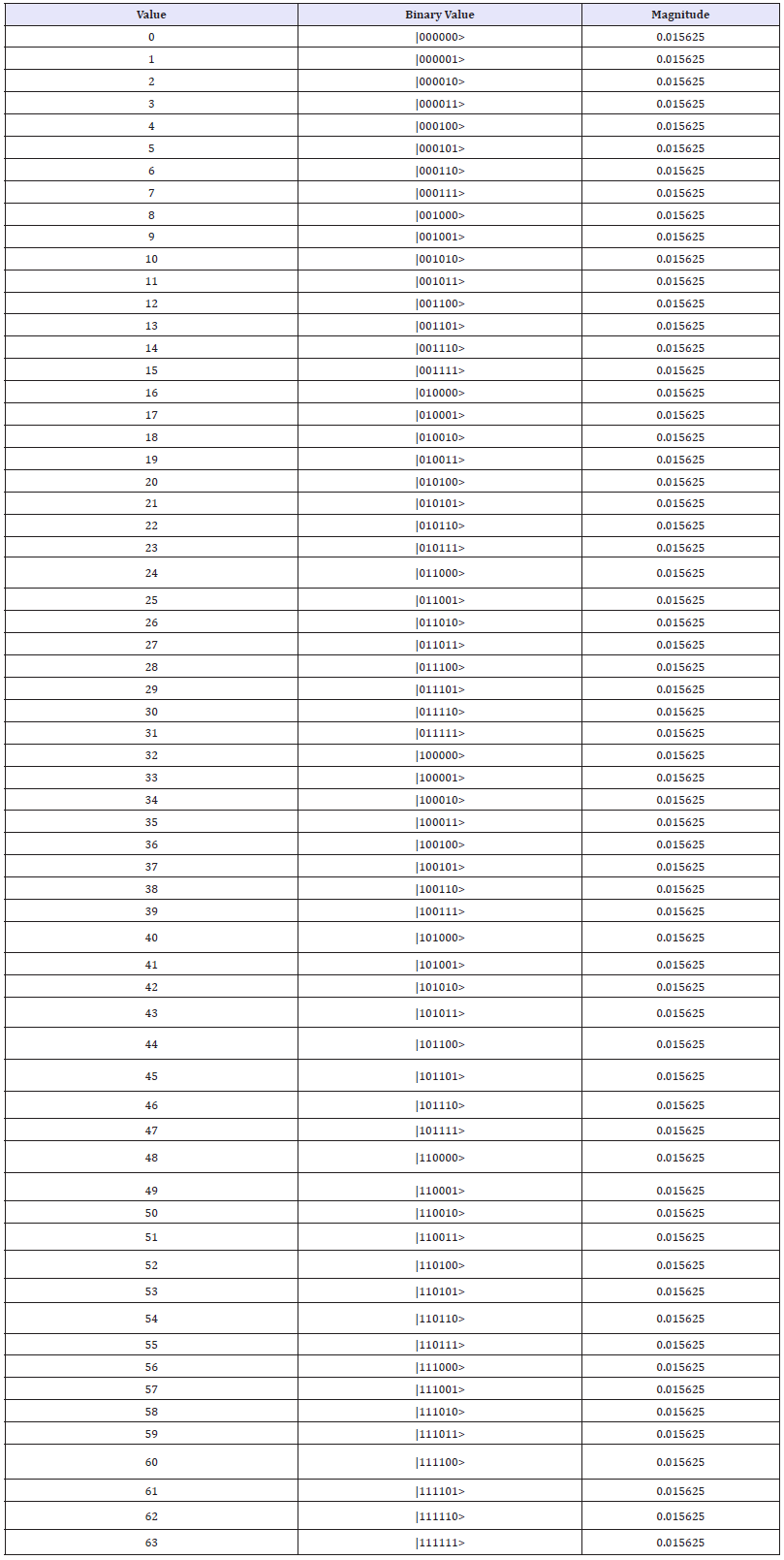
figure 7: Demonstrates Square Matrix using six quantum circuits and total usage of 64 quantum bits.

figure 8: Demonstrates the graph of six quantum circuits square Matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |000000>

Val: +0.12500+0.00000i

mag2: 1.5625%, phase: 0.00o

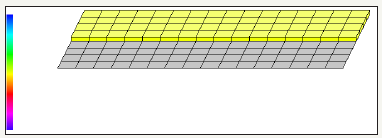
D. Square matrix using hadamard gate using eight quantum circuits (Figures 9 & 10)

figure 9: Demonstrates Square Matrix using eight quantum circuits and total usage of 256 quantum bits.

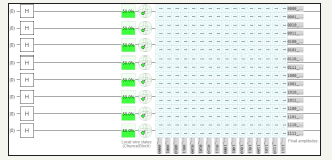
figure 10: Demonstrates the graph of eight quantum circuits square Matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |00000000>

Val: +0.06250+0.00000i

mag2: 0.3906%, phase: 0.00o

E. Square matrix using hadamard gate using ten quantum circuits (Figures 11 & 12)

figure 11: Demonstrates Square Matrix using ten quantum circuits and total usage of 1024 quantum bits.

figure 12: Demonstrates the graph of ten quantum circuits square Matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |0000000000>

Val: +0.03125+0.00000i

mag2: 0.0977%, phase: 0.00o

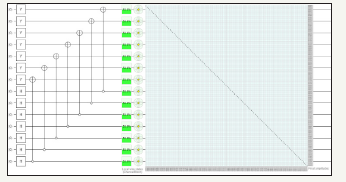
F. Square matrix using hadamard gate using twelve quantum circuits (Figure 13)

figure 13: Demonstrates Square Matrix using twelve quantum circuits and total usage of 4096 quantum bits

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |000000000000>

Val: +0.01562+0.00000i

mag2: 0.0244%, phase: 0.00o

G. Square matrix using hadamard gate using fourteen quantum circuits (Figure 14)

figure 14: Demonstrates Square Matrix using fourteen quantum circuits and total usage of 16384 quantum bits.

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |00000000000000>

Val: +0.00781+0.00000i

mag2: 0.0061%, phase: 0.00o

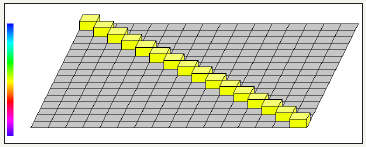
H. Square Matrix using hadamard gate using sixteen quantum circuits (Figure 15)

figure 15: Demonstrates Square Matrix using sixteen (max) quantum circuits and total usage of 65536 quantum bits.

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +1.0000, φ+0.00o, θ: +90o

x: +1.0000, y: 0.0000, z: +0.0000

Amplitude of |0000000000000000>

Val: + 0.00391+0.00000i

mag2: 0.0014%, phase: 0.00o

Observations from square matrix

1. Successfully performed square matrix utilizing sixteen (max) quantum circuits considering entanglement process using only Hadamard gate

2. Real value of each quantum bit is equal for all quantum bits and for every addition of two quantum circuit there is a decrease of real value by half

3. Magnitude of each quantum bit decreases by half for every addition of quantum circuit (In this case one fourth because addition of two circuits)

4. Study of Hadamard gate has been performed

5. Graphs of twelve, fourteen and sixteen quantum circuits are not used due to complexity of the circuit and limitation of the tool to process large quantum circuits

6. Tables of eight, ten, twelve, fourteen and sixteen quantum circuits are avoided due to results are similar as previous data except for magnitudes.

Identity Matrices using Quantum Gates

A simulation was performed on various gates of Hadamard, Pauli Y Gates and NOT gates to generate identity matrices considering entanglements

A. Identity matrix using hadamard, Pauli Y and NOT gate using two quantum circuits (Figure 16 & 17) (Table 4)

Table 4: Measured output results of two quantum circuits.

figure 16: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing two quantum circuits and total usage of 2 quantum bits.

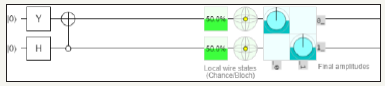
figure 17: Demonstrates the graph of two quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90o

x: +0.0000, y: 0.0000, z: +0.0000

Amplitude of |00>

Val: +0.00000+0.70711i

mag2: 50.0000%, phase: +90.00o

Amplitude of |01>

Val: +0.00000+0.00000i

mag2: 00.0000%, phase: +0.00o

Amplitude of |10>

Val: +0.00000+0.70711i

mag2: 50.0000%, phase: +90.00o

Amplitude of |11>

Val: +0.00000+0.00000i

mag2: 00.0000%, phase: +0.00o

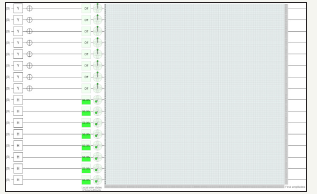
B. Identity matrix using hadamard, Pauli Y and NOT gate using four quantum circuits (Figure 18-20) (Table 5)

Table 5: Measured output results of four quantum circuits.

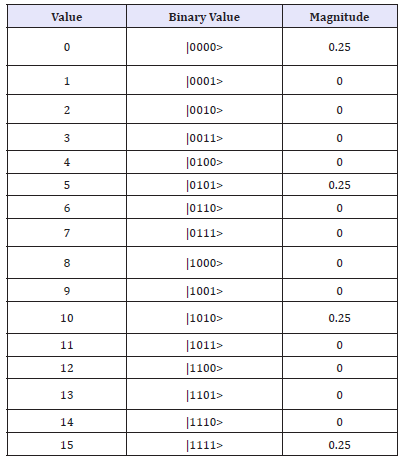
figure 18: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing four quantum circuits and total usage of 4 quantum bits.

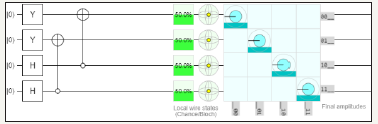
figure 19: Demonstrates four quantum circuit Identity Matrix using QCAD.

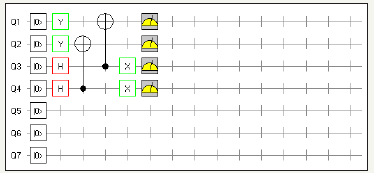
figure 20: Demonstrates the graph of four quantum circuits identity matrix in QCAD (Quantum Computer Aided Design)

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90o

x: +0.0000, y: 0.0000, z: +0.0000

Amplitude of |0000>

Val: -0.50000+0.00000i

mag2: 25.0000%, phase: +180.00o

Amplitude of |0001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

C. Identity matrix using hadamard, Pauli Y and NOT gate using six quantum circuits (Figure 21-23) (Table 6)

Table 6: Measured output results of six quantum circuits.

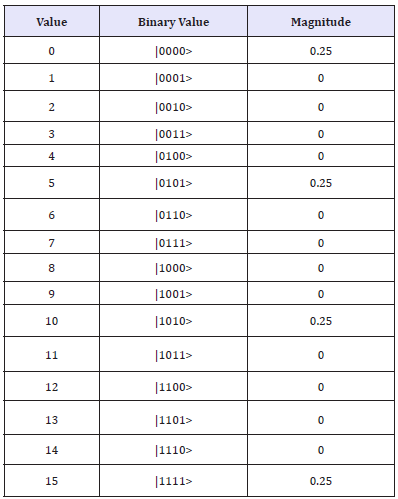
figure 21: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing six quantum circuits and total usage of 8 quantum bits.

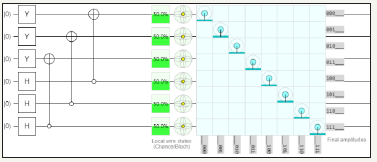
figure 22: Demonstrates six quantum circuit Identity Matrix using QCAD.

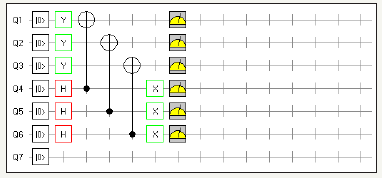
figure 23: Demonstrates the graph of six quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

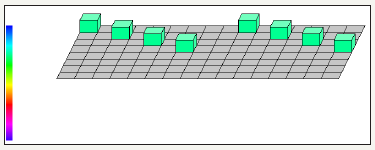
Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |000000>

Val: +0.00000+0.35355i

mag2: 12.5000%, phase: -90.00o

Amplitude of |000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

D. Identity matrix using hadamard, Pauli Y and NOT gate using eight quantum circuits (Figure 24-26)

figure 24: Demonstrates the graph of six quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

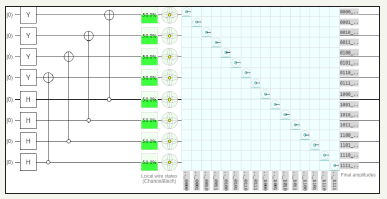
figure 25: Demonstrates the graph of six quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

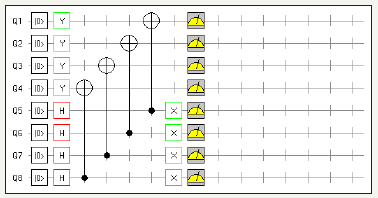
figure 26: Demonstrates the graph of six quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |00000000>

Val: +0.25000+0.00000i

mag2: 6.2500%, phase: +00.00o

Amplitude of |00000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

E. Identity matrix using hadamard, Pauli Y and NOT gate using ten quantum circuits (Figure 27-29)

figure 27: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing ten quantum circuits and total usage of 32 quantum bits

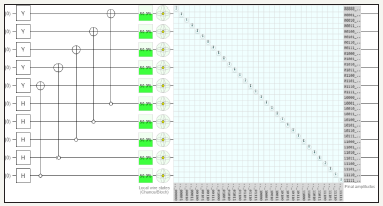
figure 28: Demonstrates ten quantum circuit Identity Matrix using QCAD

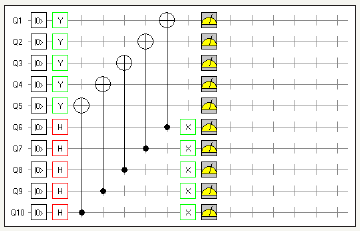
figure 29: Demonstrates the graph of ten quantum circuits identity matrix in QCAD (Quantum Computer Aided Design).

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |0000000000>

Val: +0.00000+0.17678i

mag2: 3.1250%, phase: +90.00o

Amplitude of |0000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

F. Identity matrix using hadamard, Pauli Y and NOT gate using twelve quantum circuits (Figure 30)

figure 30: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing twelve quantum circuits and total usage of 64 quantum bits

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |000000000000>

Val: -0.12500+0.0000i

mag2: 1.5625%, phase: +180.00o

Amplitude of |000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

figure 31: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing fourteen quantum circuits and total usage of 128 quantum bits.

G. Identity matrix using hadamard, Pauli Y and NOT gate using fourteen quantum circuits (Figure 31)

Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ+0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |00000000000000>

Val: +0.12500+0.08839i

mag2: 0.7812%, phase: -90.00o

Amplitude of |00000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

H. Identity matrix using hadamard, Pauli Y and NOT gate using sixteen (max) quantum circuits (Figure 32)

figure 32: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing sixteen (max) quantum circuits and total usage of 256 quantum bits

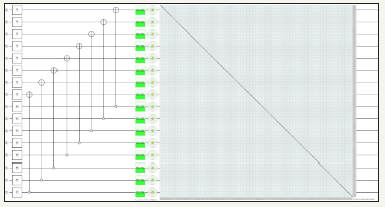
Notes:

Chance of being ON if measured: 50.00000%

Bloch sphere representation of local state

r: +0.0000, φ +0.00o, θ: +90.00o

x: +0.0000, y: +0.0000, z: +0.0000

Amplitude of |0000000000000000>

Val: +0.06250+0.00000i

mag2: 0.3906%, phase: +00.00o

Amplitude of |0000000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

Observations from identity matrix

1. Successfully performed identity matrix utilizing sixteen (max) quantum circuits considering entanglement process using Hadamard, Pauli X and NOT gates

2. Real and complex values of each quantum bit is equal for all quantum bits

3. Real values decrease by half for addition of fourth, eighth, twelve and sixteenth quantum circuit

4. Complex value decreases by half for addition of second, sixth, tenth and fourteenth quantum circuit

5. Magnitude of each quantum bit decreases by half for every addition of two quantum circuit

6. Graphs of twelve, fourteen and sixteen quantum circuits are not used due to complexity of the circuit and limitation of the tool to process large quantum circuits

7. Tables of eight, ten, twelve, fourteen and sixteen quantum circuits are avoided due to results are similar as previous data except for magnitudes.

Transposing of Matrices using quantum Gates

A simulation was performed for transposition of Matrix

A. Transposition of matrix using hadamard, Pauli Y, NOT, and swap gate using two quantum circuits (Figure 33)

figure 33: Demonstrates Identity Matrix using Pauli Y, Hadamard Gate and NOT gate utilizing sixteen (max) quantum circuits and total usage of 256 quantum bits

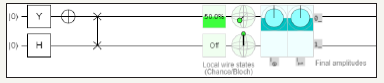
Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ : +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for second quantum circuit

r: +1.0000, +0.00o, : +90.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |00>

Val: +0.00000+0.70711i

mag2: 50.0000%, phase: +90.00o

Amplitude of |10>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

(Figure 34) (Table 7) (Figure 35)

Table 7: Measured output results of two quantum circuits.

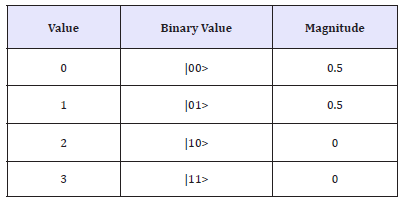
figure 34: Demonstrates the graph of two quantum circuits before transposition of matrix in QCAD (Quantum Computer Aided Design)

figure 35: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing two quantum circuits and total usage of 2 quantum bits.

Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for second quantum circuit

r: +1.0000, +0.00o, : +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |00>

Val: +0.00000+0.70711i

mag2: 50.0000%, phase: +90.00o

Amplitude of |01>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 36) (Table 8)

Table 8: Measured output results of two quantum circuits.

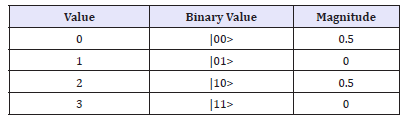
figure 36: Demonstrates the graph of two quantum circuits after transposition of matrix in QCAD (Quantum Computer Aided Design).

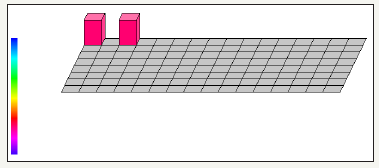
B. Transposition of Matrix using Hadamard, Pauli Y, NOT, and swap gate using four quantum circuits (Figure 37)

figure 37: Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing four quantum circuits and total usage of 4 quantum bits.

Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for third quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |0000>

Val: +0.50000+0.00000i

mag2: 25.0000%, phase: +180.00o

Amplitude of |0100>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 38) (Table 9) (Figure 39)

Table 9: Measured output results of four quantum circuits.

figure 38: Demonstrates the graph of four quantum circuits before transposition of matrix in QCAD (Quantum Computer Aided Design)

figure 39: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing four quantum circuits and total usage of 4 quantum bits

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for third quantum circuit

r: +1.0000, φ +0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |0000>

Val: +0.50000+0.00000i

mag2: 25.0000%, phase: +180.00o

Amplitude of |0001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 40) (Table 10)

figure 40: Demonstrates the graph of four quantum circuits after transposition of matrix in QCAD (Quantum Computer Aided Design)

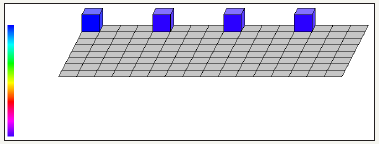
Table 10: Measured output results of four quantum circuits.

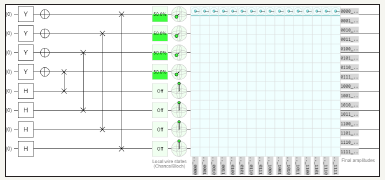
C. Transposition of Matrix using Hadamard, Pauli Y, NOT, and swap gate using six quantum circuits (Figure 41)

figure 41: Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing six quantum circuits and total usage of 8 quantum bits

Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for fourth quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |000000>

Val: +0.00000-0.35355i

mag2: 12.5000%, phase: -90.00o

Amplitude of |001000>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 42) (Table 11) (Figure 43)

Table 11: Measured output results of six quantum circuits.

figure 42: Demonstrates the graph of six quantum circuits before transposition of matrix in QCAD (Quantum Computer Aided Design)

figure 43: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing six quantum circuits and total usage of 8 quantum bits

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for fourth quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |000000>

Val: +0.00000-0.35355i

mag2: 25.0000%, phase: +180.00o

Amplitude of |000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 44) (Table 12)

Table 12: Measured output results of six quantum circuits

figure 44: Demonstrates the graph of six quantum circuits after transposition of matrix in QCAD (Quantum Computer Aided Design)

D. Transposition of matrix using hadamard, Pauli Y, NOT, and swap gate using eight quantum circuits (Figure 45)

figure 45: Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing eight quantum circuits and total usage of 16 quantum bits

Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for fifth quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |00000000>

Val: +0.25000-0.00000i

mag2: 6.2500%, phase: +0.00o

Amplitude of |00010000>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 46 & 47)

figure 46: Demonstrates the graph of eight quantum circuits before transposition of matrix in QCAD (Quantum Computer Aided Design).

figure 47: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing eight quantum circuits and total usage of 16 quantum bits.

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for fifth quantum circuit

r: +1.0000, φ +0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |00000000>

Val: +0.25000+0.00000i

mag2: 6.2500%, phase: +0.00o

Amplitude of |00000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figure 48)

figure 48: Demonstrates the graph of eight quantum circuits after transposition of matrix in QCAD (Quantum Computer Aided Design).

figure 49: Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing ten quantum circuits and total usage of 32 quantum bits.

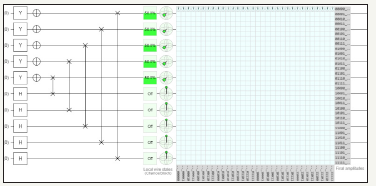
Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for sixth quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |0000000000>

Val: +0.00000-0.17678i

mag2: 3.1250%, phase: +90.00o

Amplitude of |0010100000>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o (Figures 50 & 51)

figure 50: Demonstrates the graph of ten quantum circuits before transposition of matrix in QCAD (Quantum Computer Aided Design).

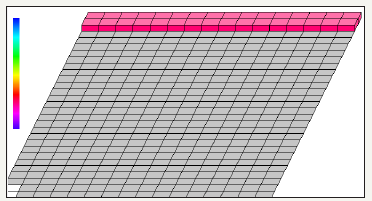
figure 51: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing ten quantum circuits and total usage of 32 quantum bits.

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for sixth quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |0000000000>

Val: +0.00000+0.17678i

mag2: 3.1250%, phase: +90.00o

Amplitude of |0000000001>

Val: +0.00000+0.00000i

mag²: 0.0000%, phase: +0.00o (Figure 52)

figure 52: Demonstrates the graph of ten quantum circuits after transposition of matrix in QCAD (Quantum Computer Aided Design).

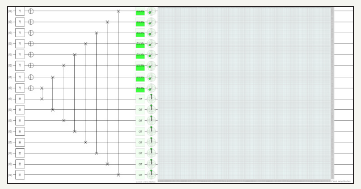
F. Transposition of matrix using hadamard, Pauli Y, NOT, and swap gate using twelve quantum circuits (Figure 53)

figure 53: Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing twelve quantum circuits and total usage of 64 quantum bits.

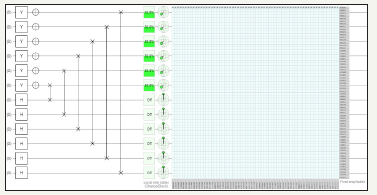
Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for seventh quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |000000000000>

Val: -0.12500-0.00000i

mag²: 1.5625%, phase: +180.00o

Amplitude of |000001000000>

Val: +0.00000+0.00000i

mag²: 0.0000%, phase: +0.00o (Figure 54)

figure 54: Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing twelve quantum circuits and total usage of 64 quantum bits.

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for seventh quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |000000000000>

Val: -0.12500+0.00000i

mag2: 1.5625%, phase: +180.00o

Amplitude of |000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

G. Transposition of matrix using hadamard, Pauli Y, NOT, and swap gate using fourteen quantum circuits (Figure 55)

figure 55:Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing fourteen quantum circuits and total usage of 128 quantum bits.

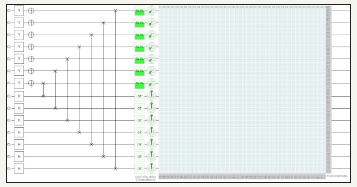
Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for eighth quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x

: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |00000000000000>

val: +0.00000-0.08839i

mag2: 1.5625%, phase: +180.00o

Amplitude of |00000010000000>

Val: +0.00000+0.0000i

mag2: 0.0000%, phase: +0.00o (Figure 56)

figure 56:Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing fourteen quantum circuits and total usage of 128 quantum bits.

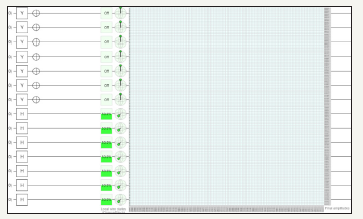
Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ+0.00o, θ: +0.00o

x: +1.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for eighth quantum circuit

r: +1.0000, φ +0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |00000000000000>

Val: +0.00000-0.08839i

mag2: 0.7812%, phase: -90.00o

Amplitude of |00000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

H. Transposition of matrix using hadamard, Pauli Y, NOT, and swap gate using sixteen quantum circuits (Figure 57)

figure 57:Demonstrates before transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing sixteen quantum circuits and total usage of 256 quantum bits.

Notes:

Chance of being ON for Y Pauli Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Bloch sphere representation of local state for ninth quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Amplitude of |0000000000000000>

Val: +0.06250-0.00000i

mag2: 0.3906%, phase: +0.00o

Amplitude of |0000000100000000>

Val: +0.00000+0.0000i

figure 58:Demonstrates after transposition of Matrix using Pauli Y, Hadamard, NOT and swap gates utilizing sixteen quantum circuits and total usage of 256 quantum bits

mag2: 0.0000%, phase: +0.00o (Figure 58)

Notes:

Chance of being ON for Hadamard Gate if measured: 50.00000%

Bloch sphere representation of local state for first quantum circuit

r: +1.0000, φ +0.00o, θ: +0.00o

x: +0.0000, y: +0.0000, z: +1.0000

Bloch sphere representation of local state for ninth quantum circuit

r: +1.0000, φ+0.00o, θ: +90.00o

x: +1.0000, y: +0.0000, z: +0.0000

Amplitude of |0000000000000000>

Val: +0.06250+0.00000i

mag2: 0.3906%, phase: +0.00o

Amplitude of |0000000000000001>

Val: +0.00000+0.00000i

mag2: 0.0000%, phase: +0.00o

Observations from transposition of matrix

1. Successfully performed transposition of matrix utilizing sixteen (max) quantum circuits considering entanglement process using Hadamard, Pauli X and NOT gates

2. Magnitude and phase don’t change in transposition of Matrix

3. Magnitude of each quantum bit decreases by half for every addition of two quantum circuit

4. Graphs of twelve, fourteen and sixteen quantum circuits are not used due to complexity of the circuit and limitation of the tool to process large quantum circuits

5. Tables of eight, ten, twelve, fourteen and sixteen quantum circuits are avoided due to limitation of the tool to process large quantum circuits.

Applications of Quantum Matrices

1. Quantum Matrices can be used to solve system performance with a big RAM and/or a high clock rate for Quantum Central Processing Unit (QCPU)

2. Studying Quantum Matrices and their properties is of crucial importance in trying to improve linear solvers efficiency in Quantum Processor/Quantum computer

3. If constructing a larger system in a quantum processor with the same pattern (2 on the diagonal, -1 on the upper and lower diagonal) and put a right-hand side with only positive entries, we can still claim that the solution exists and it’s positive and the number of operations needed to solve it, where n is the size of the system [7].

Results

What claimed are

1. Successfully processed 65536 quantum bits of information for 16 quantum circuits to achieve square matrix considering whole process in entanglement

2. Square matrix for quantum bits is generated with respect to phase, angle, complex values and magnitude of the results

3. Successfully processed 256 quantum bits of information for identity matrix and transposition of matrix with respect to phase, angle, real, complex values and magnitude.

4. Identity matrix for quantum bits is generated with respect to phase, angle, complex values and magnitude of the results.

5. Transposition of matrix for quantum bits is generated with respect to phase, angle, complex values and magnitude of the results.

6. Study of Hadamard Gates are performed and observations are noted.

7. Study of various phases, angles, complex values, magnitudes and amplitudes of the quantum bits are performed and is documented in this paper

8. Based on results and above data other matrices such as row matrix, column matrix, rectangular matrix, diagonal matrix, scalar matrix, triangular matrix, null matrix can be constructed using quantum bits.

Conclusion

Based on the results Quantum Matrices can be constructed and processed 65536 quantum bits have been processed. And any quantum matrices can be constructed using this method which will help in performance of the Quantum Computers.

Novelty

Novelty in this paper are:

Constructed square Matrix using quantum bits

Constructed Identity Matrix using quantum bits

Performed Transposition of Matrix using quantum bits

Processed 65536 (max) quantum bits of information for 16

quantum circuits considering whole process in entanglement for square matrix

Processed 256 quantum bits of information for 16 quantum circuits considering whole process in entanglement for identity matrix

Processed 256 quantum bits of information for 16 quantum circuits considering whole process in entanglement for transposition of matrix.

Nomenclature

r: position

: represents wavefuntion to solve from the Schrödinger equation (varies with situation and number of quantum bits)

: Angle in degrees

i: the imaginary unit

x: x component

y: y component

z: z component

Val: Value

mag²: magnitude in square

Acknowledgment

Author would like to thank Prof. Navarun Gupta, Prof. Hassan Bajwa, Prof. Linfeng Zhang and Prof. Hmurcik for their academic support. Author also thanks anonymous reviewers for their comments.

References

1. Coolman R (2014) What Is Quantum Mechanics? Live Science.
2. Perkows M (2002) Introductory Lecture on Quantum Computing.
3. Edmund Optics What are Beam splitters? | Edmund Optics, Barrington, USA.
4. Quirk Quirk: Quantum Circuit Simulator.
5. QCAD QCAD - CAD for Quantum Computer Simulator.
6. Bartgol What is the usefulness of matrices?
7. Nielsen MA, Chuang IL (2016) Quantum computation and quantum information. Cambridge University Press, Cambridge, UK.