- Submissions

Full Text
Research in Medical & Engineering Sciences
Speed of Light and Gravity, 𝒈 = 𝑮𝒄𝟐/𝒓
Greg Poole*
Industrial Tests, USA
*Corresponding author: Greg Poole, Industrial Tests, Inc Rocklin, CA USA
Submission: November 04, 2019; Published: November 13, 2019

ISSN: 2576-8816Volume8 Issue3
Abstract
The speed of light and the lunar light year of the Earth have been used to calculate a centripetal acceleration. The results align exactly with gravity at the surface of the Earth or 9.8m/s2. It is thought that the electromagnetic field of the Earth extends in a circular path to the far edges of the solar system and the speed of light contributes to the centripetal acceleration experienced on Earth. The author concludes that electromagnetism is the driving force of gravity in the near- and far-fields of the solar system.
Keywords: Centripetal acceleration; Gravity; Light year; Lunar calendar; Synodic
Introduction
The first known lunar calendar was found at Warren Field in Scotland and has been dated to c. 8000 BCE, during the Mesolithic period [1]. In ancient Egypt a lunar calendar was used for religious and agricultural purposes. Present-day lunisolar calendars include the Chinese, Hindu, and Thai calendars. Synodic months are 29 or 30 days in length, making a lunar year of 12 months about 11 days shorter than a solar year. Some lunar calendars do not use intercalation, such as most Islamic calendars. The Hebrew calendar uses the most common form of intercalation which is to add an additional month every second or third year. In 1699, Sir Isaac Newton proposed a new calendar based on lunar months [2]. Since each lunation is approximately 29 1⁄2 days (29 days, 12 hours, 44 minutes, 3 seconds, or 29.530588 days), it is common for the months of a lunar calendar to alternate between 29 and 30 days. Since the period of twelve such lunations, a lunar year, is only 354 days, 8 hours, 48 minutes, 34 seconds.
Calculating the earth’s lunar light year
A light-year is defined as the distance that light can travel in 1 year. Typically, we calculate this by multiplying he speed of light by 1 year (or 3.1557 x 107 seconds) to find the distance:
𝑑 = 𝑐 × 𝑡
𝑑 = 3 × 108 𝑚/𝑠 × 3.1557 × 107𝑠
𝑑 = 9.4605 × 1015 𝑚𝑒𝑡𝑒𝑟𝑠
However, the Lunar calendar or synodic period of the moon is based on 354 days in a year. Using this ancient method of the calendar year results in 1 year being equal to 2.8133 × 107 seconds. Inserting this value into our equation and I obtain the following
𝑑 = 9.18 × 1015 meters
Calculating centripetal acceleration (m/s2) of the speed of light
The centripetal ('center-seeking') acceleration is the motion inwards, towards the center of a circle. The acceleration is equal to the square of the velocity, divided by the radius of the circular path. The maximum theoretical velocity of an object circling the globe is the speed of light.

where,
a=acceleration(inward)
v=c, or 3 × 108m/s
r= radius of a lunar light year, 9.18 × 1015 meters
When we insert these values in the centripetal acceleration equation, we obtain a result of 9.809 m/s2, which represents gravity at the surface of the Earth. The margin of error is less than 1%. In its final form Newtons Gravitational Constant is added to keep the equation proportional in the near and far field.
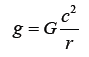
Conclusion
My calculations have shown that at the extreme edge of the electromagnetic field enveloping Earth the velocity of the smallest particles of light, photons, are speeding around the Earth and contributing to Earth’s centripetal acceleration. This is the furthest part of the electromagnetic field which is relatively “weak” compared to the near field. According to one author with expertise in general relativity, “For weak fields, though, one can describe the general relativity theory in a sort of Newtonian language” [3]. In general relativity, in the case of weak fields, the effect of propagation delay is almost exactly cancelled out, and general relativity very nearly produces a Newtonian result. The cancellation of propagation delay is almost exact for constant velocity. This relativist also states that electromagnetism calculations in a weak field produce identical results as general relativity calculations. Based on my equation, I would go a step further and say they are identical radiation patterns because it is the same light source of radiation. And, that for the “far field” where the electromagnetic field is very weak and the velocity of light is constant, it is not “a sort of” Newtonian equation- it is a Newtonian equation.
In electrodynamic theory, a charge moving at constant speed does not radiate. In our case the charge is the photon, which is a very weak charge to begin with. By the time it reaches the far field it is even weaker still. However, I point out that field intensity is not a part of this new equation, it is strictly limited to the speed of the photon that creates a centripetal acceleration. In terms of radiating or not radiating; using my equation for the weak far-field I intuit radiation intensity so weak; it becomes nearly immaterial to its velocity and inward acceleration. Radiation strength is superfluous for solving g = c2/ r.
This discussion supporting Newtonian representation of the far-field, is however, limited to the far-field. The near field, which includes the inverse square law, 1/r2 and a propagation delay, is rooted in general relativity. This is a separate equation that I have recently derived which includes a time constant, or propagation delay. The near-field will be a much-involved discussion and will be covered in a separate paper. According to antenna theory, there is also a third quasi-electrostatic field very near the radiation source, which incorporates a 1/𝑟3 term, which is even more complex and will be presented in a third paper.
There is a 3:1 relationship between gravity and electromagnetic antenna theory that includes the spherical components of 1/𝑟, 1/𝑟2 and 1/𝑟3. General relativity will add to the complexity of marrying the electromagnetic field to gravity Douglas M. Snyder, in his published article, which can be accessed on the CERN server, “A Connection between Gravitation and Electromagnetism” states, that “It has been extremely difficult to integrate gravitation with the other fundamental forces of nature. It is clear, though, that gravitation depends on a fundamental characteristic of light in the special theory, namely the finite and invariant velocity of light. It is the case that this finite and invariant velocity of light holds only in local Lorentz frames, unless of course one is concerned with flat spacetime. But in principle, the velocity of light is finite and invariant locally, even if on a global level in the general theory it cannot be said to generally have an invariant velocity [4]. Based on the results of this paper, I conclude that in the “far-field”, gravity is a centripetal acceleration derived from the speed of light [5]. The result of this paper is the foundational equation for my new Theory of Electro Relativity [6]. Based on the results of this paper, I conclude that in the “far-field”, gravity is a centripetal acceleration derived from the speed of light [5]. The result of this paper is the foundational equation for my new Theory of Electro Relativity [6].
Acknowledgements
The author wishes to acknowledge Jesus Christ for lighting the world. The truth shall make you free.
References
- Nancy O (2013) Scotland lunar-calendar find sparks stone age rethink. Phys Org, USA.
- Ari B, Eduardo VE (2010) Reform of the julian calendar as envisioned by Isaac newton. Notes and Records of the Royal Society of London 59( 3): 223-254.
- Steve C, Matthew W, Geoffrey L (2011) Does gravity travel at the speed of light.
- Snyder, Douglas (1997) A connection between gravitation and electromagnetism. American Physical Society, pp. 18-21.
- Poole G (2019) Electro dynamo theory of gravity (g). Journal of High Energy Physics, Gravitation and Cosmology 5(3): 773-789.
- Poole G (2019) Theory of electro relativity. Journal of High Energy Physics, Gravitation and Cosmology 5(4): 1063-1067.
© 2019 Greg Poole. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






