- Submissions

Full Text
Research in Medical & Engineering Sciences
Buckling of Osteoporotic Lumbar: Finite Element Analysis
Olga Chabarova1*, Rimantas Kačianauskas1 and Vidmantas Alekna2
1Department of Applied Mechanics, Lithuania
2Faculty of Medicine, Lithuania
*Corresponding author: Olga Chabarova, Department of Applied Mechanics, Lithuania
Submission: September 13, 2019; Published: September 20, 2019

ISSN: 2576-8816Volume8 Issue2
Abstract
Contribution of osteoporotic degradation to instability of lumbar spine is investigated by the finite element method. The aim of this work is to assess the biomechanical response of the osteoporotic L3 vertebrae under axial compression loading. The human lumbar spine segment comprising L2-L4 is considered. The anatomic shape of the patient-specific image-based geometry of lumbar vertebra is used for the three-dimensional finite element model. The cortical skin of vertebra id modelled by the shell, while cancellous tissue by the volume elements. The weak intervertebral discs are modelled as 3D composite. Three models including healthy and two trabecular bone osteoporotic degeneration cases are analyzed. The first case is restricted to osteoporotic degradation cancellous bone tissue as it is used in common praxis while the second case reflects limit situation when trabecular rarefaction occurs near the outer cortical shell. Numerical results of the non-linear finite element analysis showed that osteoporotic degradation is potentially suspicious for instability. The rarefication of cancellous bones yields to local buckling of vertebral wall essentially reducing load-bearing capacity, which has to be considered in such extreme situations. Consequently, the vertebra loses load-bearing capacity even when the strength limit is not reached. 3D finite element models were used. The aim of this work is to assess the biomechanical response, or load transfer response, between osteoporotic L3 vertebrae under compression loading. For this purpose, image-based, heterogeneous, three-dimensional, patient-specific finite element models of the lumbar vertebrae L3 for osteoporotic subjects were created. The finite element analysis has shown that local vertebral damage, such as empty spaces in vertebral bone, give rise to vertebral wall point’s horizontal displacement increase. Consequently, the vertebra loses load-bearing capacity even when the strength limit is not reached.
Keywords: Osteoporosis; Lumbar spine; Instability; FEM
Introduction
The key element of the human body is the spine, which provides the main support for mechanical behavior of the body, allowing to keep its functionality during the entire life period. Consequently, evaluation of the functionality of the spine requires knowledge about the mechanical behavior of the specified particular vertebra, which could be considered by applying research methods used in mechanics of solids and structures. From a mechanical point of view, the spine may be considered as a column-like structure consisting of relatively stiffer structural bodies, i.e. vertebrae, connected by flexible intervertebral discs. Thereby, the most loaded spinal fragment is the lumbar spine, i.e. the spine fragment composed of L1-L5 vertebrae, which has to bear the essential part of the human’s induced load compared to the other spinal parts [1-3]. Specifically, compression-induced fracture of the spine usually occurs at the third vertebra of the lumbar spine (L3) [4]. Mechanical behavior largely depends on mechanical properties. Mechanical properties of biological tissues are not constant, and they may be affected by various factories and disease. One of the most widespread disease is osteoporosis, which is characterized by an overall loss of bone tissue and is a systemic disorder of the skeleton, leading to enhanced fracture risk. It is estimated that up to 50% of females (30% for males) experience at least one osteoporotic vertebral fracture during their life [5,6]. Consequently, research on osteoporotic degradation is basically focused on evaluation of the change of mechanical properties in the vertebral bone tissue [7-9]. It was found, however, that macroscopic vertebral properties strongly correlate with bone density decrease. Therewith, bone mineral density (BMD) is probably the single directly measurable physical quantity.
Spine functionality could be characterized by values parameters and restrictions. Safe behavior is related to ability to withstand external loading. Despite remarkable progress in evaluation of mechanical properties of lumbar bone tissue on smaller scales [10], understanding of and the contribution osteoporotic changes to functionality is still not satisfactory. Evaluation of the failure risk is traditionally described by strength criteria in terms of stress-related parameters [6,11,12]. Alternatively, strength criteria of fracture may be expressed in terms of kinematic variables. Control of the deformation behavior by deformation criteria allows additionally to detect structure instability when the system undergoes large deformations. Instability is a process during which a given structure cannot sustain load in its initial form [13]. Finding deformation instability requires more enhanced nonlinear analysis. It is obvious that a vertebra looking like a stiffened cylindrical shell structure is potentially risky to instability. Mechanism of instability relevant to out-of-plane deformation of thin-walled structures is characterized as buckling-type instability. It is very sensitive to small deformations imperfections. During osteoporotic degeneration failure risk increases because of the thinning of the cortical shell and the presence of imperfections. Therefore, the load-bearing capacity of the spine may be lost, not only by fracture but also by the occurrence of instability. Consequently, osteoporotic imperfections may potentially produce increased fracture risks, which are different than those captured by the most commonly used strength criteria. The purpose of this investigation is to extend the knowledge on the macroscopic deformation behavior of the degenerated osteoporotic lumbar vertebrae by recovering geometric nonlinear deformation effects yielding instability of cortical shell. Mechanical study of osteoporotic lumbar L2-L4 fragment is presented in this paper. Here buckling of L3 vertebra is conceder numerically by applying finite element method. The emphasizes is giving to evaluation to of degraded bond between cortical shell and cancellous bone.
Problem Description
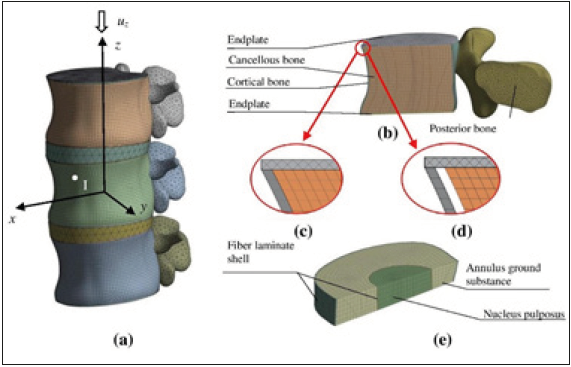
Evaluation of load bearing capacity osteoporotic L3 vertebra is studied. To avoid boundary effects related to transmitting of loading, a lumbar spine two-motion segments comprised by three L2-L4 vertebra connected by intervertebral disc (IVD) is considered (Figure 1a). IVD is composed of a nucleus pulposus, annulus fibrosus, and annulus ground substance. Disc’s model usually is separated between the nucleus, the annulus ground substance and annulus fibers. In the lumbar spine part, nucleus’ width is mostly between 30-50% of whole IVD cross-section width [14-16]. Posterior bony elements are added to reflect the stiffening of the vertebra’s back part. Two bony endplates are added to close a trabecular domain. From a mechanical point of view, essential properties of the vertebral body can be retained when regarding it in macroscopic scale as two-phase continuum. This two-phases-cortical shell and trabecular volume - model is mechanically reasonable and frequently explored in numerical modelling [10,17-20]. The issue of the above subdivision is slightly hypothetical. Classification of a particular sub volume to the cortical or trabecular phase could be done on the basis of CT imaging according to porosity (density) values [21]. Application of to phase model is especially advantageous in the case of osteoporotic degradation. The largest loss of absolute bone mass due to osteoporosis occurs in the bone interface layer between two phases [22]. The appearance of a gap between the two phases may be considered as an imperfection of potential instability factors. Each of spine models (Table 1) are subjected by compression load (Figure 1a). Three examples of spine fragment are different materials degeneration grade will be considering. The first model (Grade 1) reflects a healthy spine (Figure 1c), the second (Grade 2) reflects a loss in trabecular bone density (Figure 1c). Finally, the third model (Grade 3) will display the limit case of the bond weakened between the trabecular and cortical phases, as a result, the gap arises between the shell and the solid (Figure 1d). The data of three grades of normal aging degeneration process from healthy to degenerated case are seen in Table 1.
Materials and Methods
Problem geometry
The lumbar spine two-motion segment of the anatomic shape shown in Figure 1 is considered. The lumbar body is described in Cartesian coordinates. The coordinate plane Oxz is symmetry plane of the body. The trabecular volume is considered as a three-dimensional continuum while the dense cortical layer is considered as a thin shell. The geometry and dimensions of the model were obtained from a high-resolution CT images. The images were reconstructed with a 0.3mm slice thickness and exported as DICOM files.
Figure 1:View of the models. (a) Lumbar spine model of two spinal motion segment with (L2-L4), (b) L3 vertebra’s cross-section FE model, (c) Bonded connection, (d) Unbonded connection with a gap, (e) IVD cross section FE model.
Mechanical properties
The cortical phase is modelled as an isotropic elastic continuum. The trabecular phase is modelled as an elastic orthotropic continuum. Thereby, the transverse elastic modulus is assumed to be the fraction of the longitudinal modulus. The posterior bony elements and endplates are described as linear elastic isotropic material. Osteoporotic ageing degeneration properties will be different for each model. They are giving in Table 1. Vertebral bones material physical properties are seen in Table 2.
Table 1:Characterization of age-related degeneration.

Table 2:Material properties of the components.

Finite element model
In this study, the numerical finite element analysis is utilized to demonstrate the potential of this tool in evaluation of the risk of osteoporotic degradation. Particular advantages of the finite element analysis will be explored by developing a universal finite element model able to solve various mechanical problems using the same geometry. On the other hand, the unified model integrates the external shell and the internal 3D solid while regarding different bonding between them. A characterization of the mechanical state of lumbar vertebrae under osteoporotic degeneration of bone tissues will be considered by structural analysis, thereby applying the finite element method. Three different finite element models describing the above-mentioned samples Grade 1, Grade 2, Grade 3 are created modeling purposes. Cortical bone was discretized by shell finite elements. A shell element associated with larger strain and large deflection is sable to describe structure buckling. The FE mesh of cortical shell contains 9669 nodes and 9367 shell elements. A cancellous bone, endplates, posterior bone, nucleus pulposus and annulus ground substance models were meshed with volumetric FE. The element supports large displacement and large strain capabilities. The volumetric phase was described by a 3D mesh containing 710751 nodes and 188100 solid elements. Shell and volumetric domains are connected with a rigid bond according to Table 1. Fragment of bonded and unbonded connections are illustrated in (Figure 1c & 1d), respectively. IVD and NP are covered by fiber-reinforced membrane. The thickness of the membrane is to 1.5mm. The membrane is composed by four layers of fiber laminate, which are stacked by +30° and -30° plies. This study used composite four-node shell elements to simulate annulus fibrous. Here, bending stiffness is neglected and only in-plane behavior is considering. The FE mesh of fiber laminate contains 358 nodes and 416 shell elements. The meshed model is presented in Figure 1e.
Analysis problem
Development of the FE model comprises mathematical description of the lumbar spine and generation FE assembly. The time-dependent state of the spine two-motion segment is obtained by formulating the nonlinear analysis problem. The behavior of the FE model is governed by kinematic boundary conditions. The time-dependent state of the vertebral body is obtained by formulating the nonlinear analysis problem. The behavior of the finite element model is governed by kinematic boundary conditions. Zero motion is specified on the bottom L4, while proportionally increasing loading is imposed by the vertical motion of the upper endplate L2 with the maximal vertical displacement uz(t). Thus, external axial loading in time t is controlled by the instantaneous contribution of the displacement. The axial loading is controlled by the specified monotonically increasing displacement of the upper endplate uz(tmax )=uz,max limited by maximal value uz,max=10mm. The load is transmitted to the trabecular and cortical bones through an endplate.
In summary, the nonlinear loading-path-dependent equilibrium is characterized by a set of nonlinear algebraic equations. The incremental formulation of this model is defined at time instant t as follows:
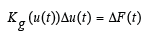 (1)
(1)
Here, KG is the global nonlinear stiffness matrix comprising contribution of the finite displacements and depending on current values of the displacement vector u(t), while Δu and ΔF are increments of displacement and external load vectors, respectively. The stresses are obtained for values displacements of each element separately [23-35]. Here, an augmented Lagrangian approach was applied for handling the inequality constraints in the solution of the contact problems. Actually, in order to find a bifurcation point and to trace a descending loading branch during instability of loading prescribed displacements are specified. The discretization of the bodies is performed by applying the preprocessor of the ANSYS code [36].
Numerical Results and Discussion
To evaluate degrees of osteoporotic degradation, numerical experiments were performed using the Eq. (1). Three models of the lumbar spine were solved. Presentation of numerical results is limited by discussion of L3 vertebra. Physical nature of different models is qualitatively illustrated by deformation behavior. Deformed shapes of cortical shell occurring at the end of simulations at time instants tmax are shown in Figure 2. The first subfigure (a) illustrate healthy vertebra, the second subfigure (b) illustrate osteoporotic vertebra with bonded shell-solid interface, while the third subfigure (c) illustrate unbonded contact-less situation. The colored contour plot illustrates of displacement magnitude in unified scale. The displacement values are defined in millimeters. It was observed, that healthy example (Grade 1) has the most rigid properties, and it is characterized by the smallest displacements (Figure 2a). In comparing to that, degradation of cancellous tissue (Grade 2) yields large displacements, retaining, however, simile deformed shape (Figure 2b). Degradation of the cortical shell (Grade 3) leads to more complex deformation shape where local imperfections are clearly observed (Figure 2c). It was observed for healthy sample the larges transversal displacement occurred in point I, which located in central symmetry plane at the height 20mm. Therefore, transversal displacement uI will for detail analysis.
Figure 2:The view of deformed shapes of L3 cortical shell and contour plot of displacement magnitude (mm) after loading at time instant tmax: a)-Grade 1; b-Grade 2; c-Grade 3.

Essential properties of the compressed anatomic cylinder may be characterized explicitly by the force-displacement F(t)– u(t) relationship. This relationship between axial force and displacement components ux at point I (Figure 3) will be used explains stability properties. The first curve, denoted as Curve a, illustrate deformation behavior of healthy vertebra (Figure 4). The healthy sample exhibit monotonic increasing for displacement character indicating stable deformation behavior. The next Curve b analogously illustrate the osteoporotic degradation of lumbar vertebra in the case of perfect bonding with shell. This curve demonstrates the global post buckling instability at point D where critical load F2,cr=8.0 kN. Therefore, when compressing a degenerated lumbar, the time history of the transversal displacement at point I (Figure 3) exhibits unlimited character, illustrating unstable deformation behavior. The third Curve c illustrate the variation of these quantities for the case of degenerated bond. The descending character of displacement from point A to point B and above point C indicates unstable deformation. The variation of displacement Figure 3 clearly shows the presence of a critical point instant u3,cr F3,cr=0.06mm. Consequently, load-bearing capacity is predefined by the critical buckling load F3,cr=2.1 kN (Figure 3). The load-carrying capacity of the spine, in over case of lumbar is usually characterized by force values. In the column diagram (Figure 4) is the variation of maximum compression forces is shown. The first column indicates the maximum value F1=9.0kN of heathy case. This force was reached maximum compression displacement 10mm. Considering the load-displacement path (Curve a in Figure 3), the further the increasing of this load is expected. By considering osteoporotic degenerated lumbar (Grade 2), load-bearing capacity drops and is characterized by critical load Fcr,2=8.0kN. In the third sample, the critical load Fcr,3=2.1kN denoted in Figure 3 at point A is achieved at an early state. Compared to available experimental data [37,38], where carrying load Fcr=15.9kN is estimated for the young man, the significant contribution of osteoporotic degradation was observed. The performed numerical stability analyses of lumbar vertebrae discovered that the presence of local degradation between cortical and trabecular bones may yield catastrophic consequences in the mechanical behavior of lumbar vertebrae. Consequently, specific testing procedures have to be elaborated to prevent acquiring dangerous osteoporotic degradation, especially due to rarefication of bone tissue near the cortical wall.
Figure 3:Load dependency graph. Displacement in horizontal direction at point I (Figure 2).

Figure 4:Comparison of forces for compression versus age-related degeneration.

Conclusion
Numerical simulation illustrating the contribution of osteoporotic degradation of mostly loaded spine lumbar vertebra L3 results is presented. Three cases of vertebra properties were considered, comprising healthy, osteoporotic, reflecting a loss in trabecular bone density, and the third limiting case, reflecting off the bond weakened between the trabecular and cortical phases. Simulation results discovered deformation instabilities occurring with osteoporotic degeneration of the cancellous bone tissues. In summary, it could be concluded that osteoporosis of the lumbar vertebrae yields to reduction of the safe load. The critical reflecting stability finally drops below the presumed strength threshold value. Consequently, to determine risk of fractures the local deformation criteria including the buckling should be applied. To detect buckling-induced risk, it is mandatory to evaluate not only average trabecular bone density, but also degradation regions near the cortical shell.
References
- Dicko AH, Tong Yette N, Gilles B, François Faure, Olivier Palombi (2015) Construction and validation of a hybrid lumbar spine model for the fast evaluation of intradiscal pressure and mobility. International Journal of Medical and Health Sciences 9(2): 134-145.
- Du HG, Liao SH, Jiang Z (2016) Biomechanical analysis of press-extension technique on degenerative lumbar with disc herniation and staggered facet joint. Saudi Pharmaceutical Journal 24(3): 305-311.
- Su X, Shen H, Shi W, Yang H, Lv F, Lin J (2017) Dynamic characteristics of osteoporotic lumbar spine under vertical vibration after cement augmentation. Am J Transl Res 9(9): 4036-4045.
- Jiang Y, Lin D, Guo X (2018) AB1017 Vertebral fractures are likely to occur in lumbar vertebra in patients with osteoporosis and even in osteopenia. BMJ 77(2): 1627-1627.
- Briggs AM, Wrigley T V, Van Dieën JH, Phillips B, Lo SK, et al. (2006) The effect of osteoporotic vertebral fracture on predicted spinal loads in vivo. European Spine Journal 15(12): 1785-1795.
- Kim YH, Wu M, Kim K (2013) Stress analysis of osteoporotic lumbar vertebra using finite element model with microscaled beam-shell trabecular-cortical structure. Journal of Applied Mathematics 5: 1-6.
- Badilatti SD, Kuhn GA, Ferguson SJ, Müller R (2015) Computational modelling of bone augmentation in the spine. Journal of Orthopaedic Translation 3(4): 185-196.
- Maquer G, Schwiedrzik J, Huber G, et al (2015) Compressive strength of elderly vertebrae is reduced by disc degeneration and additional flexion. Journal of the Mechanical Behavior of Biomedical Materials 42: 54-66.
- Tsouknidas A, Maliaris G, Savvakis S, Michailidis N (2015) Anisotropic post-yield response of cancellous bone simulated by stress-strain curves of bulk equivalent structures. Comput Methods Biomech Biomed Engin 18(8): 839-846.
- Blanchard R, Morin C, Malandrino A, Vella A, Sant Z, et al. (2016) Patient-specific fracture risk assessment of vertebrae: a multiscale approach coupling X-ray physics and continuum micromechanics. Int J Numer Method Biomed Eng 32(9): 1-36.
- Ghadiri M (2014) Fracture mechanics analysis of fourth lumbar vertebra in method of finite element analysis. Int J Adv Biol Biom Res 2(7): 2217-2224.
- Takano H, Yonezawa I, Todo M (2017) Biomechanical study of vertebral compression fracture using finite element analysis. JAMP 5(4): 953-965.
- Loughenbury PR, Tsirikos AI, Gummerson NW (2016) Spinal biomechanics-biomechanical considerations of spinal stability in the context of spinal injury. Orthopaedics and Trauma 30(5): 369-377.
- Zhang F, Zhang K, Tian HJ, Wu AM, Cheng XF, et al. (2018) Correlation between lumbar intervertebral disc height and lumbar spine sagittal alignment among asymptomatic Asian young adults. J Orthop Surg Res 13(1): 13-34.
- Teichtahl AJ, Finnin MA, Wang Y, Wluka AE, Urquhart DM, et al (2017) The natural history of modic changes in a community-based cohort. Joint Bone Spine 84(2): 197-202.
- Teichtahl AJ, Urquhart DM, Wang Y, Wluka AE, Heritier S, et al (2015) A Dose-response relationship between severity of disc degeneration and intervertebral disc height in the lumbosacral spine. Arthritis Research & Therapy 17(297): 1-6.
- Okamoto Y, Murakami H, Demura S, Kato S, Yoshioka K, et al (2015) The effect of kyphotic deformity because of vertebral fracture: a finite element analysis of a 10° and 20° wedge-shaped vertebral fracture model. The Spine Journal 15(4): 713-720.
- Zhu R, Niu WX, Zeng ZL, Tong JH, Zhen ZW, et al (2017) The effects of muscle weakness on degenerative spondylolisthesis: A finite element study. Clinical Biomechanics 41: 34-38.
- Kinzl M, Schwiedrzik J, Zysset PK, Pahr DH (2013) An experimentally validated finite element method for augmented vertebral bodies. Clinical Biomechanics 28(1): 15-22.
- Lan C, Kuo C, Chen C, Hu H (2013) Finite element analysis of biomechanical behavior of whole thoraco-lumbar spine with ligamentous effect. The Changhua Journal of Medicine 11: 26-41.
- Hamilton EJ, Ghasem Zadeh A, Gianatti E (2010) Structural decay of bone microarchitecture in men with prostate cancer treated with androgen deprivation therapy. The Journal of Clinical Endocrinology & Metabolism 95(12): E456-E463.
- Zebaze RM, Ghasem Zadeh A, Bohte A (2010) Intracortical remodelling and porosity in the distal radius and post-mortem femurs of women: a cross-sectional study. The Lancet 375(9727): 1729-1736.
- Chabarova O, Alekna V, Kačianauskas R, Ardatov O (2017) Finite element investigation osteoporotic lumbar L1 vertebra buckling in a presence of torsional load. Mechanics 23(3): 326-333.
- Finley SM, Brodke DS, Spina NT, DeDen CA, Ellis BJ (2018) FEBio finite element models of the human lumbar spine. Computer Methods in Biomechanics and Biomedical Engineering 21(6): 444-452.
- Polikeit A, Nolte LP, Ferguson SJ (2004) Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. Journal of Biomechanics 37(7): 1061-1069.
- Jones AC, Wilcox RK (2008) Finite element analysis of the spine: Towards a framework of verification, validation and sensitivity analysis. Medical Engineering & Physics 30(10): 1287-1304.
- Monteiro NMB, Silva MPT, Folgado JOMG, Melancia JPL (2011) Structural analysis of the intervertebral discs adjacent to an interbody fusion using multibody dynamics and finite element cosimulation. Multibody System Dynamics 25(2): 245-270.
- Zahaf S, Habib H, Mansouri B (2016) The effect of the eccentric loading on the components of the spine global journal of researches in engineering: a mechanical and mechanics engineering the effect of the eccentric loading on the components of the spine. Global Journals Inc 16(4): 2249-4596.
- Alkalay RN, Harrigan TP (2016) Mechanical assessment of the effects of metastatic lytic defect on the structural response of human thoracolumbar spine. Journal of Orthopaedic Research 34(10): 1808-1819.
- Charosky S, Moreno P, Maxy P (2014) Instability and instrumentation failures after a PSO: a finite element analysis. European Spine Journal 23(11): 2340-2349.
- Ng H, Teo E, Lee V (2004) Statistical factorial analysis on the material property sensitivity of the mechanical responses of the C4-C6 under compression, anterior and posterior shear. Journal of Biomechanics 37(5): 771-777.
- Fan R, Gong H, Qiu S, Zhang X, Fang J, et al (2015) Effects of resting modes on human lumbar spines with different levels of degenerated intervertebral discs: a finite element investigation. BMC Musculoskeletal Disorders 16(221): 1-15.
- Niemeyer F, Wilke HJ, Schmidt H (2012) Geometry strongly influences the response of numerical models of the lumbar spine-A probabilistic finite element analysis. Journal of Biomechanics 45(8): 1414-1423.
- Panzer MB, Cronin DS (2009) C4-C5 segment finite element model development, validation, and load-sharing investigation. Journal of Biomechanics 42(4): 480-490.
- Chen WM, Jin J, Park T, Ryu KS, Lee SJ (2018) Strain behavior of malaligned cervical spine implanted with metal-on-polyethylene, metal-on-metal, and elastomeric artificial disc prostheses - A finite element analysis. Clinical Biomechanics 59: 19-26.
- Madenci E, Guven I (2015) Fundamentals of Discretization the finite element method and applications in engineering using ANSYS®. Springer, USA, pp. sss35-74.
- Crawford RP, Keaveny TM (2004) Rela thoracolumbar vertebra. Spine 29(20): 2248-2255.
- Hutton WC, Cyron BM, Stott JR (1979) The compressive strength of lumbar vertebrae. Journal of Anatomy 129(4): 753-758.
© 2019 Olga Chabarova. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






