Enhancing Radical-Mediated Photopylomerization Efficacy and Crosslink Depth: Kinetic Modeling of a Two-Monomer System

Photopolymerization and crosslinking have been utilized in various medical and industrial applications [1-5]. Comparing to thermal-initiated polymerization, photo-initiated polymerization provides advantages of fast and controllable reaction rates, and spatial and temporal control over the formation of the material, without the need for high temperatures or harsh conditions [1,2]. Tissue-engineering using scaffold-based procedures for chemical modification of polymers has been reported to improve its mechanical properties by crosslinking or polymerization with UV or visible light to produce gels or high-molecularweight polymers [3]. Industrial applications include the develop of materials for thin films, 3D bio-printing and microfabrication [4-7], in which he kinetics and mechanisms of photopolymerization have been extensively studied theoretically and experimentally [7-16]. Conventional photopolymerization involves with a single-monomer system having either one or more initiators. Two-monomer systems were also reported such as: (i) thiol-ene system (TES), and (ii) thiol--Michael system (TMS); where in TES, cross-linked polymer networks are formed via a two steps growth mechanism:

1. Propagation of a thiyl radical through a vinyl functional group; and

2. Followed by chain transfer from the resulting carbon radical to a thiol functional group, regenerating the thiyl radical [16-21]. In comparison, TMS involves anion-mediated additions of a multifunctional thiol to an electron-deficient vinyl group of a multivinyl component [22-25]. Both TES and TMS exhibit the advantages of typical photopolymerizations including rapid, optically clear, negligible oxygen inhibition, solvent tolerance, high reaction yields, excellent mechanical properties and do not require solvents for processing [17].

Both computational and experimental investigations have been performed to evaluate the role of solvents, monomers, and catalysts on the reaction mechanism [12-25]. However, most of the previous models [18-15] are based on oversimplified assumptions of constant photoinitiator (PI) or photosensitizer (PS) concentration (without depletion), and thus the light intensity follows the conventional Beer-Lambert law (BLL), which are only valid for optically-thin polymers and will suffer huge errors in optically-thick polymers [12-14]. We have previously considered a one-monomer system for a UV light induced crosslinking (UVX), in which type-I is the predominant process [5,10,11]. In contrast, an oxygenmediated type-II process, where the single-monomer radical induced type-I conversion is not very efficient. Therefore, additive enhancer-monomer, or co-initiator is needed for improved overall (type-I plus type-II) efficacy [26]. The kinetic of a one-monomer system using UVA and riboflavin have been reported [5,10,11]. We have also reported a one-monomer, but two-initiator system, in which the coversion effeicacy is enhanced by the co-initiator in a type-II predominant prosses [15]. This article will present, for the first time, a two-monomer system, consisting of monomer-A and monomer-B. Temporal prpfiles of the monomer efficacy and cosslink depth, as a function of light intensity, exposure time, and concentrations of PI, [A] and [B]. Furthermore, the scaling laws for the crosslink depth and efficacy will be explored and compared with measurements. The measured results of Wertheimer et al [26] will be analyzed, in which the efficacy may be enhanced by an enhanceintiator or increase the lifetime of photosensitizer triplet-state, or oxygen singlet-state, in the presence of D2O. The oxygen inhibition effect and homopolymerization side-effect are also included in this study, such that the co monomers [A] and [B] cover a wider range of suitable materials; whereas they are neglected in TES and TMS, which requires a specific functional group of ene.

Photochemical Kinetics

Figure 1:Schematics of 3 photochemical pathways in a two-initiator system [15], PS and PB, in the presence of oxygen O2, for radical-mediated pathways (1 and 2), and oxygen-mediated pathway (3); where PS is excited to an excited state (Ps*) and a triplet state (T*).-

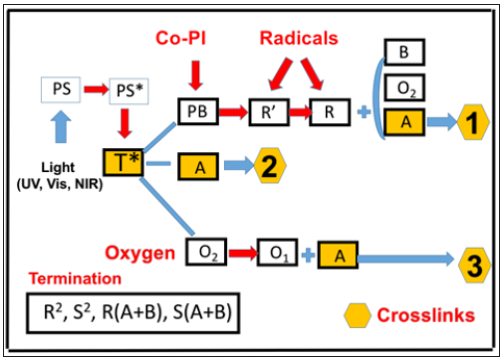
As shown by Figure 1, a two-initiator, PS and PB, system [15] involves 3 crosslinking pathways: two radical-mediated (or electron transfer) pathways (1 and 2), and one oxygen-mediated (or energy transfer) pathway (3). The ground state photosensitizer (PS), is excited to its triplet excited state T* by a quantum yield (q). In a type-I process, T* interacts directly with the substrat [A] or to form the first radicals R’ and S’, then produce the reactive intermediates radicals, R and S, which could interact with oxygen [O₂], [A], PS or PB, or bimolecular termination. For a type-II (or oxygen-mediated) process, T* interacts with [O₂] to form a singlet oxygen [O₂] which could interact with [A], PB or relaxed to [O₂].

Figure 2:Schematics of a two-monomer system 6, A and B, in the presence of oxygen O2, for radical-mediated pathways (1 and 2), and oxygenmediated pathway (3); where PS is the ground state photosensitizer, having an excited and triplet state PS* and T*.

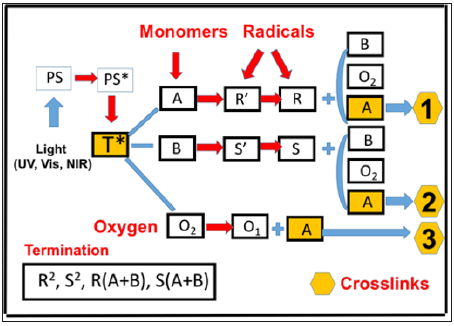
In comparison, as shown by Figure 2, a two-monomer (A and B) and one-initiator (PS) system, which involves 3 crosslinking pathways: two radical-mediated (or electron transfer) pathways (1 and 2), and one oxygen-mediated (or energy transfer) pathway (3). The ground state photosensitizer (PS), is excited to its triplet excited state T* by a quantum yield (q). In a type-I process, T* interacts directly with [A] and [B] to form the first-radicals R’ and S’, then produce the reactive intermediates R and S which could interact with oxygen [O₂], [A], [B], or bimolecular termination. For a type- II (or oxygen-mediated) process, [T] interacts with [O₂] to form a singlet oxygen [O1] which could interact with [A], [B], or relaxed to [O₂]. Both type-I and type-II reactions can occur simultaneously in photopolymerization and the ratio between these processes depends on the type of photosensitizer (PS) or photoinitiator (PI) used, the concentrations of PS or PI, substrate monomers and oxygen, the kinetic rates involved in the process, and the light intensity, dose, PI depletion rate etc. Greater detailed kinetic of was published in our prior work [10]. We note that the thiol-ene systems (TES) [16,17] are the special situation of the more general pathway of Figure 2, where the functional groups are insensitive to the oxygen inhibition and can be treated as a type-I dominant system, with neglected oxygen-mediated type-II. Therefore, the rate equations for thiol-ene system is simplified. In addition, thiol monomer, [B], does not coupler directly with thiyl radical (R’), but with the carbon radical (R) to regenerate R’ which reacts with [A] to form the reaction cycle [16]. In the cycle scheme, the sum of (R+S) is assmed to be a constnat, in which the total rate function can be simplified. In this study we will only use the quasi-steady state conditions for R’, R, S’ and S, without the assumption of the cyclecondition. The oxygen inhibition effect and homopolymerization side-effect given by the coupling of S and [B] are also included in this study, such that the co monomers A and B cover a wider range of suitable materials; whereas they are neglected in TES, which requires a specific functional group of ene.

The kinetic equations for our previous 1-monomer system [11] are revised for a 2-monomer ([A] and [B]) system. For comprehensive modeling we will use the so-called quasi-steady state assumption [5] described as follows. The lifetime of triplet states of PS, the radicals (R’, R, S and S’), and the singlet oxygen (X) are very short (ns to μs time scale) since they either decay or react with cellular matrix immediately after they are created. Thus, one may set dT*/dt=dX/dt=dR’/dt=dS’/dt=0. Under these quasisteady- state conditions, we obtain [11,15]

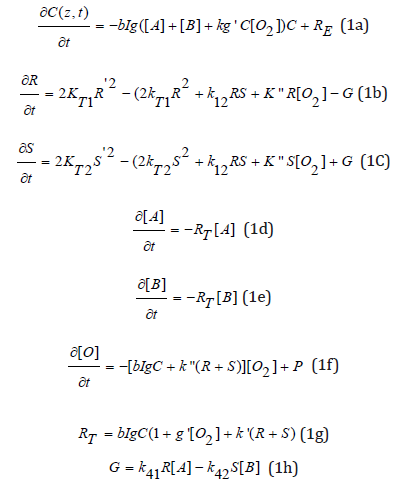
where g=1/(k₅₇+k₃₇[O₂] +[A]+ [B]), g’=1/ (k₆₈+ k₄₈C+ [A]+ [B]), k=(k₁₁/k_{8); k37 = k3/k7, k57 = k5/k7; k68 = k6/k8, k48= k4/k8. RE is the regeneration of PI ground state given by RE=k”(R+S)[O2].}

b=83.6a’wq, with w being the UV light wavelength (in cm) and q is the triplet state [T] quantum yield; a’ in (1/mM/%) and I (z,t) in mW/cm². In a UVX system, b=0.62q, for UV light at 365nm (with a’=204 (1/mM/%), which has a penetration depth of 150 to 190um [8]. For aose Bengal system with a green light, the b value is approximately 4 time larger and having a smaller penetration depth of 100um [26]. Eq. (1.f) also includes an oxygen source term given by P=(1-X/X₀) P₀, with a maximum rate constant P₀ [5]. All the reaction rate constants are defined by the associated coupling terms. For examples, k71 is for the reaction of [A] and T, which has a ground state relaxation rate k₅; R is coupled with R’ by k₁₂, and coupled with oxygen by k, having a bimolecular termination rate of k_T. Greater detail and derivation of above equations may be found in Ref. [15], which also shows the kinetic equations for the triplet state (T*) and singlet oxygen [X]. In deriving Eq. (1), we have used the steady-state triplet state (T*) and singlet oxygen [X] given by [15]: T*=bIgC/k₇, and [X]=bIg’C/k₈. We note that Eq. (1.d) and (1.e) reduce to that of TES [16], when the homopolymerization terms, R[A] and S[B] are neglected in Eq. (1.d) and (1.e), respectively; and TES also assumed d[A]/dt=d[B]/dt, such that R is related to S, and Eq. (1.d) and (1.e) have a different total rate function, i.e., d[A]dt=- (KR)[A], and d[B]/dt=-(KS)[B], whereas our formulas give d[A]/ dt=R_T[A] and d[B]/dt=R_T[B], sharing a common R_T.

The radicals, R’ and S’, are given by their steady-state solutions given by R’= (bICg [A]/k_Tsub>)^0.5, and S’= R’[B]/[A]. Using these R’ and S’, we may find the steady-state solution of Eq. (1b) and (1c) given by, when k₁₂RS and G are ignored in Eq. (1b), (1c),

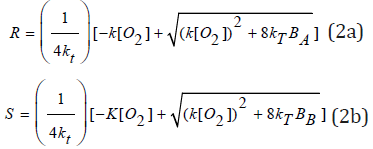
where B_A =bICg[A] and B_B=B_A[B]/[A].

The dynamic light intensity is given by [12,13,15]

a’ and b’ are the extinction coefficients of PS and the photolysis product, respectively; Q’ is the absorption coefficient of the stroma at UV (365nm) or green (532nm) wavelength.

Conversion Efficacy

Numerical solutions are required for Eq. (1) and (3). However, analytic formulas are available for (k[O₂])₂ <<8kT[B], and Eq. (2) is given by its Tylor expansion, thus Eq. (1) reduces to

where K₂₃= k’k/k_T; RE=(kK₁₃/k’)[O₂], R=[0.5bIC/(k_T(1+[B]/ [A])]^0.5, K₁₃ is given by the Taylor expansion of Eq. (2) with R’=S’ (or g[A]=g[B]). Where we have defined a total rate function (R_T) for the monomer conversion consisting of three parts: the coupling of [A] with the triplet-state (the first term bIgC), the singlet oxygen (K₁₂ term), and the radicals R’ and S’ (K₁₃ term). Furthermore, K13 consists of the radical formation and the quenching effect due to oxygen, the second term of Eq. (4.e).

The conversion efficacy of monomer [A] is defined by C_A=1- [A]/[A]₀=1- exp(-S), where the S function is given by the time integral of the total rate function, RT, given by Eq. (5.e). For the type-I predominant case with [A]>>K₁₁[O₂], R_E, in Eq. (5.a), we have previously developed approximated analytic formulas for I(z,t) and C(z,t) as follows [12,13]

where B’=bI₀exp(-A”z), A₁=2.3(a’-b’)C₀I₀bz, with A” is the averaged absorption given by A”=1.15(a’+b’)+2.3Q. We note that the –A₁t term represents the decrease of A’ or increase of light intensity due to the PS depletion.

Numerical solution of Eq. (4) and (5) will be shown later. Using Eq. (5), analytic solution of Eq. (4.c) and the S-function are available when K₂₃[O₂] is neglected and [B]<<[A], g[A]=1, such that R_T=k’R’=k’(0.5bIC/k_T)0.5. Time integral of RT gives the S-function, noting that the efficacy is related to S by [12] C_EFF=1-exp(-S),

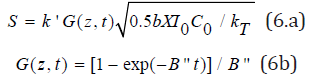
where B”=0.5(B’- A₁), X=exp[-zA₂], with A₂=1.15(a’+b’) C0+2.3Q. We note that Eq. (6.b) defines the dynamic feature of the light intensity which is an increasing function of time due to the depletion of the RF concentration. It also provides the nonlinear dynamic dependence of A’(z,t), given by A1t, which is important for optical-thick system and for high light dose.

To discuss the role of the lifetimes of the triplet-state (T₁) and singlet-oxygen (T₂), Eq. (4) may be expressed by as follows:

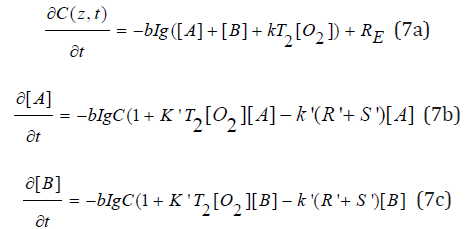
where g=k₇T₁, K=k₁₁(k₃/k₇), K’=k8(k₃/k₇). We note that g([A]+[B]) can be expressed as g=[1-(k₃/k₇)[O₂]/[AB]/[AB], with [AB]=[A]+[B]., which shows the oxygen inhibition effect is proportional to the ratio (k₃/k₇)[O₂]/[AB].

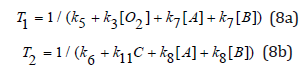
Crosslink depth (ZC) and Crosslink time (TC)

A crosslink depth (ZC) and crosslink time (TC) are defined by when the efficacy reaches a threshold value (CT) at a depth t and z. Using Eq. (7), and let S= ST=2 (or CEFF=0.86), ZC is related TC by

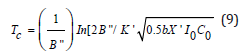
where K’= k’/kT_0.5, X’=exp(-A”ZC). Eq. (11) is a nonlinear equation of ZC which can be numerically plot by rotating the curve of TC vs ZC to show the curve of ZC vs TC (to be shown later).

Numerical results

Numerical solutions of Eq. (4) will show the role of each of the key parameters on the profiles of RB and oxygen concentration, and the efficacy of monomer-A defined by C_A=1-[A]/[A]0. They include: light intensity (I₀) the rate constants (k’ and k₃₇), initial concentration of [A], [B], and various depth (z).

Figure 3 shows the role of light intensity (I₀), in which higher I0 leads to faster depletion of PS and oxygen concentration; and faster transient rising efficacy, but a lower steady-state efficacy, as shown by Figure 2-(c), as also predicted by our S-formula of Eq. (6), which has a steady state value (when G=1) scaled by (C₀/ I₀)^0.5. Figure 4 shows the role of the radical coupling rate constant (k’), in which larger k’ leads to higher efficacy, as also predicted by Eq. (6a). Figure 5 shows the role of the rate constant ratio of oxygen-substrate (k₃) and triple-state-substrate (k₇), k₃₇=k₃/k₇, in which higher ratio leads to lower efficacy resulted by the stronger oxygen inhibition, as predicted by our formula of Eq. (4e), in which g-factor is a decreasing function of k₃₇. Figure 6 shows the efficacy at various depth (z), in which RB and oxygen have faster depletion on the stroma surface (z=0) than inside the stroma; and surface has a higher efficacy in transient state; but lower efficacy at steady-state; an opposite trend comparing to efficacy versus light intensity, as also predicted by our formula of Eq. (6), in which X=exp[-zA₂] is a deceasing function of z. Figure 7 shows the role of the initial concentration ratio [B]₀/[A]₀, in which higher ratio (for a fixed [A]₀) leads to higher efficacy resulted by the additive enhancer-monomer-B, as also predicted by Eq. (4f). However, an opposite trend is shown in Figure 8, for the reverse ratio of [A]₀/ [B]₀, for a fixed [B]₀. Figure 9 shows that the crosslink depth (ZC) is a nonlinear increasing function of light intensity and exposure time, i.e., higher dose provides a deeper ZC, as predicted by formula of Eq. (9). As shown by Figure 10, ZC is also an increasing function of RB concentration, scaled by ln(C₀/I₀)^0.5, which may be derived from the steady-state of Eq. (6). This concentration scaling was also reported clinically [11]. We note that ZC also proportionally related to the measured demarcation depth, which shows a creasing function of light intensity for a fixed light dose.

Figure 3:The temporal profile (normalized by its initial value) of RB, oxygen and the conversion efficacy of monomer-A (on stroma surface, z=0); for light intensity I₀ = (100,200,300,400)mW/cm², for curves (1,2,3,4); for C₀=1.0mM, A₀=500mM, B₀=100mM; b=0.00046, k’=150, k_T=150, k₃₇=0.5, k₅₇=0.1, k₁₈=1.0, k_T=1.0, k=10 (1/ mM/s).

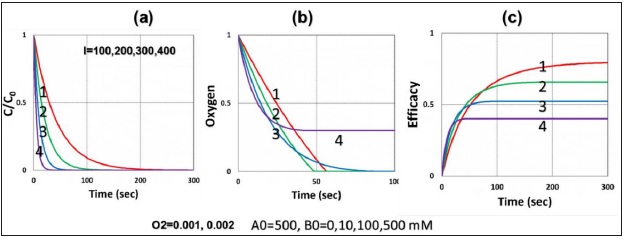
Figure 4:Same as Figure 2 but comparing the radical coupling rate constant of: (a) k’=150, and (b) k’=100 (1/M/s), for various light intensities.

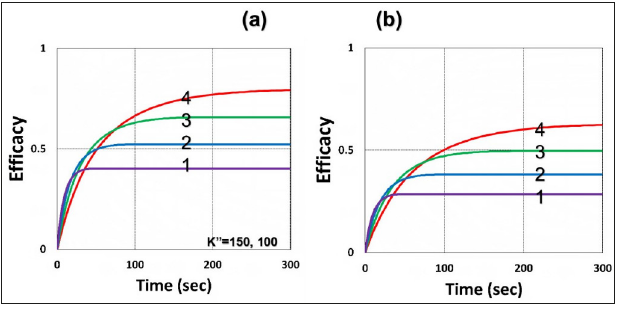
Figure 5:Same as Figure 2 but comparing the rate constant ratio of oxygen (k₃) and substrate (k₇) for k₃₇=k₃/k₇ = (0.5, 5.0, 25, 100), for curves (1,2,3,4); light intensity I₀ = 100mW/cm².

Figure 6:Same as Figure 2, but for efficacy on stroma surface (z=0), and inside the stroma, (z>0); for z= (0, 200l 400, 600)m, for curves (1,2,3,4), with I₀=100mW/cm².

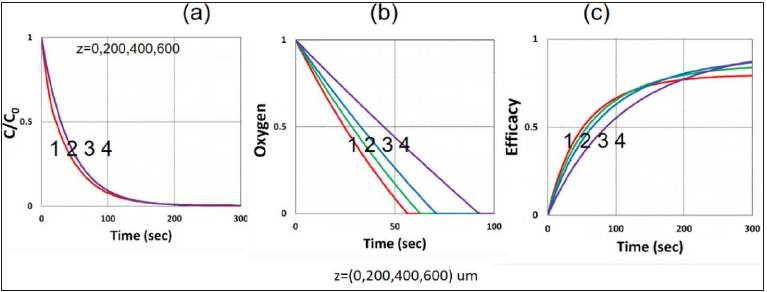
Figure 7:Same as Figure 2, but for various monomer-B initial concentration B₀= (0,10,100, 500)mM, for curve (1,2,3,4), with fixed A₀=500mW, and I₀=100mW/cm².

Figure 8:Same as Figure 6, but for various A₀= (1, 100, 250, 500)mM, for curve (1,2,3,4), for fixed B₀=100mM, I0=100mW/cm².

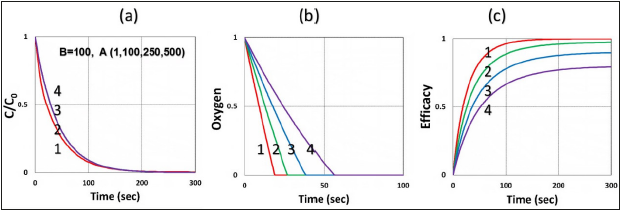
Figure 9:Crosslink depth (ZC) vs. light intensity (I₀) for t= (60,300,600)s, for curves (1,2,3); for C₀=0.1%.

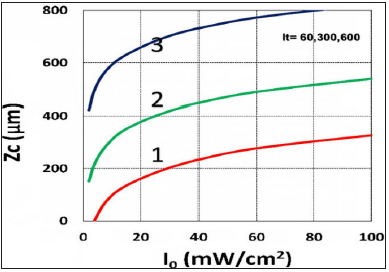
Figure 10:Crosslink depth (ZC) vs. time, for C₀= (0.1, 0.2, 0.3,0.4)%, for curves (1,2,3,4); for I₀=10W/cm².

Analysis of Efficacy

Eq. (4) defines the total conversion rate (RT) of monomers, which has three parts contributed by: (i) coupling of [A] or [B] with the triplet-state (T*), (ii) coupling of oxygen with the triplet-state (T*) producing the singlet oxygen, and (iii) coupling of [A] or [B] with the the radicals R’ and S’ (the K13 term). As shown by Eq. (7b) and (8), RT proportional to the lifetimes T1 (for triplet state), and T₂ (for singlet-oxygen), oxygen concentration, [O₂], and the rate constants (kj).

The results of Figures 3-10 are summarized as follows:

a) Our formulas, Eq. (4e) and (4f) show that a system is type-I or type-II predominated depending on a ratio RA =K₁₃/ (BK₁₂[O₂]). When RA>0.8, type-I is predominant, whereas type-II is predominant, for RA<0.2 (or for large singlet-oxygen rate constant, k₃₇k₈). In general, both type-I and type-II co-exists initially (with RA having a value of 0.5 to 1.5), until oxygen is depleted (or when k₃₇k₈[O₂] =0).

b) For UV crosslink (UVX) system, with R_A>0.9, as proposed by and Lin [12] that CXL is predominated by type-I, which does not require oxygen; in contrast to a type-II oxygen-mediated system. The type-I conversion efficacy, given by C_A=1-exp(-S), with S is the time integral of RT, and has a state-state scaled by [C/(bI)]^0.5, for a bimolecular termination process. In the UVX system, the oxygen inhibition effect reduces the lifetime, as shown by Eq. (8a) with T₁=g/ k₇= (1- R_D)/([A]+[B]), having a reduction factor R_D=(k₅₇+k₃₇[O₂])/ ([A]+[B]), and thus reduces the conversion efficacy of [A]. Another factor reducing the efficacy is given by the second term of Eq. (4f), -0.5K₂₃[O₂], The oxygen inhibition effect causes a delayed efficacy defined as “induction time”, at that time oxygen is totally depleted, and thus type-I efficacy starts to increase faster. As shown in Figure 4 that large k37 leads to a lower efficacy.

c) In contrast to UVX, a green-light crosslink (GLX) system predominated by an oxygen-mediated type-II process, where the single-monomer radical (R’) induced type-I conversion is not very efficient. Therefore, additive co-initiator (arginine) was proposed by Wertheimer et al [26] for improved efficacy, which was analyzed by Lin [15].

d) For GLX the conversion may be also enhanced by additive monomer (B), as shown by the extra radical term in Eq. (1c), k’(R+S), in which the total rate function given by Eq. (4e) has an enhance factor of [1+ [B]/[A]]^0.5]; which is proportional to the initial concentration ratio [B₀sub>]/[A₀sub>]. In GLX system, in the absence of oxygen and without the enhancer [B] (or S=0), the conversion is contributed from k₇T₁ and k’R, which might not sufficient for effective crosslinking; thus, it requires the extra monomer [B] and its radical S’.

e) For GLX, in the presence of D_2O, which extends the lifetime of singlet oxygen, i.e., a smaller relaxation rate (k₆), thus a larger T₂, based on our Eq. (7b). In contrast, sodium azide which quenches singlet oxygen and other reactive radicals (R and S), i.e., increasing of k₅ and k₆, thus shortening T₁ and T₂, and partially inhibited RB photobleaching, shown by Eq. (6a) with a reduced conversion as measured by Wertheimer et al [26].

f) Our ZC-formula, in Eq. (9) that higher dose (E0) is needed for a deeper ZC. Thus, for a given depth, the enhanced dose factor (EF) of arginine will reduce the required light dose (E₀).

g) This controversial issue of the role of oxygen in UVX and GLX system was explained by Wertheimer et al [26] that O₂ diffused deeper and crosslinking occurs at a greater depth in the tissue, after the crosslinkable sites was reacted. However, our formulas support the kinetic proposed by Lin [11] that type-I and type-II co-exist, initially, and then predominated by type-I after oxygen is depleted.

h) As discussed earlier in (b), oxygen may play an enhancement or inhibition effect for the overall efficacy. This feature may be analyzed by the two-competing components shown by RT in Eq. (4e): the K12[O2] term provides the oxygen-mediated type-II efficacy; whereas the reduction factor of g, (k₃/k₇)[O₂]/[A]+[B] and second term of Eq. (4f), 0.5K₂3[O₂], both cause oxygen inhibition. Therefore, the net effect of oxygen is the balance between these two components.

Efficacy may be improved by additive enhancer-monomer in a 2-monomer system or extended lifetime of photosensitizer tripletstate or oxygen singlet. Higher I0 and radical coupling rate constant (k’) lead to faster depletion of RB and oxygen concentration; and faster transient rising efficacy, but a lower steady-state efficacy. Conversion efficacy is an increasing function of the ratio [B]/[A]. In contrast, efficacy is a decreasing function of the rate ratio of oxygen and triplet state, resulted by the stronger oxygen inhibition. The role of depth (z) plays an opposite trend as that of light intensity, in which RB and oxygen have faster depletion on the stroma surface (z=0) than inside the stroma. Efficacy may be improved by additive enhancer-monomer in a 2-monomer system or extended lifetime of photosensitizer triplet-state or oxygen singlet. Our analytic formulas provide useful guidance for the scaling laws for further clinical studies, in which empirical data will validate the accuracy of the scaling laws.

1. Fouassier JP (1995) Photoinitiation, photo-polymerization, and photocuring: fundamentals and applications. Hanser Gardner Publications, Munich, Germany.
2. Odian G (2006) Principles of Polymerization. (4^th edn), John Wiley & Sons, New York, USA.
3. Chen FM, Shi S (2014) Principles of Tissue Engineering (4^th edn), Elsevier, New York, USA.
4. Wohlers T, Caffrey T (2016) 3D printing and additive manufacturing state of the industry. Annual Worldwide Progress Report. Wohlers Report, Wohlers Associates, USA.
5. Chen FH, Pathreeker S, Saeid B, Hosein ID (2017) Synthesis of micropillar arrays via photopolymerization: an in situ study of light-induced formation, growth kinetics, and the influence of oxygen inhibition. Macromolecules 50(15): 5767-5778.
6. Cabral JT, Hudson SD, Harrison C, Douglas JF (2004) Frontal photopolymerization for microfluidic applications. Langmuir 20(23): 10020-10029.
7. O’Brien AK, Bowman CN (2006) Modeling the effect of oxygen on photopolymerization kinetics. Macromol Theory Simul 15(2): 176-182.
8. Dendukuri D, Panda P, Haghgooie R, Kim JM, Hatton TA, et al. (2008) Modeling of oxygen-inhibited free radical photopolymerization in a PDMS microfluidic device. Macromolecules 41(22): 8547-8556.
9. Cramer NB, O'Brien CP, Bowman CN (2008) Mechanisms, polymerization rate scaling, and oxygen inhibition with an ultra-rapid monovinyl urethane acrylate. Polymer 49(22): 4756-4761.
10. Alvankarian J, Majlis BY (2015) Exploiting the oxygen inhibitory effect on UV curing in microfabrication: a modified lithography technique. PLoS ONE 10(3): e0119658.
11. Lin JT (2018) Efficacy S-formula and kinetics of oxygen-mediated (type-II) and non-oxygen-mediated (type-I) corneal cross-linking. Ophthalmology Research: An international journal 8(1): 1-11.
12. Lin JT, Wang KC (2016) Analytic formulas and numerical simulations for the dynamics of thick and non-uniform polymerization by a UV light. J Polym Res 23: 53.
13. Lin JT, Cheng DC (2017) Modeling the efficacy profiles of UV-light activated corneal collagen crosslinking. PloS ONE 12(4): e0175002.
14. Lin JT, Liu HW, Chen KT, Cheng DC (2019) Modeling the optimal conditions for improved efficacy and crosslink depth of photo-initiated polymerization. Polymers 11(2): E217.
15. Lin JT (2019) Kinetics of enhancement of corneal cross-linking: a proposed model of a two-initiator system. Ophthalmology Research: An International Journal 10(3): 1-6.
16. Cramer NB, Reddy SK, O’Brien AK, Bowman CN (2003) Thiol-ene photopolymerization mechanism and rate limiting step for various vinyl functional group chemistries. Macromolecules 36(21): 7964-7969.
17. Cramer NB, Bowman CN (2013) Thiol-X Click Chemistries in Polymer and Materials Science. In: Lowe AB & Bowman CN (Eds.), RSC Publishing, Cambridge, UK, p. 318.
18. Reddy SK, Cramer NB, Bowman CN (2006) Thiol-Vinyl mechanisms. 2. kinetic modeling of ternary thiol-vinyl photopolymerizations. Macromolecules 39(10): 3681-3687.
19. Okay O, Bowman CN (2005) Kinetic modeling of thiol-ene reactions with both step and chain growth aspects. Macromol Theory Simul 14(4): 267-277.
20. Claudino M, Jonsson M, Johansson M (2013) Thiol-ene coupling kinetics of D-limonene: a versatile ’non-click’ free-radical reaction involving a natural terpene. RSC Adv 3(27): 11021-11034.
21. Li Y, Su H, Feng X, Wang Z, Guo K, et al. (2014) Thiol-Michael “click” chemistry: another efficient tool for head functionalization of giant surfactants. Polym. Chem 5(21): 6151-6162.
22. Wang C, Zhang X, Podgoŕski M, Xi W, Shah P, et al. (2015) Monodispersity/narrow polydispersity cross-linked microparticles prepared by step-growth thiol-michael addition dispersion polymerizations. Macromolecules 48(23): 8461-8470.
23. Zhang X, Xi W, Wang C, Podgoŕski M, Bowman CN (2016) Visible-light-initiated thiol-michael addition polymerizations with coumarin-based photobase generators: another photoclick reaction strategy. ACS Macro Lett 5(2): 229-233.
24. Claudino M, Zhang X, Alim MD, Podgoŕski M, Bowman CN (2016) Mechanistic kinetic modeling of thiol-michael addition photopolymerizations via photocaged “superbase” generators: An Analytical Approach. Macromolecules 49(21): 8061-8074.
25. Huang S, Sinha J, Podgoŕski M, Zhang X, Claudino M, et al. (2018) Mechanistic modeling of the thiol-michael addition polymerization kinetics: structural effects of the thiol and vinyl monomers. Macromolecules 51(5): 5979-5988.
26. Wertheimer CM, Elhardt C, Kaminsky SM, Pham L, Pei Q, et al. (2019) Enhancing rose bengal photosensitized protein crosslinking in the cornea. Invest Ophthalmol Vis Sci 60(6): 1845-1852.