- Submissions

Full Text
Research in Medical & Engineering Sciences
On Problematic Issues of Physical Chemistry
Korablev GA*
Izhevsk State Agricultural Academy, Russia
*Corresponding author: Korablev GA, Izhevsk State Agricultural Academy, Russia
Submission: June 27, 2019;Published: July 09, 2019

ISSN: 2576-8816Volume8 Issue1
Abstract
In systems in which the interaction proceeds along the potential gradient (positive work), the resulting potential energy, as well as the reduced mass, are found based on the principle of adding reciprocals of the corresponding values of subsystems. This is the corpuscular process and the entropy can be its theoretical concept. In the systems in which the interaction proceeds against the potential gradient (negative work), the algebraic addition of their masses, as well as the corresponding energies of subsystems, are performed. This is the wave process and the negentropy can be its theoretical concept. The resonance stationary state of the systems is realized under the condition of equality of degrees of their corpuscular and wave interactions. Such correlations are confirmed by the equations of Plank constant, constant of fine structure and for π. These principles can be practically applied to seek for optimal technological solutions.
Keywords: The first law of thermodynamics; Gradient of the directivity of processes; Wave-particle duality, Entropy, Negentropy
Introduction
In the process of research, not at once but nearly always, you come across the necessity to solve pending problems. Such problematic issues also exist in physical chemistry. Here are some examples. The analysis of kinetics of various physical and chemical processes shows that in some cases the direct addition of velocities, kinetic or energy characteristics is performed, in others-their reciprocals are added. In particular, such supposition is confirmed by the formula of electron transport possibility due to the overlapping of wave functions 1 and 2 (in steady state) during electron-conformation interactions:
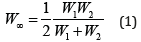
Equation (1) is used when evaluating the characteristics of diffusion processes followed by non-radiating transport of electrons in proteins [1].
And also: “From classical mechanics it is known that the relative motion of two particles with the interaction energy U(r) takes place as the motion of material point with the reduced mass μ:
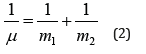
in the field of central force U(r), and general translational motion-as a free motion of material point with the mass:
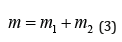
Such things take place in quantum mechanics as well” [2]. At the same time, the problem of quantum-wave dualism is still not completely solved, though the application of de Broglie equation allows defining the manifestation borders of such phenomena. But which property predominates depends on the process conditions. And it is quite complicated to define in advance which part of them will operate in each particular case, although it is known that the wave picture is more often takes place at low energies, and corpuscular-at high ones.
One of the founders of quantum mechanics Max Born said about this: “Each process can be interpreted either from corpuscular or wave point of view. However, the proof that we are really dealing with particles or waves is beyond our capabilities since we are not able to define all characteristic properties of the process. Therefore, we can say that wave and corpuscular descriptions should be considered only as two complementing each other methods of analyzing one and the same objective process” [3]. Therefore, these problematic issues of physical chemistry need to be further investigated and discussed. The multifaceted manifestation of the idea of entropy is of considerable interest. In thermophysical processes entropy (S) is the function of the system state whose differential in the elementary reversible process equals the relation between the infinitely little quantity of heat transferred to the systems and its absolute temperature:
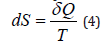
Using such heat-physical definition we can calculate only the difference between entropies. The entropy itself can only be found with the accuracy to the constant summand (integration constant).
In statistic thermodynamics the entropy of the isolated and equilibrious system equals the logarithm of the probability of its definite macrostate:
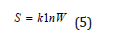
where W-number of available states of the system or degree of the degradation of microstates; k- Boltzmann’s constant.
These correlations are general assertions of macroscopic character, they do not contain any references to the structure elements of the systems considered and they are completely independent from microscopic models [4]. Therefore, the application and consideration of these laws has multifaceted manifestations, which are most fruitfully used in statistic thermodynamics. The notion of entropy, stemming from the second law of thermodynamics, is the criterion of the process directedness and degree of the system randomness. In this investigation the attempt is made to illustrate the above problems from the position of notions of the directedness of such processes.
Gradient of the Directedness of the Processes of Structural Interactions
For moving thermodynamic systems, the first commencement of thermodynamics is as follows:
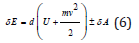
where: amount of energy transferred to the system;
element-characterize the changes in internal and kinetic energies of the system;
-work performed by the system;
-work performed with the system.
As the work value numerically equals the change in the potential energy, then:
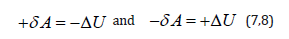
It is probable that not only in thermodynamic but in many other processes in the dynamics of moving particles interaction not only the value of potential energy is critical, but its change as well. Therefore, the following should be fulfilled for two-particle interactions:
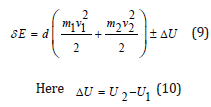
where U2 and U1 and potential energies of the system in final and initial states.
The character of the change in the potential energy value (ΔU) was analyzed by its sign for various potential fields and the results are given in Table 1 [5].
Table 1:
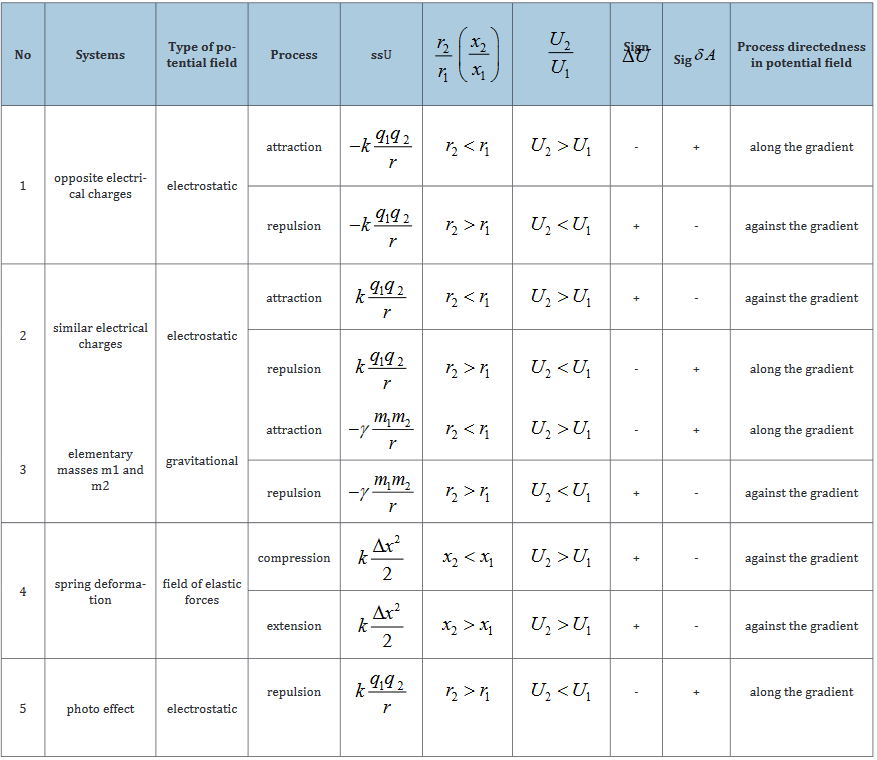
From the table it is seen that the values and accordingly (positive work) correspond to the interactions taking place along the potential gradient, and (negative work) occur during the interactions against the potential gradient.
Thus:
a. In the systems in which the interactions proceed along the potential gradient (positive work) the resulting potential energy is found based on the principle of adding reciprocals of the corresponding energies of subsystems [5]. Similarly, the reduced mass for the relative motion of two-particle system is calculated.
b. In the systems in which the interactions proceed against the potential gradient (negative work) the algebraic addition of their masses as well as the corresponding energies of subsystems is performed (by the analogy with Hamiltonian).
Corpuscular Wave Dualism
The solution of Lagrangian equation thought he reduced mass for the relative motion of isolated system of two interacting material points can be as follows [5]:

where ΔU1 and ΔU2-potential energies of material points on the elementary area of interactions, ΔU- resulting (mutual) potential energy of these interactions.
The formalism of equations (1,11) is not principally new. The following equation was obtained by Compton effect in 1924 already:
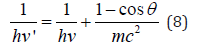
Here: hν›-dissipated photon energy, hν-falling photon energy, mc2-electron own energy, ϴ-dissipation angle. At the same time, the energy of photons decreases by the value additionally obtained by the electron. The act of quantum action takes place in this way, the result of which is the energy redistribution between corpuscular and wave parameters of interacting systems.
In equation (12) for corpuscular process the principle of reverse addition indicates that the process flows along the potential gradient. Similar phenomenon is confirmed by the well-known Einstein’s equation by photo effect, where the value of the work of electron output is positive. In atom during the electron-atom interaction the reduced mass (and also the corresponding energy) is calculated by the principle of reverse addition [6]. This is the corpuscular process, which proceeds along the potential gradient. And irradiation during quantum transitions is already the wave process flowing against the potential gradient.
Electric current is the motion of electrons along the potential gradient. If we assume that the magnetic field created by it is a wave process, there should be the correlation between electric and magnetic constants. The difference between phases of electric and magnetic oscillations is π/2 .
Entering coefficient (2/π)2 we have the equation for Planck’s constant with the accuracy close to the one of the initial data.
Here а = 0.0023293-experimental quantum correction to spine gs-electron factor, ɛ-electric constant, μ- magnetic constant, h-Planck’s constant. For a free electron Pе=Wr, where W=0.510034 МeV=0.81872˟10-13J. The value of classical electron radius r = 2.81794˟10-15m was used as a dimensional characteristic and, therefore, Ре=2.30712˟10-28Jm.

The proportionality coefficient in equation (13) has the velocity dimensionality (m/sec) for the correlation (F/Hn), i.e. in such a way the velocity of redistributions of energy in the system “particle-wave” is characterized. Summing up the formalism of equations (1,11,12) on all the other interactions proceeding along the potential gradient, it can be concluded that in these cases corpuscular interactions proceed, but the wave dualism corresponds to the interactions against the potential gradient.
Entropy in Corpuscular-Wave Interactions
Figure 1:Nomogram of the dependence of the degree of structural interactions (ρ) on coefficient α.
The graphic change in the degree of structural interactions (ρ), depending on the relative difference of energy parameters of the structures (coefficient α), is characterized [5] by nomogram 1 (Figure 1). In the given approach this nomogram is identical to the dynamics of entropic changes in the systems and its ambidexteral variant (nomogram 2 is not given) characterizes negentropic dynamics. Many phenomena and processes in nature, engineering and even in economy are described by similar S-curves [7-12], which were called “Lines of Life”. In thermodynamics reversible and irreversible processes are distinguished. Thus, in irreversible expansion the gas transits from less probable to more probable state, i.e. this process flows along the probability gradient. Similarly, the transit of heat from a hotter body to a colder one is irreversible, which also flows along the temperature gradient. As it was already demonstrated, corpuscular interactions also flow along the field gradient. Therefore, it is presumed that the entropy can be a theoretical concept of corpuscular processes. In the open system there is an interaction with the external environment and general change of the entropy (ds) is expressed by the equation:
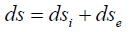
Here dsi -changes of the entropy as a result of the processes inside the system (nomogram 1), dse - changes of negentropy conditioned by the interaction with the environment (nomogram 2). Then within the time dt:
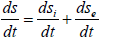
where ds/dt -total velocity of the entropy change in the closed system,dsi/dt-entropy products,dse/dt-entropy flow (negentropy).
For the dynamic stationary state, the total velocity of entropy change must equal zero: ds/dt=0.
And then
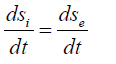
Thus, the entropy products in the stationary state are completely compensated by the negentropy flow. The processes flowing in an open system are reversible. For example, all mechanical processes without friction belong to them. But there is friction in actual processes, as well as the conversion of mechanical work into heat, and this is already an irreversible process [13].
In the thermal machine there is heat conversion from a colder body to a hotter one. In this case and in all reversible processes the work is performed against the field gradient. And the entropy corresponding to these processes is called negentropy (negative entropy). As it was demonstrated, the system work against the field gradient corresponds to the wave processes, e.g., in electric field generator.
Such analogy in directed entropic and corpuscular-wave processes allows assuming that the entropy is a theoretical concept of corpuscular interactions, and negentropy-a concept of wave interactions. Besides, this analogy gives the possibility to use the entropic equation of the stationary state of open systems for the corresponding corpuscular-wave processes. At the same time, the following correlation is fulfilled in the thermal machine: “During the circular process the increase in the system entropy due to the incoming heat is completely compensated by the decrease in entropy due to the heat output, and the total entropy value equals zero” [14]:
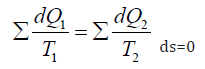
As applicable to corpuscular-wave processes, the condition of dynamic stationary state is the condition of equilibrium of their degrees of structural interactions:

This condition is graphically fulfilled when nomogram 1 (entropy) is overlapping nomogram 2 (negentropy), which gives the following value:
ρ=50%
The stationary state is mathematically and graphically (by nomogram) fulfilled by the equation:
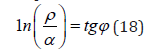
Where φ= 54°44ˈ-geodesic angle.
Thus, e.g., for the constant fine structure this equation is as follows:
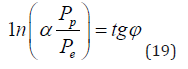
Here:Pp = WpR =938.2756 МeV х 0.856 fm = 803.107 МeVfm
Pe=Wer =1.43998 МeVfm
α- fine structure constant
Pp and Pe-energy parameters of free proton and electron
Wp and We - their energy masses
R-dimensional characteristic of proton [15]
r-classical radius of electron.
Similarly, for the equation for π:
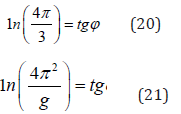
Thus, the equality of corpuscular and wave interactions defines the resonance stationary sate of the system. This condition corresponds to the most optimal technological variants and is widely revealed in nature, as well as in fractal systems. The fractal structures are formed under the condition of equilibrium statistic interaction of entropic and negentropic characteristics of all particles. Based on the equations:

In macroworld such principle is fulfilled not only for Koch snowflakes but also in many other natural phenomena, e.g., during the formation of clouds and even during dust concentration in premises.
Conclusion
1. In systems in which the interaction proceeds along the potential gradient (positive work), the resulting potential energy, as well as the reduced mass, are found based on the principle of adding reciprocals of the corresponding values of subsystems. This is the corpuscular process and the entropy can be its theoretical concept.
2. In the systems in which the interaction proceeds against the potential gradient (negative work), the algebraic addition of their masses, as well as the corresponding energies of subsystems, are performed. This is the wave process and the negentropy can be its theoretical concept.
3. The resonance stationary state of structural processes takes place under the condition of equality of the degrees of corpuscular and wave interactions.
4. These correlations are confirmed by the equations of Planck’s constant, fine structure constant and for π.
These principles can be practically applied to seek for optimal technological solutions.
References
- Rubin AB (1987) Theoretical biophysics. М Vysshaya Shkola, USA, pp. 319.
- Blokhintsev DI (1961) Basics of quantum mechanics. М Vysshaya Shkola, USA, pp. 512.
- Marison JB (1986) General physics with biological examples. М Vysshaya shkola, USA, pp. 623.
- Gribov LA, Prokofyeva NI (1992) Basics of physics. М Vysshaya Shkola, USA, pp. 430.
- Korablev GA (2018) Spatial-energy interactions. Stary Oskol, USA, pp. 132.
- Eyring G, Walter J, Kimball G (1948) Quantum chemistry, USA, pp. 528.
- Korablev GA, Zaikov GE (2012) Bio-structural energy criteria of functional states in norm and pathology. Applied Chemistry and Biotechnology 1(2): 118-124.
- Korablev GA, Petrova NG, Kodolov VI, Korablev RG, Zaikov GE, et al. (2014) Nomograms of biophysical and economic processes. Applied Chemistry and Biotechnology 2(7): 48-57.
- Korablev GA, Zaikov GE, Khokhriakov NV (2013) Calculation of bond in cluster aqueous nanostructures. Journal of Characterization and Development of Novel Materials 5(3): 213-218.
- Korablev GA, Zaikov GE (2013) Energy correlations of the affinity to the electron with the values of spatial-energy parameter. Chemical Physics and Mesoscopy 15(3): 447-456.
- Korablev GA, Zaikov GE (2014) Spatial-energy characteristics of photosynthesis. Applied Chemistry and Biotechnology 3(8): 53-66.
- Korablev GA, Petrova NG, Osipov AK, Zaikov GE (2013) Diversified demonstration of entropy. Nanotechnologies to Nanoindustry, USA, pp. 120-130.
- Chulanovskaya MV (1972) Course of physics for biologists. Leningrad University, Russia, pp. 248.
- Gevorkyan RG, Shepel VV (1972) Course of general physics. М Vysshaya shkola, USA, pp. 600.
- Murodyan RM (1977) Physical and astrophysical constants and their dimensional and dimensionless combinations. FEChAYa М Atomizdat 8(1): 175-192.
© 2019 Korablev GA. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






