Transformation of High-Energy Bonds in ATP

During the interaction of oppositely charged heterogeneous systems the certain compensation of volume energy of interacting structures takes place which leads to the decrease in the resulting energy (for example, during the hybridization of atomic orbitals). But this is not the direct algebraic deduction of the corresponding energies. The comparison of multiple regularities of physical, chemical and biological processes allows assuming that in such and similar cases the principle of adding the reciprocals of volume energies or kinetic parameters of interacting structures is executed.

Lagrangian equation for the relative movement of the system of two interacting material points with the masses m₁ и m ₂ in coordinate х is as follows:

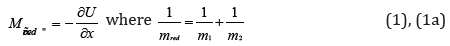
here U-mutual potential energy of material points; m_red-reduced mass. Herein х”=а (system acceleration).

For the elementary areas of interactions Δх we can accept:

Then: mred аΔх = -ΔU;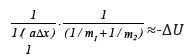 or: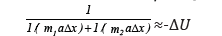

Since the product miaΔx by its physical sense equals the potential energy of each material point (-ΔU_i), then:

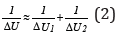
Thus, the resulting energy characteristic of the system of two interacting material points is found by the principle of adding the reciprocals of initial energies of interacting subsystems. “The electron with the mass m moving about the proton with the mass М is equivalent to the particle with the mass: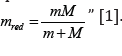

Therefore, modifying the equation (2) we can assume that the energy of atom valence orbitals (responsible for interatomic interactions) can be calculated [2] by the principle of adding the reciprocals of some initial energy components based on the equations:

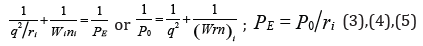
here: Wi-orbital energy of electrons [3];

ri - orbital radius of i orbital [4];

q=Z*/n* -by [5,6],

ni - number of electrons of the given orbital,

Z* and n*- nucleus effective charge and effective main quantum number, r-bond dimensional characteristics.

The value РО is called a spatial-energy parameter (SEP), and the value Р_E -effective Р-parameter (effective SEP). Effective SEP has a physical sense of some averaged energy of valence orbitals in the atom and is measured in energy units, e.g. in electron-volts (eV).

The values of Р0-parameter are tabulated constants for electrons of the given atom orbital.

For SEP dimensionality:

where [E], [h] and [υ]-dimensionalities of energy, Planck’s constant and velocity.

The introduction of P-parameter should be considered as further development of quasi-classical concepts with quantummechanical data on atom structure to obtain the criteria of phaseformation energy conditions. For the systems of similarly charged (e.g. orbitals in the given atom) homogeneous systems the principle of algebraic addition of such parameters is preserved

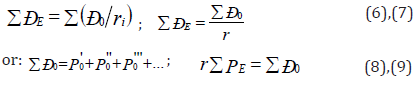
Here P-parameters are summed up by all atom valence orbitals.

To calculate the values of Р_E-parameter at the given distance from the nucleus either the atomic radius (R) or ionic radius (rI) can be used instead of r depending on the bond type. Let us briefly explain the reliability of such an approach. As the calculations demonstrated the values of Р_E-parameters equal numerically (in the range of 2%) the total energy of valence electrons (U) by the atom statistic model. Using the known correlation between the electron density (β) and intra-atomic potential by the atom statistic model [7], we can obtain the direct dependence of Р_E-parameter on the electron density at the distance ri from the nucleus. The rationality of such technique was proved by the calculation of electron density using wave functions by Clementi [8] and comparing it with the value of electron density calculated through the value of Р_E- parameter.

The modules of maximum values of the radial part of Ψ-function were correlated with the values of Р0-parameter and the linear dependence between these values was found. Using some properties of wave function as applicable to P-parameter, the wave equation of P-parameter with the formal analogy with the equation of Ψ-function was obtained [9].

Wave Properties of P-Parameters and Principles of their Addition

Since Р-parameter has wave properties (similar to Ψ’-function), the regularities of the interference of the corresponding waves should be mainly fulfilled at structural interactions. The interference minimum, weakening of oscillations (in antiphase) occurs if the difference of wave moves (Δ) equals the odd number of semi-waves:

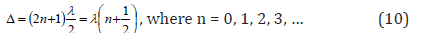
As applicable to P-parameters this rule means that the interaction minimum occurs if Р-parameters of interacting structures are also “in antiphase” either oppositely charged or heterogeneous atoms (for example, during the formation of valence-active radicals CH, CH2, CH3, NO2 …,etc.) are interacting.

In this case P-parameters are summed by the principle of adding the reciprocals of P-parameters equations (3,4). The difference of wave move (Δ) for P-parameters can be evaluated via their relative value (γ=Ð₂/Ð₁) of relative difference of P-parameters (coefficient α) which at the interaction minimum produce an odd number: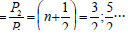When n = 0 (main state) Ð₂/Ð₁=1/2(11)

It should be pointed out that for stationary levels of onedimensional harmonic oscillator the energy of these levels ( 1) 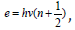, therefore in quantum oscillator, in contrast to the classical one, the least possible energy value does not equal zero. In this model the interaction minimum does not provide zero energy corresponding to the principle of adding reciprocals of P-parameters equations (3,4). The interference maximum, strengthening of oscillations (in phase) occurs if the difference of wave move equals the even number of semi-waves:

And then:

By the analogy, for “degenerated” systems (with similar values of functions) of two-dimensional harmonic oscillator the energy of stationary states:

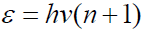
By this model the interaction maximum corresponds to the principle of algebraic addition of P-parameters equations (6-8). When n=0 (main state) we have Р2=Р¹, or: the interaction maximum of structures occurs if their P-parameters are equal. This concept was used [2] as the main condition for isomorphic replacements and formation of stable systems.

During the formation of solid solutions and in other structural equilibrium-exchange interactions the unified electron density should be established in the contact spots between atomscomponents. This process is accompanied by the re-distribution of electron density between valence areas of both particles and transition of a part of electrons from some external spheres into the neighboring ones. It is obvious that with the proximity of electron densities in free atoms-components the transition processes between the boundary atoms of particles will be minimal thus contributing to the formation of a new structure. Thus, the task of evaluating the degree of such structural interactions in many cases comes down to comparative assessment of electron density of valence electrons in free atoms (on the averaged orbitals) participating in the process. Therefore, the maximum total solubility evaluated via the structural interaction coefficient α is defined by the condition of minimal value of coefficient α which represents the relative difference of effective energies of external orbitals of interacting subsystems:

where РS - structural parameter is found by the equation:

here N1 and N2 - number of homogeneous atoms in subsystems.

The nomogram of the dependence of structural interaction degree (ρ) upon the coefficient α, the same for the wide range of structures, was prepared by the data obtained. Isomorphism as The nomogram of the dependence of structural interaction degree (ρ) upon the coefficient α, the same for the wide range of structures, was prepared by the data obtained. Isomorphism as a phenomenon is usually considered as applicable to crystalline structures. But obviously the similar processes can also take place between molecular compounds where the bond energies can be accessed via the relative difference of electron densities of valence orbitals of interacting atoms. Therefore, the molecular electronegativity is rather easily calculated via the values of corresponding P-parameters. In complex organic structures the main role in intermolecular and intramolecular interactions can be played by separate “blocks” or fragments considered as “active” areas of the structures. Therefore, it is necessary to identify these fragments and evaluate their spatial-energy parameters. Based on wave properties of P-parameter, the total P-parameter of each element should be found following the principle of adding the reciprocals of initial P-parameters of all the atoms. The resulting P-parameter of the fragment block or all the structure is calculated following the rule of algebraic addition of P-parameters of their constituent fragments. Apparently, spatial-energy exchange interactions (SEI) based on leveling the electron densities of valence orbitals of atoms-components have in nature the same universal value as purely electrostatic coulomb interactions and complement each other. Isomorphism known from the time of E. Mitscherlich (1820) and D.I. Mendeleev (1856) is only a special demonstration of this general natural phenomenon.

The quantitative side of evaluating the isomorphic replacements both in complex and simple systems rationally fits into P-parameter methodology. More complicated is the problem of evaluating the degree of structural SEI for molecular structures, including organic ones. Such structures and their fragments are often not completely isomorphic to each other. Nevertheless, SEI is going on between them and its degree can be evaluated either semi-quantitatively numerically or qualitatively. By the degree of isomorphic similarity all the systems can be divided into three types:

I. Systems mainly isomorphic to each other-systems with approximately the same number of heterogeneous atoms and cumulatively similar geometric shapes of interacting orbitals.

II. Systems with organic isomorphic similarity-systems which:

1. Either differ by the number of heterogeneous atoms but have cumulatively similar geometric shapes of interacting orbitals.

2. Or have certain differences in the geometric shape of orbitals but have the same number of interacting heterogeneous atoms.

III. Systems without isomorphic similarity-systems considerably different both by the number of heterogeneous atoms and geometric shape of their orbitals.

Taking into account the experimental data, all SEI types can be approximately classified as follows:

Systems I

1. α<(0-6)%; ρ = 100%. Complete isomorphism, there is complete isomorphic replacement of atoms-components;

2. 6 % <α <(25-30)%; ρ=98-(0-3)%. There is wide or unlimited isomorphism.

3. α>(25-30)%; no SEI.

Systems II

1. α<(0-6)%;

a. There is reconstruction of chemical bonds that can be accompanied by the formation of a new compound.

b. Cleavage of chemical bonds can be accompanied by a fragment separation from the initial structure but without adjoining and replacements.

2. 6%<α<(25-30)%; the limited internal reconstruction of chemical bonds is possible but without the formation of a new compound and replacements.

3. α>(20-30)%; no SEI

Systems III

1) α<(0-6)%

a. The limited change in the type of chemical bonds in the given fragment is possible, there is an internal re-grouping of atoms without the cleavage from the main molecule part and replacements.

b. The change in some dimensional characteristics of the bond is possible.

2) 6%<α<(25-30)%

A very limited internal re-grouping of atoms is possible.

3) α>(25-30)%; no SEI.

When considering the above systems, it should be pointed out that they can be found in all cellular and tissue structures in some form but are not isolated and are found in spatial-time combinations. The values of α and ρ calculated in such a way refer to a definite interaction type whose nomogram can be specified by fixed points of reference systems. If we take into account the universality of spatial-energy interactions in nature, such evaluation can have the significant meaning for the analysis of structural shifts in complex bio-physical and chemical processes of biological systems.

Fermentative systems contribute a lot to the correlation of structural interaction degree. In this model the ferment role comes to the fact that active parts of its structure (fragments, atoms, ions) have such a value of Р_E-parameter which equals the Р_E-parameter of the reaction final product.

That is the ferment is structurally “tuned” via SEI to obtain the reaction final product, but it will not enter it due to the imperfect isomorphism of its structure (in accordance with III). The important characteristics of atom-structural interactions (mutual solubility of components, chemical bond energy, energy of free radicals, etc) for many systems were evaluated following this technique [10,11].

Based on the equations (3-5) with the initial data calculated by quantum-mechanical methods [3-6] we calculate the values of Р0- parameters for the majority of elements being tabulated, constant values for each atom valence orbital. Mainly covalent radii by the main type of the chemical bond of interaction considered were used as a dimensional characteristic for calculating Р_E-parameter (Table 1). The value of Bohr radius and the value of atomic (“metal”) radius were also used for hydrogen atom.

Table 1: Р-parameters of atoms calculated via the bond energy of electrons.

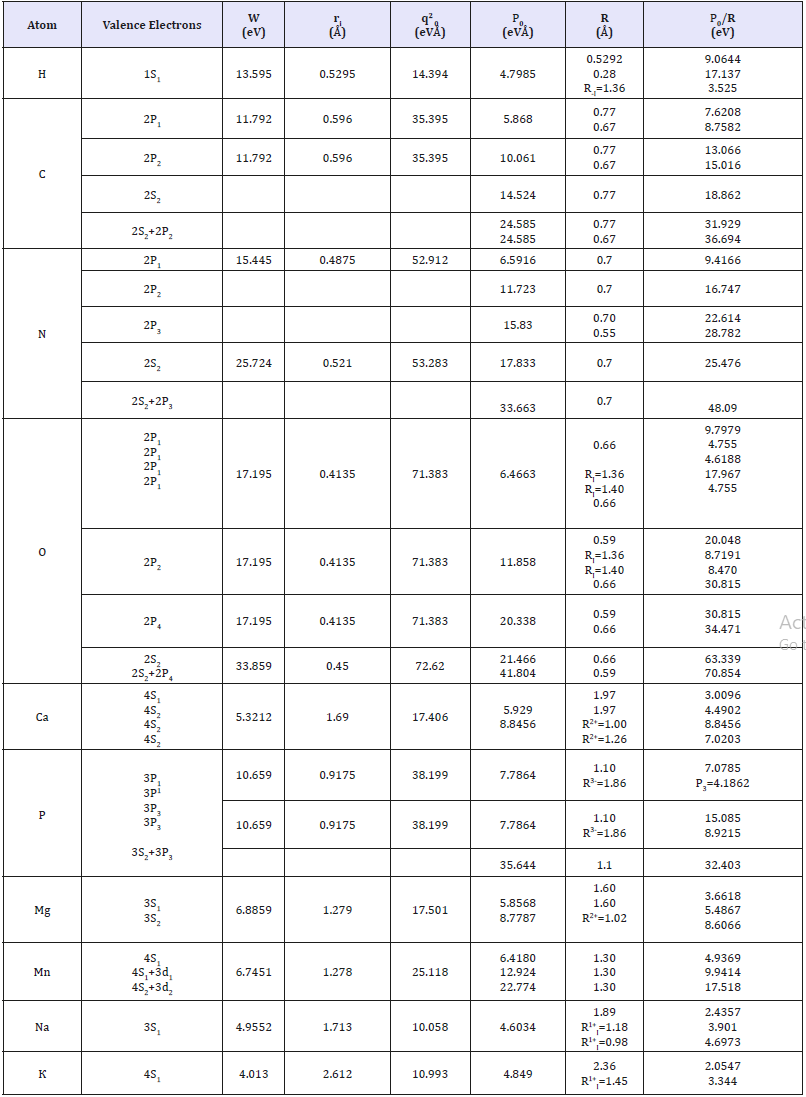
Table 2:Structural РS-parameters calculated via the bond energy of electrons.

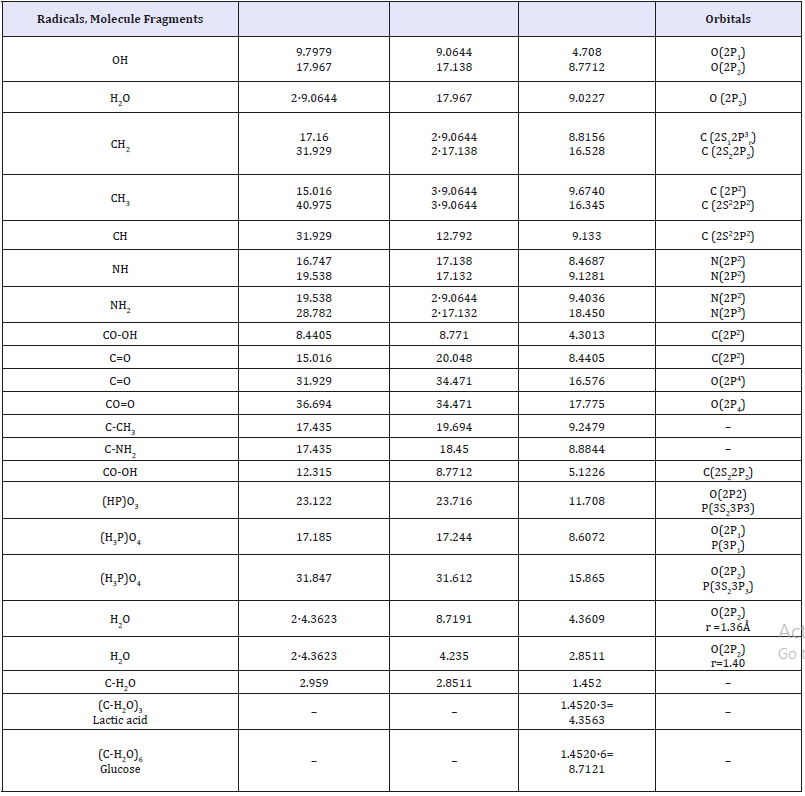
In some cases, the bond repetition factor for carbon and oxygen atoms was taken into consideration [10]. For a number of elements, the values of Р_E-parameters were calculated using the ionic radii whose values are indicated in column 7. All the values of atomic, covalent and ionic radii were mainly taken by Belov-Bokiy, and crystalline ionic radii by Batsanov [12]. The results of calculating structural РS-parameters of free radicals by the equation (15) are given in Table 2. The calculations are done for the radicals contained in protein and amino acid molecules (СН, СН₂, СН₃, NH₂ etc), as well as for some free radicals formed in the process of radiolysis and dissociation of water molecules.

The technique previously tested [10] on 68 binary and more complex compounds was applied to calculate the energy of coupled bond of molecules by the equations:

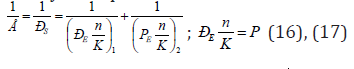
where n-bond average repetition factor, К-hybridization coefficient which usually equals the number of registered atom valence electrons. Here the P-parameter of energy characteristic of the given component structural interaction in the process of binary bond formation. “Non-valence, non-chemical weak forces act … inside biological molecules and between them apart from strong interactions” [13]. At the same time, the orientation, induction and dispersion interactions are used to be called Van der Waals. For three main biological atoms (nitrogen, phosphorus and oxygen) Van der Waals radii numerically equal approximately the corresponding ionic radii (Table 3). It is known that one of the reasons of relative instability of phosphorus anhydrite bonds in ATP is the strong repulsion of negatively charged oxygen atoms. Therefore, it is advisable to use the values of Р-parameters calculated via Van der Waals radii as the energy characteristic of weak structural interactions of biomolecules (Table 3).

Table 3:Ionic and Van der Waals radii (Å).

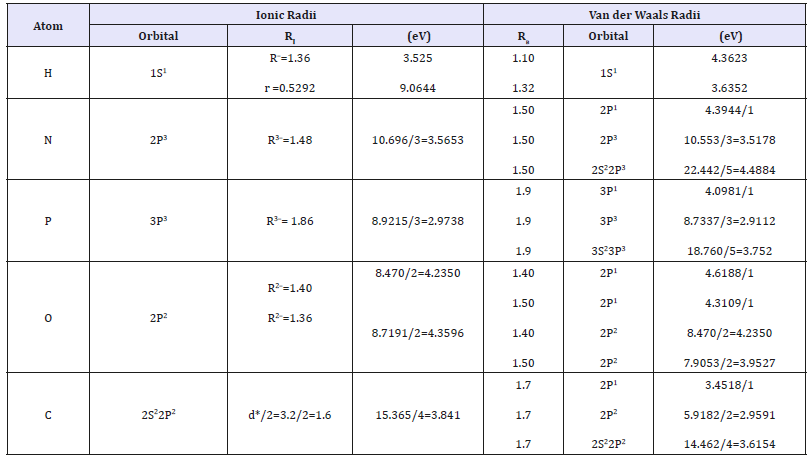
d*-contact distance between С-С atoms in polypeptide chains [13].

Bond energies for Р and О atoms were calculated taking into account Van der Waals distances for atomic orbitals: ЗР¹ (phosphorus)-2Р¹ (oxygen) and for ЗР³ (phosphorus)-2Р2 (oxygen). The values of Е obtained slightly exceeded the experimental, reference ones (Table 4). But for the actual energy physiological processes, e.g. during photosynthesis, the efficiency is below the theoretical one, being about 83%, in some cases [14,15]. Perhaps the electrostatic component of resulting interactions at anionanionic distances is considered in such a way. Actually the calculated value of 0.83Е practically corresponds to the experimental values of bond energy during the phospholyration and free energy of ATP in chloroplasts.

Table 4 contains the calculations of bond energy following the same technique but for stronger interactions at covalent distances of atoms for the free molecule Р-О (sesquialteral bond) and for the molecule Р=О (double bond). The sesquialteral bond was evaluated by introducing the coefficient n=1.5 with the average value of oxygen Р_E-parameter for single and double bonds. The average breaking energy of the corresponding chemical bonds in ATP molecule obtained in the frameworks of semi-empirical method PM3 with the help of software GAMESS [16] are given in column 11 of Table 4 for comparison. The calculation technique is detailed in [17]. The calculated values of bond energies in the system К-С-N being close to the values of high-energy bond Р~О in ATP demonstrate that such structure can prevent the ATP synthesis. When evaluating the possibility of hydrogen bond formation, we take into account such value of n K in which К=1, and the value n=3.525/17.037 characterizes the change in the bond repetition factor when transiting from the covalent bond to the ionic one.

Table 4:Bond energy (eV)

At equilibrium-exchange spatial-energy interactions similar to isomorphism the electrically neutral components do not repulse but approach each other and form a new composition whose α in the equations (13,14). This is the first stage of stable system formation by the given interaction type which is carried out under the condition of approximate equality of component P-parameters:

P₁ ≈ P₂

Hydrogen atom, element No 1 with the orbital 1S1 determines the main criteria of possible structural interactions. Four main values of its P-parameters can be taken from Table 1 & 3: for strong interactions: Ð_E′′ =9.0644eV with the orbital radius 0.5292Å and Ð_E′′′ =17.137eV with the covalent radius 0.28Å. For weaker interactions: E Ð′ =4.3623eV and Р_E=3.6352eV with Van der Waals radii 1.10Å and 1.32Å. The values of P-parameters P′ : P′′ : P′′′ relates as 1:2:4. In accordance with the concepts in Section 2, such values of interaction P-parameters define the normative functional states of biosystems, and the intermediary can produce pathologic formations by their values.

Table 5:Bio-structural spatial-energy parameters (eV).

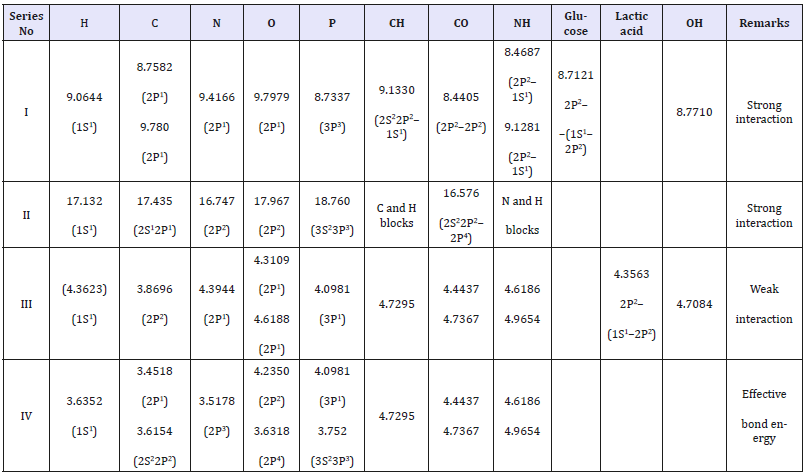
The series with approximately similar values of P-parameters of atoms or radicals can be extracted from the large pool of possible combinations of structural interactions (Table 5). The deviations from the initial, primary values of P-parameters of hydrogen atom are in the range ±7%. The values of P-parameters of atoms and radicals given in the Table define their approximate equality in the directions of interatomic bonds in polypeptide, polymeric and other multi-atom biological systems.

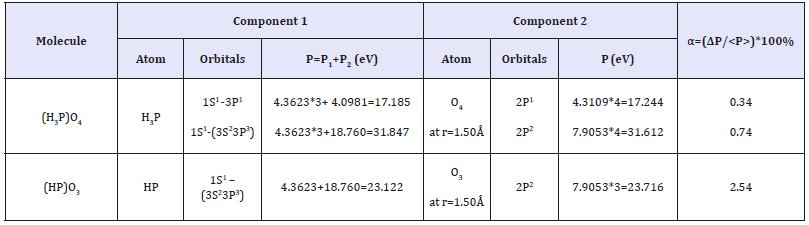
In ATP molecule these are phosphorus, oxygen and carbon atoms, polypeptide chains СО, NH and CH radicals. In Table 5 you can also see the additional calculation of their bond energy taking into account the sesquialteral bond repetition factor in radicals С-О и N-H. On the example of phosphorus acids, it can be demonstrated that this approach is not in contradiction with the method of valence bonds which explains the formation peculiarities of ordinary chemical compounds. It is demonstrated in Table 6 that this electrostatic equilibrium between the oppositely charged components of these acids can correspond to the structural interaction for Н3РО4 3Р¹ orbitals of phosphorus and 2Р¹ of oxygen, and for НРО₃ 3S23Р³ orbitals of phosphorus and 2Р2 of oxygen. Here it is stated that P-parameters for phosphorus and hydrogen subsystems are added algebraically.

Table 6:Structural interactions in phosphorus acids.

It is also known that the ionized phosphate groups are transferred in the process of ATP formation that is apparently defined for phosphorus atoms by the transition from valence-active 3Р¹ orbitals to 3S23Р³ ones, i.e. 4 additional electrons will become valence-active. According to the experimental data the synthesis of one ATP molecule is connected with the transition of four protons and when the fourth proton is being transited the energy accumulated by the ferment reaches its threshold [18,19]. It can be assumed that such proton transitions in ferments initiate similar changes in valence-active states in the system Р-О. In the process of oxidating phospholyration the transporting ATP-synthase uses the energy of gradient potential due to 2Н+ -protons which, in the given model for such a process, corresponds to the initiation of valenceactive transitions of phosphorus atoms from 3Р¹ t o 3 Р³-state. In accordance with the equation (17) we can assume that in stable molecular structures the condition of the equality of corresponding effective interaction energies of the components by the couple bond line is fulfilled by the following equations:

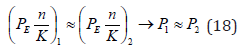
And for heterogeneous atoms (when 1 2 n = n ):

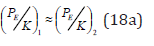
In phosphate groups of ATP molecule, the bond main line comprises phosphorus and oxygen molecules. The effective energies of these atoms by the bond line calculated by the equation (18) are given in Table 4 & 5, from which it is seen that the best equality of Р¹ and Р2 parameters is fulfilled for the interactions Р(3Р³) -8.7337eV and О(2Р2)-8.470eV that is defined by the transition from the covalent bond to Van der Waals ones in these structures. The resulting bond energy of the system Р-О for such valence orbitals and the weakest interactions (maximum values of coefficient К) is 0.781eV (Table 4). Similar calculations for the interactions Р(2Р¹)- 4.0981eV and О(2Р¹)- 4.6188eV produce the resulting bond energy 0.397eV. The difference in these values of bond energies is defined by different functional states of phosphorous acids НРО₃ and Н3РО4 in glycolysis processes and equals 0.384eV that is close to the phosphorylation value (0.34-0.35eV) obtained experimentally. Such ATP synthesis is carried out in anaerobic conditions and is based on the transfer of phosphate residues onto ATP via the metabolite. For example: ATP formation from creatine phosphate is accompanied by the transition of its NH group at ADP to NH2 group of creatine at ATP.

From Table 4 it is seen that the change in the bond energy of these two main radicals of metabolite is 5.3238-4.9654=0.3584eV -taking the equilateral bond N-H into account (as in polypeptides) and 5.3238-4.6186=0.7052eV -for the single bond N-H. This is one of the intermediary results of the high-energy bond transformation process in ATP through the metabolite. From Table 4 & 6 we can conclude that the phosphorous acid Н3РО4 can have two stationary valence-active states during the interactions in the system Р-О for the orbitals with the values of P-parameters of weak and strong interactions, respectively. This defines the possibility for the glycolysis process to flow in two stages. At the first stage, the glucose and Н3РО4 molecules approach each other due to similar values of their P-parameters of strong interactions (Table 2). At the second stage, Н3РО4 P-parameter in weak interactions 4.8779eV (Table 4) in the presence of ferments provokes the bond (Н2О- С)-(С-Н2О) breakage in the glucose molecule with the formation of two molecules of lactic acid whose P-parameters are equal by 4.3563eV. The energy of this bond breakage process equalled to 0.726eV (Table 4) is realized as the energy of high-energy bond it ATP. According to the reference data about 40% of the glycolysis total energy, i.e. about 0.83eV, remains in ATP.

By the hydrolysis reaction in ATP in the presence of ferments 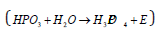for structural РS-parameters (Table 2) Е=11.708+4.3609-15.865=0.276eV.

It is known that the change in the free energy (ΔG) of hydrolysis of phosphorous anhydrite bond of ATP at рН=7 under standard conditions is 0.311-0.363eV. But in the cell the ΔG value can be much higher as the ATP and АDP concentration in it is lower than under standard conditions. Besides, the ΔG value is influenced by the concentration of magnesium ions which is the acting coferment in the complex with ATP. Actually Мg2+ ion has the Р_E- parameter equalled to 8.6066eV (Table 1) which is very similar to the corresponding values of Р-parameters of phosphorous and oxygen atoms. The quantitative evaluation of this factor requires additional calculations.

1. Bond energies of some biostructures have been calculated following P-parameter and quantum-mechanical techniques.

2. High-energy bonds in ATP are formed in the system Р-О under functional transitions of their valence-active states.

The data obtained agree with the experimental ones.

1. Alvir J, Lieberman J, Safferman A, Schwimmer J, Schaaf J (1993) Clozapine-induced agranulocytosis. Incidence and risk factors in the united states. New England Journal of Medicine 329(3): 162-167.
2. En.wikipedia.org. (2019) Neuroleptic malignant syndrome.
3. Europepmc.org. (2019).
4. Pope HG, Cole JO, Choras PT, Fulwiler CE (2019) Apparent neuroleptic malignant syndrome with clozapine and lithium. J Nerv Ment Dis 174(8): 493-495.
5. WikiGenes (2019) WikiGenes-Collaborative Publishing, USA.
6. Kim DC (2012) Maliganant hyperthermia. Korean J Anesthesiol 63(5): 391-401.
7. En.wikipedia.org. (2019) Malignant hyperthermia.
8. Moßhammer D, Schaeffeler E, Schwab M, Mörike K (2014) Mechanisms and assessment of statin-related muscular adverse effects. Br J Clin Pharmacol 78(3): 454-466.
9. Tomaszewski M, Stępień KM, Tomaszewska J, Czuczwar SJ (2019) Statininduced myopathies. Pharmacol Rep 63(4): 859-866.
10. MSD Manual Professional Edition (2019) Malignant hyperthermiainjuries poisoning. MSD Manual Professional Edition, USA.
11. Legge SE, Hamshere ML, Ripke S, Pardinas AF, Goldstein JI, et al. (2016) Genome-wide common and rare variant analysis provides novel & insights in to clozapine-associated neutropenia. Mol Psychiatry 22(10): 1502-1508.
12. SEARCH Collaborative Group, Link E, Parish S, Armitage J, Bowman L, et al. (2019) SLCO1B1 Variants and statin-induced myopathy-a genomewide study. N Engl J Med 359(8): 789-799.
13. Mei Y, Wang SY, Li Y, Yi SQ, Wang CY, et al. (2014) Role of SLCO1B1, ABCB1, and CHRNA1 gene polymorphism on efficacy of rocuronium in Chinese patients. J Clin Pharmacol 55(3): 261-268.
14. En.wikipedia.org. (2019) Genome-wide association study.