Pathological Gait Classification and Segmentation by Processing the Hip Joints Motion Data to Support Mobile Gait Rehabilitation

Gait analysis has by far received the most study as compared to other human body movement [1] because of its readily observable features. Gait comprises a periodic phenomenon in both legs in such a way that the entire body moves from one place to another [2]. A single gait cycle consists of one stride length which is further divided into stance and swing phases. In the stance phase, one leg bears the weight of the body whereas the swing phase causes the leg’s forward motion to propel the body. The swing and stance phases are classified by a cut-off point such that the interval between the toe-off point and heel- strike for a foot represents the swing phase while the stance occurs between the heel-strike and toe-off. Swing and stancephases are further divided into seven sub-phases that include, Initial Contact (IC), Load Response (LR), Mid Stance (MSt), Terminal Stance (TSt), Pre-Swing (PSw), Initial Swing (ISw), Mid- Swing (MSw), and Terminal Swing (TSw) [2,3]. Since a measurement of the gait with foot switches, gyroscopes, and accelerometers can only detect events that are caused by repetitive patterns in the movement and in measured signals, the phases detected from sensors differ from those based on functional tasks. Literature contains a variety of gait segmentation models consisting of a different number of sub-phases varying from two to seven depending upon different clinical aims [4].

An accurate detection of the gait sub-phases is fundamental in clinical gait analysis to interpret kinetic and kinematic data [2]. Correct segmentation of the gait sub-phases can be considered as research initiatives for several scientific studies that include daily life activities classification, assessment of gait anomaly level in patients after interventions or rehabilitation treatments, the synergistic control of robotic devices for the recovery of lower limb mobility, athlete coaching, and distinguishing between normal and pathological gait [4]. Human locomotors system functionality can be affected by various causes leading to atypical gait generation. As an example, a gait cycle usually starts with the forefoot contact instead of a heel strike for patients with an equinus foot. Similarly, a foot-drop may be seen during the swing phase [5] in the case of different neurological and degenerative diseases such as muscular dystrophy, multiple sclerosis, stroke, and Parkinson’s disease. Analysis of the gait biomechanics to a sub-phase level is very useful for a patient’s degree of performance, gait rehabilitation, walking pattern recognition, and other related research [1]. A typical example would include pathological gait which can be diagnosed and evaluated after rehabilitation using different gait features such as stride width, walking speed, cadence, and walking symmetry [6]. Similarly, the gait sub-phase information has been used by various application devices such as functional electronic stimulation [7-11], wearable limb exoskeleton [12-16], and powered prostheses [17-20] which support subjects with gait anomalies. These applications utilise the sub-phase level information to enable patients with spinal cord injuries to walk and also enhance the performance of healthy subjects.

Despite the vast application areas of gait segmentation, it has been a challenging task more specifically for pathological gait [5]. In general, detecting the gait events that mark the transition from one gait sub- phase to another as well as the sequence of gait sub-phases is essential to evaluate gait abnormalities [21]. Literature consists of a number of approaches to classify the gait sub-phases in a normal walking gait. For instance, support vector machines, artificial neural networks [22], hidden Markov models [23-26], fuzzy models [27,28], and simple heuristic threshold methods [9,20] have been employed for gait sub-phase segmentation. These methods use variety of wearable sensors that include accelerometers [29], gyroscopes and force sensing resistors [9], inclinometers [30], and other force-contact sensors [31] for the gait data acquisition. Although, the aforementioned gait segmentation methods have been performed efficient sub-phase level gait segmentation; these are limited to healthy subjects (i.e. normal gait) only.

On the other hand, pathological gait segmentation has been a challenging task [5] because of its varying features for different patients and corresponding gait anomalies. The literature contains a variety of approaches to segmenting the abnormal gait into subphases [5,32-36]. For instance, Jasiewicz et al. [32] proposed an algorithm for gait event (initial contact and end contact) detection in healthy and spinal-cord injured subjects. A number of methods were implemented using foot linear acceleration, foot sagittal angular velocity, and shank sagittal angular velocity data and their performances were compared with the most commonly used foot switch based gait data. Effective event detection was achieved for normal footfall patterns which are reduced significantly in pathological gaits specifically those involving the use of walking aids. Similarly, a pathological gait cycle segmentation presented in Agostini et al. [5].

performs the task of partitioning input signal into multiple gait cycles followed by the determination of atypical gait cycle in a foot switch signal. The anti-causal anti-bounce filter was used to eliminate the spurious spikes from the input signal. The processed signal is auto-segmented into four sub-phases that include heel contact, flat foot contact, heel-off, and swing. The duration of each gait cycle is measured by integrating the number of samples in its sub-phases which is then used for atypical gait cycle recognition. This method was tested on healthy as well as pathological gait cycles acquired from patients with Parkinson’s disease and Hemiplegic children. Despite the efficient performance, these methods are able to segment the gait cycle up to a limited (two to three) number of sub-phases. These methods are also applicable to a specific type of pathology.

This manuscript introduces a novel approach used in the CORBYS system to perform multiple tasks that include: (i) partition of the joints’ angular data into separate gait cycles (ii) identification of the pathological gait cycle based on the acquired signal during walking (iii) and finally segmentation of the pathological and healthy gait into sub-phases. In the case of pathological gait, the degree of deviation (i.e. anomaly level) in each sub-phase is measured to be used for medical treatment (i.e. gait rehabilitation). The segmentation and classification of pathological gait cycles becomes difficult because of associated dynamics for different patients and corresponding gait anomalies. In this scene, the proposed method introduces a generic gait segmentation applicable to both; healthy and pathological subjects having different types of anomalies, since the segmentation process is carried out without the definition of gait sub-phases templates. Time domain features are extracted from the acquired hip-joint angular data for sagittal movement and utilized to divide the automated gait segmentation into seven subphases. The degree of anomaly is then estimated at sub-phase level with respect to an optimal reference to find out the pathology type and exact location in the gait cycle.

Data acquisition and pre-processing

Figure 1:Gait coordinate system in CORBYS to acquire and analyse the joint motion data.

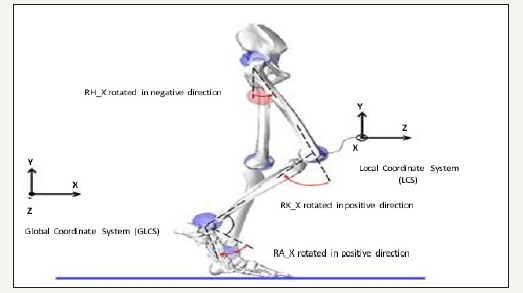
The gait data for healthy and disabled patients has been recorded by the CORBYS clinical partners URIRS2. Data was recorded using the VICON motion capture system which logs the motion of infra-red sensitive markers strategically placed on the patients. Synchronised sensor readings are transmitted wirelessly formatted as standardised Robot Operating System (ROS) data from the human sensory system controller. Markers measure the motion within particular axes of the gait motion. This clinical data comprises the motion data relayed to the feed-forward trajectory controller for calculation of joint moments for the human body model. The coordinate system for this gait data is described in Figure 1 which depicts gait measured along three planes of motion. The sagittal plane describes motion around x- axis, the transversal plane describes motion around y-axis, and the frontal plane describes motion around the z-axis. The acquired dataset consists of measurements for each joint in both legs recorded in selected planes. Hip data is recorded in all three axes, knee data is recorded in only x-axis, and ankle data is recorded in the x-axis and z-axes.

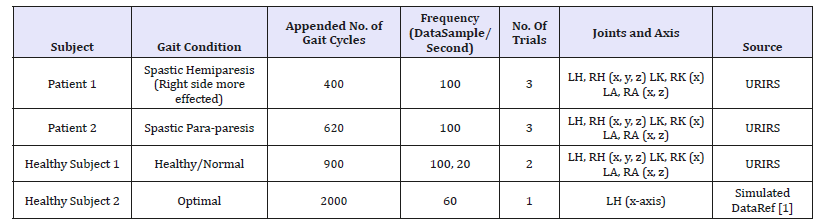
The initial motion data for two patients are five to eight seconds of duration and contain six to eight gait cycles. The duration of a gait cycle is limited by the size of the recording area of the motion capture system. The URIRS does not record patients on the treadmill and therefore we have to append several gait cycles in order to obtain longer datasets of disabled gait. However, a large dataset for healthy subjects was recorded by walking on a treadmill. In addition, simulated data is generated using the optimal gait ranges [1] for joint muscular motion. Details of the appended motion data for one healthy subject, two patients, and a simulated dataset are presented in Table 1.

Table 1:Data characteristics.

FOOT NOTE<

²University of rehabilitation institute, republic of slovenia;http://www.irrs.si/en/Research_and_development_unit/

Gait analysis and anomaly detection

Figure 2:Body positions and corresponding hip, knee, and ankle joints sagittal dimension activities in both legs for a complete gait cycle and sub-phases within the swing and stance phases. from left to right, figure demonstrates the side view of synchronised joints motion and transitions between sub-phases in a healthy gait cycle.

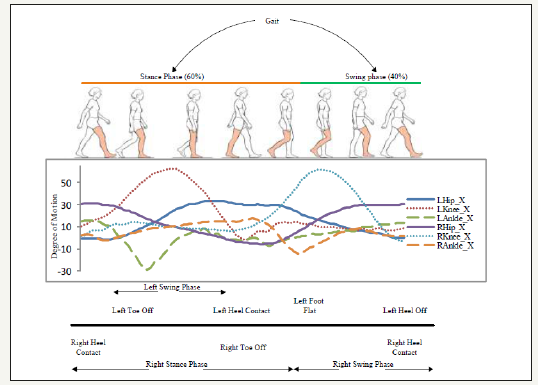
Gait model employed in the proposed study is a classic gait model by Perry [2] which divides each cycle into seven sub-phases that include: Initial Contact (IC) to Load Response (LR), Mid Stance (MSt), Terminal Stance (TSt), Pre Swing (PSw), Initial Swing (ISw), Mid Swing (MSw), and Terminal Swing (TSw). Figure 2 demonstrates a complete gait cycle acquired for healthy subject in Table 1, transitions between its sub-phases, and corresponding left hip, knee, and ankle joint movements in sagittal dimension.

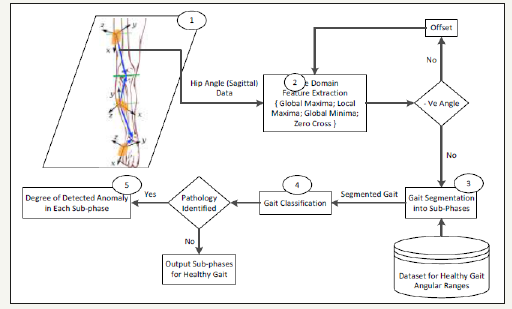
Hip flexion and extension are one of the most important muscular activities in the walking phenomenon that occur with the pelvic girdle forward and backward rotation in the hip flexion and extension respectively [37-39]. It can be observed in Figure 2 that the Hip joint motion, specifically in sagittal dimension is a necessary condition for the body to move forward. In other words, without the Hip sagittal motion, a subject cannot progress (i.e. step forward or backward) along a horizontal axis regardless of gait medical conditions. This implies that maximum and minimum values for Hip joint sagittal dimension angular motion indicate the flexion and extension extremes of the corresponding leg respectively in a gait cycle. Hence, the proposed method exclusively processes the Hip joint muscular activities to partition and segment the gait cycle. A number of time-domain features are extracted from the acquired Hip-joint motion data (sagittal dimension only) to segment the entire gait into sub-phases. These features include global maxima, global minima, zero cross index, and offset value along with the expert knowledge from the literature [1,40,41] for joint motion ranges. Figure 3 shows sequential processing of the proposed method to partition, sub-phase level segmentation, and classification (healthy/pathological) of a gait cycle which is further used to measure the degree of deviation in the effected sub-phase.

Figure 3:Sequential processing of the proposed method for (1) Data acquisition; (2) Feature extraction; (3) Gait segmentation into sub-phases; (4) Classification of the gait into healthy and abnormal gait using hip muscular activities; (5) Measurement of anomaly type, degree, and exact event in terms of sub-phase.

The proposed gait segmentation algorithm using time domain features of Hip joints sagittal dimension motion data is described below.

Input and output:

1) 2-dimensional vector X_Lhip,Rhip for Hip-joints angular data

2) Vector Gp for partitioned gait cycles start and end points

3) Segmented gait Gsub into 7 sub-phases

Algorithm steps:

1) Find index of the 1st negative-going ZCR- sample in X_Lhip if there is and set as terminal-stance start TSt_ s

2) In case of no ZCR-, find the minimum value ( X_min) in X_Lhip, shift the entire vector by an offset of offset min offset = (−5 − X ) and perform the above step

3) Find index of the 1st positive-going ZCR+ sample in X_Lhip after TSt_s and set as initial-swing start ISw_s

4) Find minimum value sample index between TSt_s , ISw_s and set as pre-swing start PSw_s

5) Find index of the 1st negative-going sample ZCR- in X_Lhip after ISw_s and set as end of 1st gait cycle Gend

6) Find minimum value sample in X_Rhip index in-between ISw_ s and Gend. Then find the corresponding index in X_Lhipand set as mid-stance start MSt_ s

7) Find index of maximum value sample between ISw_s & MSt_s and set as terminal-swing start TSw _s

8) Set the mid-point between ISw_s and TSw_s as mid-swing start MSw_s

9) Make segment of each sub-phase using the calculated start points and assign the output vector Gsub containing start and end index for each sub-phase. For instance, G_Mst = X_Lhip _ indexes (MSt _ s to Gend ) and so on

10) Finally, revert the entire gait sub-phases to original level if offset is applied in the first step.

A visual demonstration of the described algorithm is presented in Figure 4. The interval between two successive negative going Zero-Crossing Rate (ZCR) produces a complete gait cycle. Following the ZCR- which represents the start of the TSt as the initial point, 1st positive data sample after ZCR gives the index of positive-going zero-cross (ZCR+) that represents the end of PSw sub-phase. The index of minimum data sample (Gmin) between ZCR- and ZCR+ is then calculated that gives the end of the TSt. In the next step, the index of the LR segment is calculated using the opposite leg angular data. As the data is synchronised, the index in the left Hip data corresponding to the minimum data sample in the right Hip will produce the finishing point of the LR sub-phase. To assure the synchronization in terms of being within the same gait cycle, the IC_LR index is calculated between the indexes of ZCR+ and the end of the gait cycle as shown in Figure 4 above. The index of the data sample with a maximum value (G^max) between ZCR+ and IC_LR is then calculated which indicates the starting index of TSw. Finally, data samples between IC_LR and the end of the gait cycle (2nd ZCR-) indicates the MSt which is the longest sub-phase in a gait cycle.

Figure 4:A visual representation of aforementioned gait segmentation algorithm using minima, maxima, offset, and zero crossings features extracted from left and right hip x-axis motion data.

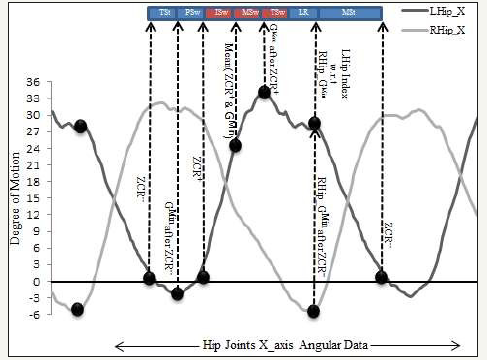
An important aspect of the proposed method is the ability to segment the gait with many types of pathology since training on the pathology specific templates is not required. To increase the reliability of the proposed algorithm, a number of important checks are carried out specifically for pathological gaits.

For example, the data synchronisation check is performed prior to sub-phase classification as described earlier. Likewise, an offset value is used to ensure that the corresponding leg always crosses the pelvis point (origin) in the sagittal dimension that pursues the Hip flexion and extension phenomenon. The importance of the offset check can be analysed in Figure 4 which indicates that the gait segmentation uses zero crossings. In the case of a healthy subject, the gait always performs positive and negative angular activities which may not be the case for a pathological gait. In order to rectify this, we use an offset value to shift the entire gait by the required amount according to optimal gait ranges [1,40,41]. After the subphases measurements, the offset value is reused with a reverse sign to revert the signal into its original form. The degree of deviation in each sub-phase is then measured using the optimal gait ranges as a reference. The Euclidean distance between the sub-phases of the test subject and optimal reference gives the anomaly in a particular sub-phase that is further used for gait rehabilitation and the decision controller in the CORBYS system [42,43].

Experimental setup and evaluation methodology

Experiments were conducted on the dataset presented in Table 1 using the proposed algorithm described earlier. The acquired data was forwarded to sequential setup presented in Figure 2 to achieve the desired goal of sub-phases classification. MATLAB® by Math works was used for data processing, analysis, and simulation purposes. The validation process aims to demonstrate that the algorithm is as good as the human expert. The algorithm was validated on a total of 3920 gait cycles; 2900 from healthy and 1020 from pathological subjects) using the manual and automated methods presented in Agostini et al. [5]. For each signal, we compared the gait cycle classification obtained from the proposed algorithm and “manual” segmentation. The manual segmentation was performed with the following steps: (1) Extract the Hip joints X-axis motion data from the acquired ROS bags (2) Store in Excel sheets and mark each gait with a segmentation line (3) Label the dataset with a corresponding gait cycle number and sub-phases. Algorithm output can be classified in the binary form of correct and incorrect segmentation of a sub- phase. When a new sub-phase is incorrectly classified by an algorithm, a cross is added on a sheet of paper near the corresponding sub-phase name (4) Counting the crosses assigned to each sub-phase segment, we calculated the mismatched sub-phases between the procedures (i.e. algorithm and manual segmentation) if present. Performance of the algorithm was defined as the number of sub-phases matching the manual segmentation divided by the total number of sub-phases. Likewise, the performance of the healthy subject and self-generated dataset is evaluated by varying the tolerance window in terms of sub- phase start and end position estimates.

Table 2:Overall statistical results for optimal and pathological gait segmentation and classification for varying temporal tolerance window.

The proposed gait segmentation algorithm is applied to the sample dataset and results were obtained as reported in Table 2. For each examined subject, we indicated the subject’s health condition, accuracy for complete cycle partition in the gait data through manual and automatic procedures, the classification accuracy for a gait to be recognised as normal or pathological, and accuracy of sub-phase level segmentation for healthy and patient gait data corresponding to the varying temporal tolerance window.

Time period of the oscillations in the gait data also varies depending on how fast the patient is walking. Additionally, from left to right leg, qualitatively the dynamics become more erratic. This is likely due to the increased degrees of freedom and variability of movement and the successive dependency of the left hip dynamics on those of the right hip; specifically, for the LR sub-phase. Taken together, these factors make the learning of a patient’s gait challenging [5]. The extreme indexes for sub-phases in ground truth and algorithm output may lag by a number of samples. The varying tolerance window indicates granularity in the system performance for sub-phases segmentation as shown in Table 2. This phenomenon can be analysed in Table 2 results where the accuracy is affected only during the TSw and LR sub-phases. Statistics indicated that the system performance degraded 003% when the tolerance level is decreased from 6% to 3% of the gait cycle. However, the proposed algorithm classified, partitioned, and segmented 100% of the cycles in healthy subjects and over 99% in pathological subjects which demonstrate that the muscular activities of Hip joints can be used for sub-phase level segmentation for both healthy and pathological gaits. These results indicate the superiority of our algorithm in terms of the segmentation accuracy and granularity level of seven sub-phases as compared to the existing signal processing [32,34,35] and machine learning [22,23,25,26] based approaches that are limited to segment the gait cycle into up to three subphases. Despite of the accuracy (100% and 98% for healthy and pathological subjects respectively) achieved by Agostini et al. [5] in terms of gait segmentation and classification into normal and pathological, it was limited to three sub-phases only which decreases the granularity level of gait rehabilitation.

Angular ranges for the joint muscles in a healthy gait vary with respect to subject physical properties and other dynamics [1,40]. For instance, in left Hip sagittal motion, it varies from 30 to 35 in flexion and -2 to -10 in the extension phase. This gives an indication to set the anomaly threshold for each sub-phase to classify a gait cycle as normal or pathological. For instance, the gait classification results shown in Table 2 are achieved using a threshold value of ±5 degree which means that a gait is identified as pathological if any of its sub-phases deviate more than 5 degrees (flexion or extension). However, the threshold value may vary with respect to application, patient condition, and rehabilitation process. The efficient subphase level segmentation is very useful for detecting the exact spatial and temporal position of defected gait as shown in Table 3. It can be observed that the mean deviations of the patient sub-phase from the optimal gait are larger than in a healthy gait. For instance, the MSw for patient 1 is deviated 8.07 degrees in the sagittal dimension which indicates the required degree of rehabilitation in the left Hip joint sagittal dimension in that particular sub-phase. Also, diminutive deviations within the anomaly threshold for healthy subjects as expected; validate the proposed method for healthy gait segmentation.

Table 3:Comparison of statistical results for healthy and pathological subject’s degree of anomaly per sub-phase of gait cycles, gait partition, and healthy/pathological gait identification.

An accurate segmentation of gait sub-phases is useful for several scientific studies such as the assessment of the gait anomaly level in patients after interventions or rehabilitation treatments and distinguishing between a normal and pathological gait [2,4]. Figure 5 demonstrates a test case outcome for healthy and pathological gait segmentation into seven sub-phases. The degree of deviation in each sub-phase can be easily observed and calculated which indicates the anomaly type and location in a pathological gait cycle. For instance, the TSt and PSw phases of both patients are an approximately deviated mean value of 10 degrees with respect to the optimal reference which indicates that the rehabilitation is needed for these two sub-phases only.

This research was focused on the gait segmentation into seven sub-phase using Hip joint angular motion independent of a pathology type. The proposed method was able to partition the continuous stream of Hip joint sagittal dimensional motion data into individual gait cycles and classify the gait as normal or pathological based on the measured degree of anomaly in each sub-phase. The Sub-phase level gait segmentation enabled the determination of the deviation in a patient’s gait from the optimal reference gait pattern. The measured deviation provided the required information for the gait rehabilitation system to make inferences regarding what supportive actuation needs to be applied at which point in the walk cycle to improve the patient’s gait as best suited to the condition consistent with the clinical judgement of the gait therapist. These outcomes also serve as an enabler for future research on different aspects. For instance, multiple joint muscular activities may be combined together to produce a more reliable gait segmentation.

1. Vaughan CL, Davis BL, O’Connor JC. Dynamics of human gait, (2nd edn), Kiboho Publishers, South Africa.
2. Perry J (1992) Gait analysis: Normal and pathological function. SLACK Incorporated: Thorofare, New Jersey, USA, p. 3-47.
3. Rueterbories J, Spaich EG, Larsen B, Andersen OK (2010) Methods for gait event detection and analysis in ambulatory systems. Med Eng Phys 32(6): 545-552.
4. Taborri J, Palermo E, Rossi S, Cappa P (2016) Gait partitioning methods: A systematic review. Sensors 16(1): 66.
5. Agostini V, Balestra G, Knaflitz M (2014) Segmentation and classification of gait cycles. IEEE Trans Neural Sys and Rehabilitation Eng 22(5): 946- 952.
6. Jung JY, Heo W, Yang H, Park H (2015) A neural network-based gait phase classification method using sensors equipped on lower limb exoskeleton robots. Sensors 15(11): 27738-27759.
7. Marsolais EB, Kobetic R (1987) Functional electrical stimulation for walking in paraplegia. J Bone Joint Surgery Am 69(5): 728-733.
8. Willemsen ATM, Bloemhof F, Boom HBK (1990) Automatic stance-swing phase detection from accelerometer data for peroneal nerve stimulation. IEEE Trans Biomed Eng 37(12): 1201-1208.
9. Pappas, IPI, Popovic MR, Keller T, Dietz V, Morari M (2001) A reliable gait phase detection system. IEEE Trans Neural System Rehabilitation Engineering 9(2): 113-125.
10. Mansfield A, Lyons GM (2003) The use of accelerometer to detect heel contact events for use as a sensor in FES assisted walking. Med Eng Phys 25(10): 879-885.
11. Hanlon M, Anderson R (2009) Real-time gait event detection using wearable sensors. Gait Posture 30(4): 523-527.
12. Suzuki K, Mito G, Kawamoto H, Hasegawa Y, Sankai Y (2007) Intention-based walking support for paraplegia patients with Robot Suit HAL. Adv Robot 21: 1441-1469.
13. Díaz I, Gil JJ, Sánchez E (2011) Lower-limb robotic rehabilitation: Literature review and challenges. Jour Robot, pp. 1-11.
14. Jung J, Jang I, Riener R, Park H (2012) Walking intent detection algorithm for paraplegic patients using a robotic exoskeleton walking assistant with crutches. Int Jour Control Auto Sys 10: 954-962.
15. Hassan M, Kadone H, Suzuki K, Sankai Y (2013) Wearable gait measurement system with an instrumented cane for exoskeleton control. Sensors 14(1): 1705-1722.
16. Lu R, Li Z, Su CY, Xue A (2014) Development and learning control of a human limb with a rehabilitation exoskeleton. IEEE Trans Ind Electron 61(7): 3776-3785.
17. Martinez VEC, Herr H (2009) Agonist-antagonist active knee prosthesis: A preliminary study in level- ground walking. Jour Rehabilitation Res Dev 46(3): 361-373.
18. Varol HA, Sup F, Goldfarb M (2010) Multiclass real-time intent recognition of powered lower limb prosthesis. IEEE Trans Biomed Eng 57(3): 542- 551.
19. Lawson BE, Varol HA, Goldfarb M (2011) Standing stability enhancement with intelligent powered trans femoral prosthesis. IEEE Trans Biomed Eng 58(9): 2617-2624.
20. Goršič M, Kamnik R, Ambrožič L, Vitiello N, Lefeber D, et al. (2014) Online phase detection using wearable sensors for walking with a robotic prosthesis. Sensors 14: 2776-2794.
21. Pons JL, Moreno JC, Brunetti FJ, Rocon E (2007) Lower-limb wearable exoskeleton, rehabilitation robotics. In: Sashi SK (Ed.), ISBN: 978-3- 902613-04-2, In Tech.
22. Mijailoviü N, Gavriloviü M, Rafajloviü S, Popoviü DB (2009) Gait phases recognition from accelerations and ground reaction forces: Application of neural networks. Telfor Journal, 1(1): 34-36.
23. Mannini A, Sabatini AM (2012) Gait phase detection and discrimination between walking-jogging activities using hidden Markov models applied to foot motion data from a gyroscope. Gait Posture 36(4): 657-661.
24. Mannini A, Sabatini AM (2011) A hidden markov model-based technique for gait segmentation using a foot-mounted gyroscope. Int Conf IEEE Eng Med and Bio Soc 2011: 4369-4373.
25. Meng M, She Q, Gao Y, Luo Z (2010) EMG signals based gait phases recognition using hidden Markov models. IEEE Int Conf Inf and Aut, Harbin, China, pp. 852-856.
26. Rossi SMD, Crea S, Donati M, Reberšek P, Novak D, et al. (2012) Gait Segmentation Using Bipedal Foot Pressure Patterns. 4th IEEE RAS/EMBS Int Conf Bio Rob and Bio, Roma, Italy, pp. 361-366.
27. Kong K, Tomizuka M (2008) Smooth and continuous human gait phase detection based on foot pressure patterns. Proc IEEE Int Conf Rob and Automation 2008, Pasadena, CA, USA, pp. 3678-3683.
28. Agostini V, Luca RD, Mansin LC, Knaflitz M (2012) Reduction of gait abnormalities in type 2 diabetic patients due to physical activity: a quantitative evaluation based on statistical gait analysis. Jour Mech Med Biol 12(5): 1-10.
29. Williamson R, Andrews BJ (2000) Gait event detection for FES using accelerometers and supervised machine learning. IEEE Trans on Rehabilitation Eng 8(3): 312-319.
30. Rueterbories J, Spaich EG, Larsen B, Andersen OK (2010) Methods for gait event detection and analysis in ambulatory systems. Med Eng Phys 32(6): 545-552.
31. Kong K., Tomizuka M (2009) A gait monitoring system based on air pressure sensors embedded in a shoe. IEEE/ASME Tran Mechatronics 14(3): 358-370.
32. Jasiewicz JM, Allum JHJ, Middleton JW, Barriskill A, Condie P, et al. (2006) Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals. Gait & Posture 24(4): 502-509.
33. Abaid N, Cappa P, Palermo E, Petrarca M, Porfiri M (2013) Gait detection in children with and without hemiplegia using single-axis wearable gyroscopes. PLoS ONE 8(9): e73152.
34. Mariani B, Rouhani H, Crevoisier X, Aminian K (2013) Quantitative estimation of foot-flat and stance phase of gait using foot-worn inertial sensors. Gait Posture 37(2): 229-234.
35. Han J, Jeon H, Jeon B, Park K (2006) Gait detection from three dimensional acceleration signals of ankles for the patients with Parkinson’s disease. Proc IEEE Int Special Topic Conf on Inf Tech in Biomed 2006, Ioannina, Greece, 2628, pp. 1-4.
36. Moulianitis VC, Syrimpeis VN, Aspragathos NA, Panagiotopoulos EC (2011) A closed-loop drop- foot correction system with gait event detection from the contralateral lower limb using fuzzy logic. In Proc of 10th Int Work on Biomed Eng, Kos, Greece, pp. 1-4.
37. Crosbie J, Vachalathiti R (1997) Synchrony of pelvic and hip joint motion during walking. Gait and Posture 6(3): 237-248.
38. https://www.kean.edu/~jeadams/docs/Kinesiology/Kines_Power_ Points/Kines_Chap_9.pdf
39. Taylor T (2012) Hip joint: Inner body.com, How to media, Inc.
40. Kirkwood RN, Gomes HA, Sampaio RF, Culham E, Costigan P (2007) Biomechanical analysis of hip and knee joints during gait in elderly subjects. Acta Ortop Bras 15(5): 267-271.
41. Manuela G, Chiara R, Reinald B, Naznin VB, Albertini G (2008) Stiffness and gait pattern evaluation in children with Down syndrome. Gait & Posture 28(3): 502-506.
42. Liverud AE, Dalgard S, Fleurey F, Vedum J, Morten HR, et al. (2015) A multimodal human sensory system to support mobile gait rehabilitation. Technically Assisted Rehabilitation Conference.
43. Badii A, Khan A, Raval R, Oudi H, Ayora R, et al. (2014) Situation assessment through multi-modal sensing of dynamic environments to support cognitive robot control. Facta Universitatis Series, Mechanical Engineering 12(3): 251 -260.