- Submissions

Full Text
Research in Medical & Engineering Sciences
Energy Criteria for Structural Interactions with Free Radicals
GА Korablev*
Doctor of Chemical Sciences, Russia
*Corresponding author: GА Korablev, Doctor of Chemical Sciences, Russia
Submission: December 17, 2018; Published: December 20, 2018

ISSN: 2576-8816Volume7 Issue2
Abstract
Spatial-energy characteristics of many molecules and free radicals are obtained. The possibilities of applying the P-parameter methodology to structural interactions with free radicals and photosynthesis energetics evaluation are discussed. The satisfactory compliance of calculations with experimental and reference data on main photosynthesis stages is shown.
Keywords: Spatial-energy parameter; Free radicals; Structural interactions; Photosynthesis
Designations
m1 and m2-masses of material points (kg); а - their acceleration (m/S2); Δх - coordinate (m); ΔU1 and ΔU2 potential energies of material points (J); ΔU - their resulting (mutual) potential energy of interaction (J); Z* - nucleus effective charge (Cl); n* - effective main quantum number; Wi - bond energy of electrons on i-orbital (eV); ri - orbital radius of i-orbital (Å); ni - number of electrons on this orbital; SEI - spatial-energy interactions; P0 - spatial-energy parameter (eVÅ); PE - effective Р-parameter (eV); R - dimensional characteristic of atom or chemical bond (Å); N1, N2, … - number of homogeneous atoms; PC - Р-parameter of complex structure (eV); Ψ - Ψ-function; α - coefficient of structural interactions, isomorphism (%); ρ - degree of structural interaction (%).
Introduction
Free radicals are the atom groups or molecule fragments having unpaired electrons. Most of them are unstable with high reactivity. Interacting between themselves and with other molecules they produce new compounds that continue chemical reactions based on chain principle - like neutrons in chain nuclear reactions. In many cases such processes are the main reason of pathologic condition of living systems [1].
Therefore, the problem of searching “retardants” for these chain reactions of free radicals is critical. For instance, it is known that sulfur-containing amino acid (cysteine) “attracts” unpaired electrons of protein [2,3]. Similar properties are reported about selenium, the element of the same subgroup VI-а of the System as sulfur [4]. It is found out that the number of unpaired electrons in dry bio-objects (after their production) decreases when introducing nitric oxide or increasing the moisture content.
On the contrary, the role of oxygen atoms (also the element of VI-а subgroup of the System) is often expressed as the role of an accelerator of irreversible reactions of free radicals. Free radicals (including oxygen) demonstrate specific influence in complicated bio-physicochemical processes of photosynthesis. Fundamental regularities of reactions with free radicals were found by I.I. Semenov and his disciples. Important contribution to solving the problem of free radical participation in biological processes was made by NM Emmanuel, АG Gurvich, BN Tarusov, LА Bluemenfeld, GМ Frank, W Gordy, B Commoner, MJ Calvin and others. It seems interesting to find a functional dependence and directedness of free-radical processes with initial energy and dimensional characteristics of their atoms-components. In this paper we are attempting to explain such processes applying the methodology of spatial-energy notions (P-parameter).
Methodology Substantiation
Comparing multiple regularities of physical and chemical processes we can assume that in many cases the principle of adding reciprocals of volume energies or kinetic parameters of interacting structures is implemented. Some examples: ambipolar diffusion, total rate of topochemical reaction, change in the light velocity when transiting from vacuum into the given medium, resulting constant of chemical reaction rate (initial product - intermediary activated complex - final product).
Lagrange equation for relative movement of isolated system of two interacting material points with masses m1 and m2 in coordinate х with acceleration α can be presented as follows:

Where ΔU1 and ΔU2 - potential energies of material points in elementary section of interactions, ΔU - resulting (mutual) potential energy of these interactions.
The atom system is formed from oppositely charged masses of nucleus and electrons. In this system energy characteristics of subsystems are the orbital energy of electrons (wi) and effective energy of nucleus that takes into consideration the screening effects (by Clementi). Therefore, assuming that the resultant interaction energy of the system orbital-nucleus (responsible for interatomic interactions) can be calculated based on the principle of adding reciprocals of some initial energy components, we substantiate the introduction of P-parameter [5] as an averaged energy characteristic of valence orbitals in accordance with the following equations:
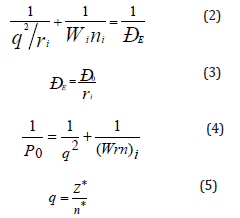
Here: Wi - bond energy of electrons [6]; ri - orbital radius of i-orbital [7]; ni - number of electrons of the given orbital, Z* and n* - effective charge of nucleus and effective main quantum number [8]. The P0 value will be called a spatial-energy parameter, and the PE value - effective Р-parameter. Effective PE-parameter has a physical sense of some averaged energy of valence electrons in atom and is measured in energy units, e.g. in electron-volts (eV).
Based on the results [5] the values of PE-parameters numerically equal (within 2%) total energy of valence electrons (U) by the atom statistic model. Using the well-known ratio between electron density (β) and inneratomic potential by the atom statistic model, we can obtain the direct dependence of PE-parameter upon the electron density at the distance ri from the nucleus:

Validity of this equation was confirmed when calculating the electron density using Clementi’s wave functions and comparing it with electron density value calculated via PE-parameter value. Besides the modules of maximum values of ψ-function radial part were compared with P0-parameter values, and the line dependence between these values was found. Using some properties of wave function for P-parameter, the wave equation of P-parameter was obtained.
Based on calculations and comparisons two principles of adding spatial-energy criterions depending upon wave properties of P-parameter and systemic character of interactions and charges of particles were substantiated:
a) Interaction of oppositely-charged (heterogeneous) systems consisting of I, II, III, ... atom sorts is satisfactorily described by the principle of adding corresponding energy reciprocals by equations (2-5) (this corresponds to the minimum of weakening oscillations taking place in antiphase);
b) During the interaction of similarly-charged (homogeneous) subsystems the principle of algebraic adding of their P-parameters is realized based on the following equations:
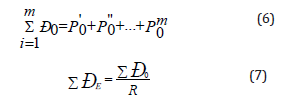
where R -dimensional characteristic of atom (or chemical bond).
This principle corresponds to the maximum of oscillation intensification taking place in the phase. Modifying the rule of adding energy reciprocals of subsystems as applied to complex structures we can obtain the equation for calculating PC-parameter of complex structure:
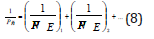
Where N1 and N2 - number of homogeneous atoms in subsystems.
During the formation of solution and other structural interactions the same electron density must be formed in the areas of contact of atoms-components. This process is accompanied by the redistribution of electron density between valence zones of both particles and transition of a part of electrons from some outer spheres into neighboring ones. Apparently, spanning electrons of atoms do not participate in such an exchange.
Apparently, with the closeness of electron densities in free atoms-components, the transition processes between boundary atoms of particles will be minimum, thus favoring the formation of new structure. So, the evaluation of the degree of structural interactions in many cases comes to the comparative evaluation of electron density of valence electrons in free atoms (on averaged orbitals) participating in the process.
The less is the difference (Р’0/r’i - P”0/r”i), the more favorable is the formation of a new structure or solid solution from energy point.
In this connection the maximum total solubility evaluated through the coefficient of structural interaction a is defined by the condition of minimum value of a that represents a relative value of effective energies of outer orbitals of interacting subsystems:
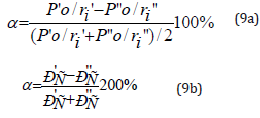
The nomogram of dependence of structural interaction degree (ρ) upon the coefficient α, unified for a broad range of structures was designed based on all the data obtained. Figure 1 shows the nomogram obtained using PE-parameters calculated via the bond energy of electrons (wi) for structural interactions of isomorphic type. Following this methodology the mutual solubility of atomscomponents was evaluated in many (over a thousand) simple and complex systems. The calculation results agree with reference and experimental data.
Figure 1:Nomogram.
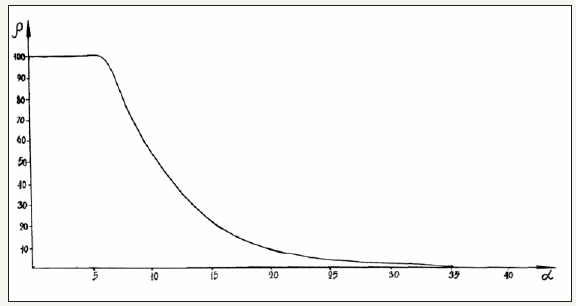
Isomorphism as a phenomenon is used to be applied to crystalline structures. Apparently, analogous processes can also take place between molecular compounds where their role and significance are no less than of purely coulomb interactions.
In complex organic structures the main role can be performed by separate “blocks” or fragments. Therefore, the task is to identify these fragments and evaluate their spatial-energy parameters. According to wave properties of Р-parameter, total Р-parameter of each fragment must find based on the principle of adding reciprocals of initial P-parameters of all the atoms. The resultant Р-parameter of fragment block or all the structure is calculated following the rule of algebraic adding of P-parameters of fragments constituting them.
The role of fragments can be performed by valence-active radicals, e.g. СН, СН2, (ОН)-, NO, NO2, (SO4)2-, etc. In complex structures this carbon atom usually has not one, but two or three side bonds. The priority significance when calculating based on the principle of adding reciprocals of P-parameters have those bonds, for which the condition of interference minimum is better executed. Therefore, first the fragments of bond С-Н (for СН, СН2, СН3 …) are calculated, and then separately the fragments N-R, where R-binding radicals (e.g. - for the bond C-N).
Apparently, spatial-energy interactions (SEI) based on equalization of electron densities of valence orbitals of atomscomponents have in nature the same universal significance as purely electrostatic coulomb interactions, but they supplement each other. Isomorphism known from the time of Micherlikh E 1820 and Mendeleev DI 1856 is only a particular manifestation of this overall natural phenomenon. The quantitative side of evaluating isomorphic replacements of components, both in complex and simple systems, can be rationally placed in the frameworks of P-parameter methodology. The problem of evaluating the degree of structural SEI for molecular and organic structures is more complicated. The methodology for calculating P-parameters of molecules, structures and their fragments are successfully implemented [5]. But such structures and their fragments are not often completely isomorphous to each other. Nevertheless, SEI proceeds between them, its degree can be evaluated only semiquantitatively or qualitatively. All systems can be split into three types based on their isomorphous similarity:
1. Systems mainly isomorphous to each other - the systems with almost the same number of heterogeneous atoms and summarily similar geometric shapes of interacting orbitals.
2. Systems with limited isomorphous similarity - the systems that:
a) either differ in the number of heterogeneous atoms but have summarily similar geometric shapes of interacting orbitals;
b) or definitely differ by geometric shape of orbitals but have the same number of interacting dissimilar atoms.
3. Systems without isomorphous similarity - the systems that considerably differ both in number of dissimilar atoms and geometric shape of their orbitals.
Then, considering some experimental data, all types of SEI can be approximately classified as follows:
Systems I
a) α < (0-6)%; ρ = 100%.
Complete 100% isomorphism, complete isomorphous replacement of atoms-components;
b) 6% < α < (25-30)%; ρ = 98 - (0-3)%.
Either broad or limited isomorphism as shown in nomogram 1;
c) α > (25-30) %; no SEI
1.1. Systems II
a) α < (0-6)%;
i. Reconstruction of chemical bonds, can be accompanied with the formation of a new compound;
ii. Breaking of chemical bonds can be accompanied with the separation of a fragment from the initial structure, but without joining or replacing.
b) 6 % < α < (25-30)%;
A limited internal reconstruction of chemical bonds without the formation of a new compound and replacements is possible.
c) α > (20-30)%; no SEI
Systems III
a) α < (0-6)%;
i. Limited change in the type of chemical bonds of the given fragment, internal regrouping, without breaking from the main part of the molecule and replacements is possible;
ii. Some dimensional characteristics of the bond can change;
b) 6% < α < (25-30)%;
A very limited internal regrouping of atoms;
c) α > (25-30)%; no SEI.
Nomogram № 1 is made for isomorphous interactions, i.e. for such structures or subsystems with the same number of dissimilar atoms and approximate geometric resemblance of interacting atomic orbitals. In all other cases the calculated values of α and ρ refer only to the given type of interactions, nomogram of which is not yet existing, and all the comparisons are merely assumptions of qualitative or semi-quantitative character.
But if taking into account the universality of spatial-energy interactions in nature, this evaluation can be significant for analyzing structural rearrangements in complex bio-physicochemical processes (this will be further shown on the example of photosynthesis). Enzymatic systems can greatly contribute to the correlation of the degree of structural correlations. In this model the enzyme role is as follows: active parts of its structure (fragments, atoms, ions) the PE-parameter value equal to the PE-parameter of the reaction final product. I.e. the enzyme is structurally “tuned” via ПЭВ to obtaining the reaction final product but will not join it due to imperfect isomorphism of its structure (in accordance with III).
Calculations and Comparisons
Based on equations (2-5) with initial data calculated with quantum-mechanical techniques [6-8], the values of P0-parameters of the majority of elements being tabulated constant values for each valence atom orbital were calculated. Mainly covalent radii were applied as a dimensional characteristic for calculating PE-parameter - by main type of chemical bond of interactions considered (Table 1). For hydrogen atom also, the value of Bohr radius and value of atomic (“metal”) radius were applied.
Table 1:Р-parameters of atoms calculated via bond energy of electrons.
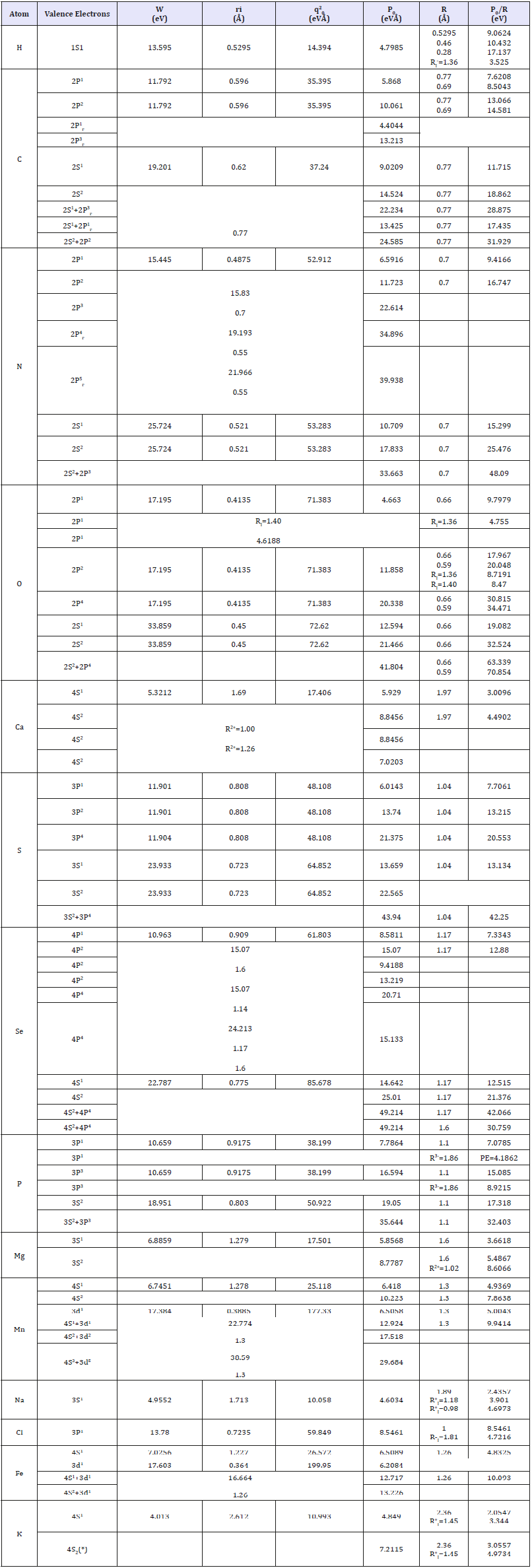
In some cases, the calculations of P-parameters are given considering the possibility of hybridization of atom orbitals (marked with “Г”) - following the methodology discussed before [9]. Besides we took into account the bond repetition factor for carbon and oxygen atoms. In the course of calculations for potassium atom - element of group IV of large periods in the System the possibility of the influence of internal d-orbitals was considered. For several elements the values of PE-parameters were calculated using ionic radii whose values are given in column 7. All the values of atomic, covalent and ionic radii are basically taken by Belov-Bokiy [10], but crystalline ionic radii - by Batsanov [10].
Table 2 contains the computational results of structural PC- parameters of free radicals by the equation (8). The calculations are made for those radicals forming protein and aminoacid molecules (СН, СН2, СН3, NH2, etc), as well as for free radicals being formed during radiolysis and dissociation of water molecules (Н, ОН, Н3О, НО2).
Table 2:Structural PC-parameters calculated via bond energy of electrons.
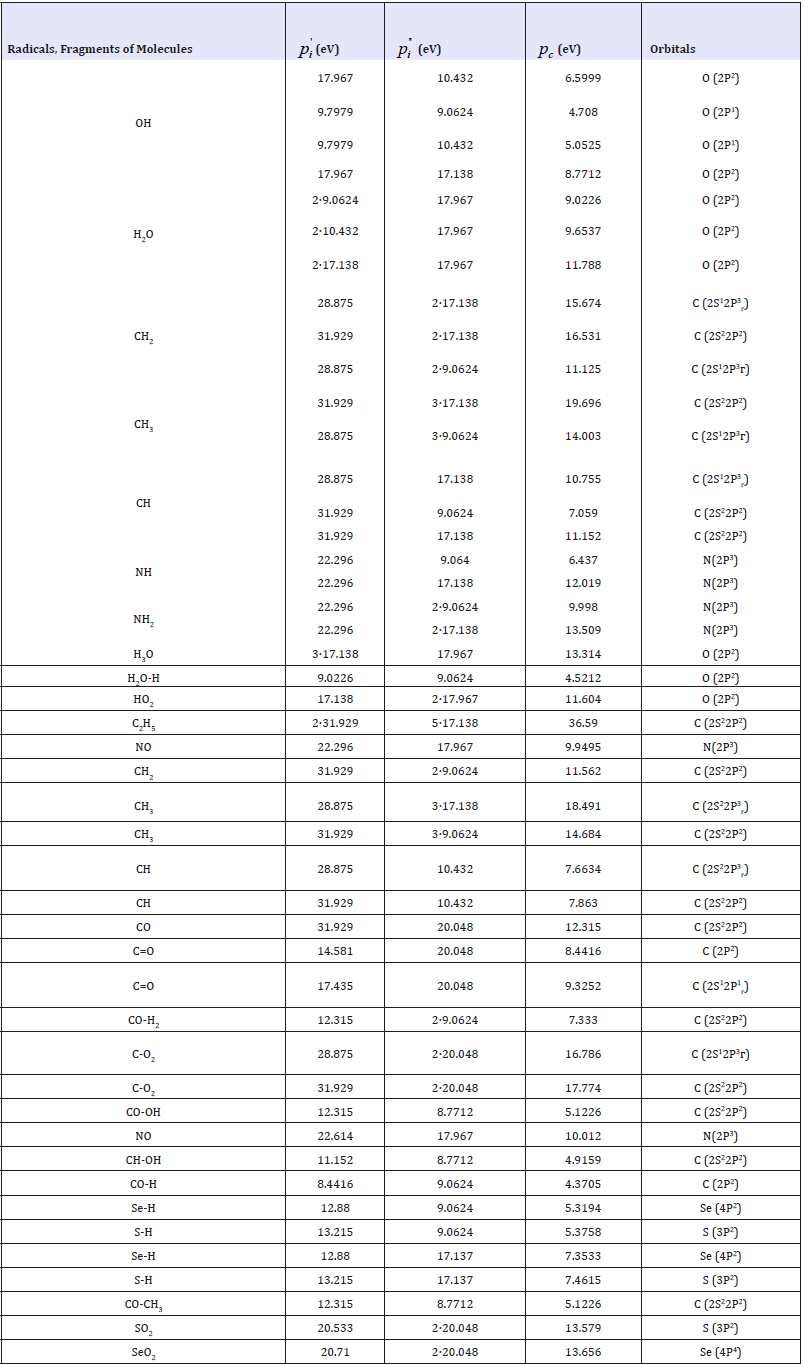
The comparison of PC-parameter values of free radicals obtained with carbon, sulfur, selenium and oxygen atoms was carried out in supposition of paired interactions by all possible variants - based on the equation (9). It should be specifically stressed that here we have the calculations of PE-parameters and structural interactions of practically all possible values of initial dimensional characteristics of atoms. In the norm of stable bonds without external interactions covalent bonds are the most probable in organic molecular structures. The other options of SEI given in Tables 1-3 correspond to such possible structural regrouping when due to some reasons their dimensional characteristics vary from covalent to atomic or even ionic. The results of such calculations of coefficient α and degree of structural interactions (ρ) are given in Table 3, when analyzing it the following conclusions and comparisons can be made:
Table 3:Evaluation of the degree of structural interactions (ρ).
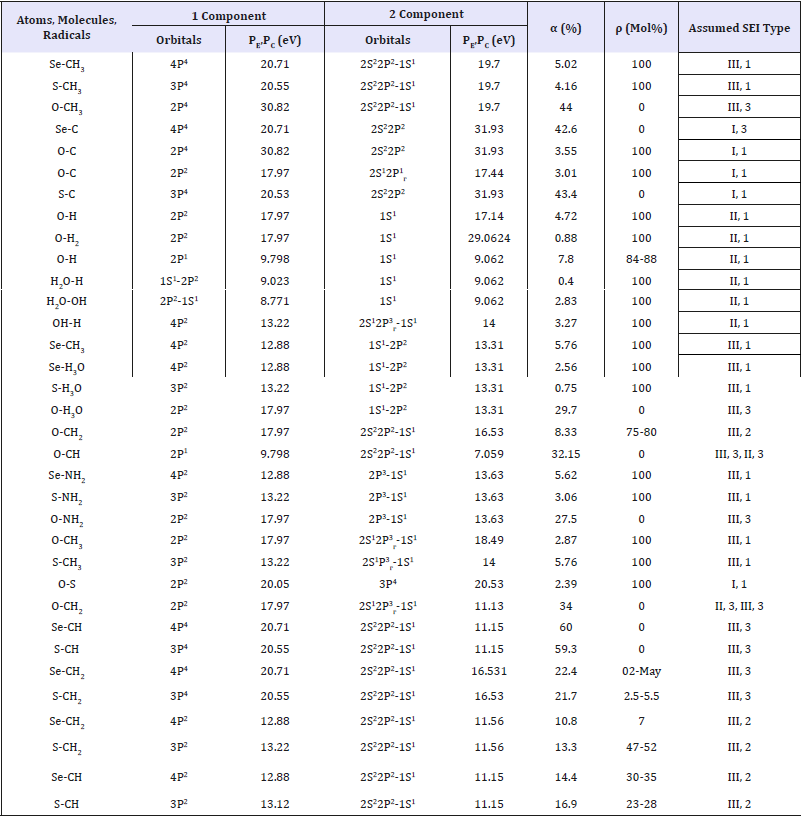
1) Valence orbitals of sulfur and selenium atoms have quite similar values of P-parameters as well as the degrees of structural
interactions (ρ). On the contrary, PE-parameters of oxygen atoms sufficiently differ from such values thus resulting, in many cases, in the opposite results in chemical activity of its atoms.
2) Degree of structural interactions of sulfur and selenium atoms with radicals СН3, NH2, H3O equals 100%. But with radicals СН and СН2 it equals zero or is insignificant - in the range of 0 - 47%. It should be mentioned that structural interactions of the same elements with basic carbon chain of polymeric biomolecules cannot result in their breaking-in since the corresponding values of α for the interactions of Se-C and S-C exceeds 30%, thus ρ=0 in these cases.
Atoms of S and Se can sufficiently structurally influence fragments of СН3 that are frequently located on the ends of hydrocarbon chains or in the form of free radicals. The data given confirm high reactivity of sulfur and selenium atoms as retardants of chain reactions of free radicals as elements “drawing back” unpaired valence electrons of free radicals, but at the same time preserving the basic structure of hydrocarbon chain.
3) Interactions of oxygen atoms result in α > 30% and ρ=0 with structures NH2, H3O and - with radicals СН and СН3 based on С atom (2S22P2). But for radical СН2 on the same base of carbon ρ=75-80 %, and for radical СН3 based on С atom (2S12P3 г) - α=2,87 % and ρ=100 %.
It is also important to add that in contrast to S and Se, atomic structures of oxygen and carbon have great values of PE-parameters and produce SEI at ρ=100 %.
All this means that
a) Degree and character of structural SEI of oxygen are ambiguous and considerably differ from the elements of selenium and sulfur;
b) Oxygen atoms have potential possibilities for decomposing some molecular structures of bio-objects initiating the further freeradical process.
4) Water molecules ( Н2О) produce ρ=100% with free radicals СН2, Н and ОН, this proves the possibility of decreasing the number unpaired electrons in dry bio-objects with their humidity decrease.
In this approach the mechanism of radical Н3О formation
during water dissociation can be apparently explained according
to SEI (Table 3). Hydrogen being released during dissociation by
equation 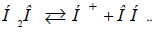 further completely interacts with water
molecules (as they have ρ=100%):
further completely interacts with water
molecules (as they have ρ=100%): 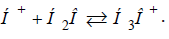
Conclusion
1. Oxygen and its systemic fragments initiate free-radical processes normally producing the rational balance with all forms of active protection of macromolecules from them; in particular, atoms of sulfur and selenium can be applied for that.
2. Spatial-energy characteristics of different valency for sulfur and selenium define the possibility of formation of such structures with these elements that possess multipronged physical and chemical properties from poisons to oxidants.
Methodology of spatial-energy parameter helps not only to explain experimentally determined dependencies of interactions of these elements with free radicals, but also provides practical solution for searching new reagents with given properties.
References
- Golubev AG (2003) Biochemistry of life extending. Success in gerontology 12: 57-76.
- Alexander PA (1959) Nuclear radiation and life.
- Brack C, Bechter-Thuring E, Labuhn M (1977) N-acetylrysteine clows down ageing and increases the life span of Drosophila melanogaster. Cell Mol Life Sci 53(11-12): 960-966.
- Beziepkin VG, Sirota NP, Gaziev AL (1996) The prolongation of survival in mice by dictary antioxidants depends on their age by the start of feeding this diet. Mech Ageing Dev 92(2-3): 227-234.
- Korablev GA (2005) Spatial-energy principles of complex structures formation, netherlands, brill academic publishers and VSP. p. 426.
- Fischer CF (1972) Average-energy of configuration hartree-fock results for the atoms helium to radon. Atomic Data 4: 301-399.
- Waber JT, Cromer DT (1965) Orbital radii of atoms and ions. J Chem Phys 42(12): 4116-4123.
- Clementi E, Raimondi DL (1963) Atomic screening constants from SCF functions. J Chem Phys 38(11): 2686-2689.
- Korablev GA, Zaikov GE (2006) Energy of chemical bond and spatialenergy principles of hybridization of atom orbitalls. J of Applied Polymer Science 101(3): 2101-2107.
- Batsanov SS (2000) Structural chemistry. Facts and dependencies, p. 292.
© 2018 GА Korablev. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






