On the Reological Properties of Human Blood

Blood is a suspension of various solid cells in a liquid plasma, formed from a solution of proteins and minerals. The rheological properties of blood are influenced by individual characteristics of these components as well as factors such as haematocrit, amongst others [1,2]. Whilst plasma itself is a Newtonian fluid, addition of the blood cellular components alters its rheological behaviour towards a shear-thinning non-Newtonian fluid [1,2]. No single rheological model can capture all aspects of this complex fluid, and as such particular aspects can be modelled individually [2,3]. To this end, differing rheological models are applied when predicting flow characteristics depending on area of the circulatory system of interest. For example, blood is often approximated to a Newtonian fluid in arterial flows, though has also been commonly modelled using the Cross [4–7] and Carreau-Yasuda [5–11] models; their constitutive relationships being defined respectively by:

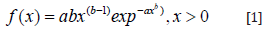
where, Φ(γ˙) is the so-called effective fluid viscocity, μ_o is the low shear viscosity, μ_∞ (∼2-4cP) is the high shear viscosity, λ is the shear time constant and a is a shaping constant termed the Yasuda index. Whilst n∈(0,1) is the power index with values less than unity indicating shear thinning behavoiur, ergo values approaching unity approximate Newtonian behaviour. In this work we have used multivariate optimization routines resident in the SciLab data driven modelling open source software to approximate each of these. The values obtained being compared with the more traditional non- Newtonian constitute relations proposed by Oswald-de Waele [12] & Sisko [13] defined respectfully as:

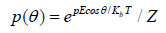
where K is the viscosity consistency and μ_l is a low (non-zero) shear viscosity. To ensure dimensional consistency, each of these are presented here in slightly modified forms to those initially described. As such, they should be more correctly referred to as to as Modified Oswald [12] and Modified Sisko [13] fluids respectfully.

Parameters were approximated for each of the before mentioned rheological models using compiled experimental data from the literature [14-17]. This required a multivariate optimization of the square of the error function, viz:

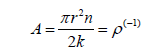
Where μ_m is the mth measurement of the blood viscosity, Φ(γ˙) is constitutive relationship, i.e.: eqn. (1), (2), (3) or (4), and N is the total number of data points. For each of the rheological models we simultaneously fit the free parameter set to experimental data using a variation of the Nelder-Mead optimization algorithm (i.e. fminbnd routine¹) in SciLab open-source data driven modelling code [18]. To preserve structural identification of the Modified Sisko and Carreau-Yasuda fluid models the low shear viscosity terms (μ_l and μ0 respectively) were fixed to 150cP [8,11,19]. The literature maintaining that these terms have no physiological relevance so the calculations that follow are unaffected by this assumption. Cross fluid bounds were used as [1,300], [0.01,1] and [0.01,100] for λ, n and μ_∞ respectively. For the Modified Sisko and Carreau-Yasuda models identical bounds

FOOT NOTE

¹This being resident in the FOSSEE optimization toolbox developed at the University of Bombay:

were used for these parameters as for the Cross fluid. In the case of the latter, an additional bound [0.01,5] was used to represent the Yasuda index (a). In the case of the Oswald-de Waele fluid, the value of K in equation (3) is effectively set (to (150 − 2.3) ≈ 148cP) in order to render a structurally identifiable model with two free parameters. Refined accuracy being obtained (ipso facto verification) via application of an analogous constrained multivariate optimization algorithm. That is, the fmincon routine with initializations set to those previously evaluated from the fminbnd SciLab command. Each of the calculations allowed for 30000 interactions in a time of 16.7 minutes. A convergence tolerance of 10-10 being set for the initial fminbnd calculation with default values being left for the fmincon evaluation which followed.

In most of the cases investigated, the optimization routine reported that either an optimum solution was found or that a solution was obtained to acceptable accuracy. The noteable exception being in the case of the Carreau-Yasuda fluids which initially reported that the maximum number of iterations had been reached. In this case the bounds we altered using successive bisection until a solution to acceptable accuracy was obtained. These values were then used as initialization within the aforementioned SciLab fmincon routine thereby obtaining an optimized solution.

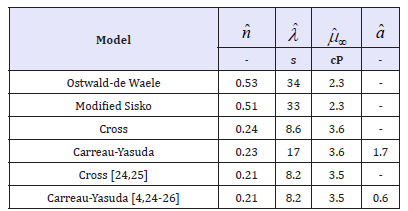
Table 1 compares these calculated parameters with those in the literature [1,3,4,20-23]. Those for Modified Sisko fluid are similar to the Ostwald-de Waele fluid, on the other hand equivalent parameters calculated for the Cross fluid are similar to those of Carreau-Yasuda model. The power index and high shear viscosity values are in good agreement with those quoted in the literature [4,24-26]. Particularly good agreement is demonstrated with respect to values obtained from the Cross and Carreau-Yasuda constitutive relationships and those reported in the literature. This said, analogous values obtained using identical optimization routines for the Modified Ostwald-de Waele and Modified Sisko fluids indicate significantly different values. However, similar values are obtained for the power index and shear time constant when comparing the Modified Sisko and Modified Ostwald-de Waele fluids.

Table 1:Rheological parameters to 2 s.f. obtained from fitting combined existing experimental data shown in Figure 1 to various non-Newtonian models. Experimental data is taken from a variety of sources.

*set value

Discrepancies in the power index calculations are of particular interest from a practical viewpoint. To date the power index has been thought of as a diversion from an idealized Newtonian fluid. The natural assumption being that this quantity is a property of the fluid, hence independent of constitutive relationship, these results certainly suggest that this is not the case. Implying that, at least in the current mathematical forms, the power index is not a property of the fluid.

Figure 1:A log-log plot demonstrating four non-Newtonian constitutive models fitted to collated experimental rheological data for blood adapted from the literature.

Figure 1 demonstrates that the empirical data are well predicted by each of the models to varying degrees; the primary source for these data being Ballyk et al. [20]. Crosses represent experimental blood rheological data collated from several sources i.e. Huang [14], Merrill [15], Cokelet [16] & Skalak [17]. Lines represent rheological models i.e. Ostwald [12], Cross [27], Carreau [28,29], and Modified Sisko [13], fitted to the compiled experimental data.

As expected each of the models converge at higher (imposed) apparent viscosity values. The models predicting the apparent viscosity of the blood at relatively lower shear rates γ ≤ 50s−1 very well. At higher shear rates the model predictions diverge. At the highest measured shear rate 950s−1 the Cross and Carreau-Yasuda models predict higher viscosity values of respectfully 3.77cP and 3.69cP, with the Sisko model predicting a 12% lower viscosity than that the measurement of 3.6cP. Moreover, Figure 1 demonstrates a deficiency with the Ostwald-de Waele model whereby at high shear rates the apparent viscosity is too low in comparison with the empirical data. Indeed, since this model is unbounded at both low and high shear limits unlike other shear-thinning models discussed, its use for evaluating blood is limited to a narrow range of shear rates [30], in this case probably between 1s−1 and 45s−1 (Table1).

A combination of optimization routines has been used to evaluate the constitutive non-Newtonian relationships from compilation of data evident in the literature, via minimization of appropriate least squares error. It was found that the values within each constitutive relationship vary depending on the data set used and non-Newtonian fluid model used. Specifically, this study has shown that:

A. Using these calculated optimized parameters most of the non-Newtonian models describe the empirical data rather well;

B. The Oswald-de Wael model is not suitable for predicating the effective blood viscosity at high shear rates;

C. Due to the similarity of the models the Sisko and Ostwaldde Waele similar constitutive non-Newtonian parameters are apparent; analogous similarities being evident regarding Cross and Carreau fluids;

D. The optimization routine predicts the Carreau-Yasuda and Cross models agree well about analogous parameters as well as values in the literature;

E. The non-Newtonian constitutive parameters (e.g. n,λ and μ_∞and a) may not be properties of blood.

We should also note that there are many more data sets available in the literature. Furthermore, much more advanced technology is available to measure blood viscosity. So, whilst the work herein does raise some interesting observations which have been properly verified, further work is of course required to validate these findings.

1. Oguz KB, Herbert JM (2003) Blood rheology and hemodynamics. Seminars in thrombosis and hemostasis 29: 435-450.
2. Taha Sochi (2013) Non-newtonian rheology in blood circulation.
3. Fuat Y, Mehmet YG, Others (2008) A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea-Australia Rheology Journal 20(4): 197-211.
4. Abraham F, Behr M, Heinkenschloss M (2005) Shape optimization in steady blood flow: A numerical study of non-newtonian effects. Computer Methods in Biomechanics and Biomedical Engineering 8(2): 127-137.
5. Alena J, Jan V (2008) Numerical simulation of non-Newtonian blood flow in bypass models. Proceedings in Applied Mathematics and Mechanics 8(1): 10179-10180.
6. Molla MM, Paul MC (2012) LES of non-Newtonian physiological blood flow in a model of arterial stenosis. Medical Engineering & Physics 34(8): 1079-1087.
7. Mir Golam R, Abdur R, Md. Mamun M (2013) Pulsatile Non newtonian blood flow through a model of arterial stenosis. Procedia Engineering 56: 225-231.
8. Gijsen FJH, Allanic E, De Vosse FNV, Janssen JD (1999) The influence of the non-newtonian properties of blood on the flow in large arteries: unsteady flow in a 90degree curved tube. J Biomech 32(7): 703-713.
9. Johannes VS, George DG, Yiannis SC, Kypriani VS, George EP, et al. (2008) Non-newtonian models for molecular viscosity and wall shear stress in a 3d reconstructed human left coronary artery. Medical engineering & physics 30(1): 9-19.
10. Jie Chen, Xi-YL, Wen W (2006) Non-newtonian effects of blood flow on hemodynamics in distal vascular graft anastomoses. J Biomech 39(11): 1983-1995.
11. Cho YI, Kensey KR (1991) Effects of the non-newtonian viscosity of blood on flows in a diseased arterial vessel. part 1: Steady flows. Biorheology 28(3-4): 241-262.
12. A Dewald (1923) Viscometry and plastometry. J Oil Colour Chem As 6: 33-69.
13. Sisko AW (1958) The flow of lubricating greases. Ind Eng Chem 50(12): 1789-1792.
14. Huang C, King R, Copley A (1973) Rheogoniometric studies of whole human blood shear rates. Biorheology 10(1): 17-22.
15. Edward M, E Gilliland, G Cokelet, H Shin, A Britten, et al. (1963) Rheology of human blood, near and at zero flow: Effects of temperature and haematocrit level. Biophysical J 3: 199-213.
16. Cokelet G, Merrill E, Gilland E, Shin H, Britten A, et al. (1963) The rheology of human blood measurement of near zero and at zero shear rate. Trans Soc Rheol 7: 303-317.
17. Skalak R, Keller S, Secomb T (1981) Mechanics of blood flow. J Biomech Eng 103(2): 102-115.
18. Scilab Enterprises (2012) Scilab: Free and Open Source software for numerical computation. Scilab Enterprises, Orsay, France.
19. Jie Chen, Xi YL (2006) Numerical investigation of the non-Newtonian pulsatile blood flow in a bifurcation model with a non-planar branch. Journal of biomechanics 39(5): 818-832.
20. Ballyk PD, Steinman DA, Ethier CR (1994) Simulation of non-Newtonian blood flow in an end-to-side anastomosis. Biorheology 31(5): 565-586.
21. Barras JP (1969) Blood rheology - general review. Bibliotheca Haematologica 33: 277-297.
22. Jehad Al-Sukhun, Christian L, Unridden A, Heikki P (2007) Microvascular stress analysis. Part I: simulation of microvascular anastomoses using finite element analysis. Br J Oral & Maxillofac Surg 45(2): 130-137.
23. Stephane A, Jonathan MH, Rhodri C (2009) In vivo measurements of blood viscosity and wall stiffness in the carotid using PC-MRI. European Journal of Computational Mechanics 18(1): 9-20.
24. Leuprecht, Perktold K (2001) Computer simulation of non-newtonian effects on blood flow in large arteries. Computer methods in biomechanics and biomedical engineering 4(2): 149-163.
25. SHU Chien (1975) Biophysical behavior of red cells in suspensions. In: Douglas MacN (Edr.), The Red Blood Cell (Second Edition), pp. 1031- 1133.
26. Joshua B, James MB, Simon G (2007) Analysis of the Casson and Carreau- Yasuda non-Newtonian blood models in steady and oscillatory flows using the lattice Boltzmann method. Physics of Fluids 19: 3103.
27. Malcolm MC (1965) Rheology of non-newtonian fluids: A new flow equation for pseudoplastic systems. Journal of Colloid Science 20(5): 417-437.
28. Pierre JC (1972) Rheological equations from molecular network theories. Transactions of the Society of Rheology 16(1): 99-127.
29. Kenji Y (1979) Investigation of the analogies between viscometric and linear viscoelastic properties of polystyrene fluids. Thesis, Massachusetts Institute of Technology.
30. Robertson M, Sequeira A, Owens RG (2009) Rheological models for blood. In: Formaggia L, Alfio Q, Veneziani A (Eds.), Cardiovascular Mathematics: Modeling and simulation of the circulatory system. Pp. 211-241.