Ffssa-Fiege Fiat Shamir Security Algorithm an Efficient Security Algorithm for Body Area Wireless Sensor Networks

WSN's are generally deployed for collecting data from unattended or hostile environment. Several application specific sensor network cryptography algorithms have been proposed in research. however wsn's has many constrictions, including low computation capability, less memory, limited energy resourses, vulnerability to physical capture ,which enforce unique security challenges needs to make a lot of improvements. In this paper presents a novel cryptography algorithm for wireless sensor network security, which presents a generic transformation from weak secure symmetric and asymmetric scheme to a hybrid encryption scheme. A revised Feige-Fiat-Shamir ZKP scheme for the Wireless sensor Networks (WSNs) that reduces the execution dynamics in the scheme and increases the trust of the Verifier and prover, and makes the authentication process faster and more efficient.

Keywords: WSN; Forward security; Canonical ID scheme; FS transform; Digital signature; Forger algorithm

Wireless sensor nodes are resource constrained. They have limited processing capability, storage capacity, and communication bandwidth. The security design of WSNs must consider the hardware limitations of the sensor nodes. The Constrains of WSN nodes are energy, computation, memory, and transmission range.

In sensor nodes energy consumption is needed for sensor transducer, communication among sensor nodes, microprocessor computation [1]. The embedded processors in sensor nodes are usually not as potent as those in nodes of a wired network. So that, cannot be used for complicated cryptographic algorithms in wireless sensor networks. In sensor node normally flash memory and RAM are used. For storing downloaded application code Flash memory is used, RAM is used for storing intermediate computations, application programs, and sensor data. There is generally not sufficient space to run complex algorithms after loading OS and application. For example, Tiny OS uses 3500 bytes of data consumes for instruction memory, and has only 4500 bytes for security and applications [2]. This makes use of present security algorithms almost impractical [3].

A WSN is normally composed of hundreds of sensor nodes. These sensor nodes are deployed densely in a field and have the capability to gathering data to back to a base station. A wireless sensor node consists of a sensing unit, a processing unit, a transceiver unit, and a power unit [4] (Figure 1). Sensing units contain the subunits of sensors and analog-to-digital converters. The sensors sense the phenomenon and convert the analog signal into digital signal. The processing unit encompasses a small storage unit, which makes the sensor node to collaborate with other nodes. A transceiver unit associates the node to the network. A power unit may be a single battery or may be sustained by power scavenging devices (e.g., solar cells).

Figure 1: A WSN is normally composed of hundreds of sensor nodes.

The sensor nodes uses protocol stacks [4] that contain physical, data link, network, transport, and application layers. The physical layer is liable for frequency selection, carrier frequency generation, signal deflection, modulation, and data encryption. Data link layer is responsible for the multiplexing of data streams, error control, data frame detection, and medium access. Network layer is liable for stating the assignment of addresses and how packets are forwarded. Transport layer is responsible for identifying how the consistent transport of packets will take place. Application layer is responsible for reporting receipt of the data to the individual sensor nodes and all contacts with the end user.

Attacks

Sensor nodes are prone to many kinds of attacks. For a large- scale sensor network, it is not practically possible to monitor and defend each single sensor from physical or logical attack. Attacks on sensor networks can be classified [5] into attacks on (layer wise) physical, link (medium access control), network, transportation, and application layers. Based on the capability of attacker, Attacks can also be classified in to, sensor level and laptop-level. A powerful laptop-level opponent can do far more harm to a network than a malicious sensor node, subsequently it has enhanced power supply, as well as greater computation and communication capabilities than a sensor node.

Attacks can furthermore be classified into outside and inside attacks. In sensor networks most cryptographic materials, an outside attacker has no access, whereas an inside attacker may have partial key materials and the trust of other sensor nodes. Inside attacks are much harder to identify and protect against. Reviewed the typical attacks on sensor networks [6] and the possible defense techniques by the corresponding network layer, and the available protection techniques:

a) Jamming (physical layer): spread-spectrum, lower duty cycle

b) Tampering (physical layer): effective key management schemes, tamper-proofing

C ) Collision (link layer): error correcting code

d) Exhaustion (link layer): rate limitation

e) Manipulating routing information (network layer): authentication, encryption

f) Selective forwarding attack (network layer) redundancy, probing

g) Sybil attack (network layer): authentication.

Cryptography [7] is the basic encryption scheme used in security applications. Symmetric key cryptography uses the same key for encryption and decryption. Another type of encryption method is asymmetric or public key cryptography which uses different keys to encrypt and decrypt. A asymmetric key cryptography (e.g., the RSA signature algorithm) requires more computation resources than symmetric key cryptography (e.g., the AES block cipher), Symmetric key cryptography is difficult for key deployment and management. Cryptographic methods used in WSNs should encounter these limitations related to sensor nodes and be estimated before choosing. In this section, we focus on new algorithm which is going to apply. The big advantage of this algorithm is that it simplifies key management.

In wireless sensor networks, have to design crypto graphical algorithm to rectify the constraints mentioned above, The existing algorithms problems are related to size of algorithm's code, the size and structure of internal data and parameters, execution dynamics, and the usage of system resources. Instead of modifying security requirements, or using smaller, but weaker algorithms, or eventually inventing new cryptographic algorithms [8], in order to solve problems caused by memory limitations, Developed an innovative approach for usage of data memory in sensor nodes. The kernel of the method is providing minimal conditions on the identification scheme to strengthen the security of the signature scheme in the random oracle model. Both in the usual and in the forward-secure cases. Specifically, it is shown that the signature scheme (forward-secure) is immune to chosen-message attacks in the random oracle model. It also works (forward-secure) against impersonation under passive (i.e., eavesdropping) attacks.

Fiege-fiat-shamir algorithm

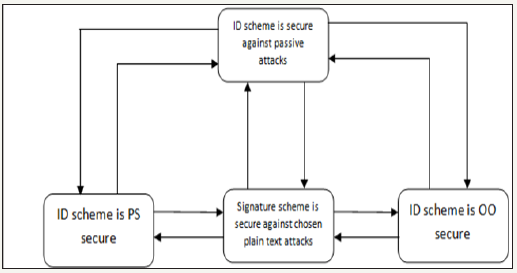
The improvement on Fiat-Shamir method contains canonical ID scheme, FS transform, Digital signature scheme, forger algorithm, forward security. Figure 2 shows the three assumptions made on non-trivial identification schemes for the purpose of proving security of the corresponding FS-transform based signature scheme: [9] PS-security , OO-security , and the assumption of security against imitation under passive attacks. As the figure indicates, all the three serve to prove security of the signature scheme in the random oracle model.

Figure 2:F-F-S security scheme.

Canonical identification protocol

We use the term canonical to describe a three-move protocol in which the verifier's move contains of picking and sending a random string of some length, and the verifier's final decision is a deterministic function of the exchange and the public key (Algorithm). [10] The specification of a canonical identification scheme will take the form ID = (K, P,V , c) where K is the key generation algorithm, taking input a security parameter k ϵ N and returning a public and secret key pair (pk, sk); P is the prover algorithm taking input sk and the current conversation prefix to return the next message to send to the verifier; c is a function of k indicating the length of the verifier's challenge; V is a deterministic algorithm taking pk and a complete conversation transcript to return a boolean decision Dec on whether or not to accept (Figure 3).

Figure 3:A canonical identification protocol.

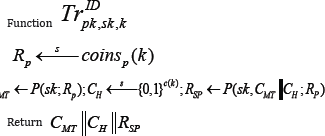
Security of an identification scheme under passive attacks

Let I be an impersonator and Let ID= (K,P,Vc) be a canonical identification scheme , be its state , and k be the security parameter .Define I as

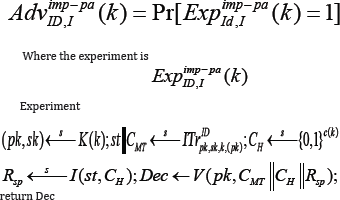
We say that ID is polynomially -secure against impersonation under passive attacks if is negligible of r every probabilistic poly (k)-time impersonator I .

Digital signature pattern

The specification of a digital signature scheme [11] has the form DS = (K,S,Vf,c) where K is the key generation algorithm, taking input a security parameter k ϵ N and returning a public and secret key pair (pk,sk ); S is the signing algorithm taking input sk and a message M ϵ {0, 1} to be signed and returning a signature; Vf is the verification algorithm taking input pk, a message M and a candidate signature a for M and repaying a boolean decision. The signing and verifying algorithms have oracle admittance to a function H: {0, 1}*→ {0, 1}c(k) (which in the random oracle model will be a random function) so that c in the scheme description is a function of k whose value is the output-length of the hash function being used.

Let DS = (K,S,V,c) be a digital signature scheme, let F be a factor and k the security parameter.

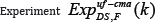
Figure 4:

If M was previously queried to S^H_sk (*) then return 0 Else return Dec

Define F as

DS is polynomially-secure against chosen message attacks if 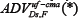is negligible for every probabilistic poly (k)-time forger F.

Fiat shamir transform

Let ID = (K,P,V,c) be a canonical identification scheme(12), and let s: N→N be a function which we call the seed length. We subordinate to these a digital signature scheme DS = (K,S,Vf,c). It has the same key generation algorithm as the identification scheme, and the output length of the hash function equals the challenge length of the identification scheme. The signing and verifying algorithms are defined below Figure 4.

Figure 5

Figure 6:

It runs the impersonator I as a subroutine, answering the latter's transcript oracle queries via its signing oracle. When I outputs a commitment, F increments M, picks a random seed R, and defines the verifier's challenge via a hash query. It provides this to I, obtains a response Rsp, and uses the latter in its forgery. The messages used in the algorithm [12] are generated by incrementing a counter and interpreting its value as a string. It can be represented as follows;

Algorithm:

(Figure 5)

Forward security (for passive attacks)

[13] Let FID = (K, P, Vid, Up, c, T) be a canonical key-evolving identification scheme, and let I be an impersonator and k be the security parameter. The algorithm represented as follows (Figure 6) ; All these Fiege-Fiat-Shamir algorithm serve to prove security of the signature scheme in the random oracle model.

Security is precarious for many sensor networks. Due to the limited capabilities of sensor nodes, providing security and privacy to a sensor network is a challenging task. In this article, This paper encapsulate typical attacks on sensor networks and surveyed the literatures on several important security issues relevant to the sensor networks, including cryptography. Many security issues arise in wireless sensor networks due to the above said attacks. This F-F-S cryptographical algorithm avoids most of the attacks. The FFS algorithm is more secure, and meet all security requirements and rectifies the wsn constraints.

1. IF Akyildiz (2002) A survey on sensor set works. IEEE Commun Mag 40(8): 102-114.
2. J Hill, Robert S, Alec W, Hollar S, David C, et al. (2000) System architecture directions for networked sensors, asplosix: proc. 9^th int'l conf architectural support for programming languages and operating systems. ACM Press, NewYork, USA, pp. 93-104.
3. Perriget A, Robert S, JD Tygar, Victor W, David EC, et al. (2002) SPINS: Security protocols for sensor networks. Wireless Networks 8(5): 521534.
4. GJ Pottie, WJ Kaiser (2000) Wireless integrated network sensors. Commun ACM 43(5): 51-58.
5. Chan H, Perrig A (2003) Security and privacy in sensor networks. Computer 36(10): 103-105.
6. Xiaojang Du, Hsiao-hwa Chen (2008) security in wireless sensor networks. IEEE wireless communications 15(4): 60-61.
7. Xiangqian C (2009) sensor network security-a survey. IEEE communications surveys and tutorials 11(2).
8. Djenouri D, Khelladi L, Badache N (2005) A Survey on security issues in mobile ad hoc and sensor networks. IEEE Commun Surveys and Tutorials 7(4): 2-28.
9. Pointcheval D, Jacques S (2000) Security arguments for digital signatures and blind signatures. Journal of Cryptology 13(3): 361-396.
10. M Abdalla (2002) From identification to signatures via the fiat Shamir transform: minimizing assumption for security and forward security. Advances in cryptology-EUROCRYPT 2332: 418-433.
11. Goldwasser S, Silvio M, Rivest RL (1988) A digital signature scheme secure against adaptive chosen-message attacks. SIAM Journal on Computing 17(2): 281-308.
12. Benny C, Goldreich O (1985) Unbiased bits from sources of weak randomness and probabilistic communication complexity. In 26^th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Portland, pp. 429-442.
13. Mihir B, Miner KS (1999) A forward-secure digital signature scheme. In: Michael J Wiener [Ed.], Advances in Cryptology - CRYPTO'99. 1666 of Lecture Notes in Computer Science, Germany, pp. 431-448.