- Submissions

Full Text
Research in Medical & Engineering Sciences
Ising Model in One-Dimensionalon Directed Small- World Networks
FWS Lima*
Departamento de Física, Universidade Federal do Piauí, Brazil
*Corresponding author: FWS Lima, Dietrich Stauffer Computational Physics Lab, Departamento de Física, Universidade Federal do Piauí, 64049-550, Teresina-PI, Brazil
Submission: December 07, 2017; Published: December 21,2017

ISSN: 2576-8816Volume3 Issue1
Abstract
We investigate the critical properties of the Ising model one-dimensional (1D) on directed small-world networks. This Ising mode is studied by applying the Monte Carlo method. We calculate the critical points, as well as the critical exponents ratio, y/v, p/v and 1/v. We find that this systems present identical exponents to the Ising and Majority-vote model on Solomon networks (1D) and are of different universality class as the regular twodimensional ferromagnetic model. Our results are in agreement with the Grinstein criterion for models with up and down symmetry on regular lattices.
Introduction
It is known from the literature that the Ising models in one-dimension (1D) [1] there is no phase transistion at finite temperature T, while two-dimension (2D) presents a continuous phase transition. Pekalski [2] studied the Ising model on a small- world network (SW) constructed from a ring lattice. In the presence of a finite fraction of additional long-range interactions, the model presents a phase transistion a finite temperature.
However, the exponent p=0 was found to be very small, p= 0.00001, in contrast to the previous studies suggesting the mean- field nature of the transistion [3,4]. Hong et al. [5] presented results of extensive Monte Carlo simulations of the same model as that in Pekalski [1] , which reveal that the phase transistion is described by the mean-field exponents α=0, β=0.5, γ=1, and v=2.
In this paper we consider the Ising model in 1D ( or ring lattice ) directed small-world networks (DSW) and perform an extensive computer simulation study of the Ising model. We applied finite- size scaling (FSS) techniques to extract the exponents and the "renormalized charges" U40 “. Monte Carlo simulations of this system was performed using the spin-flip heat bath algorithm to update the spins. Here, there is a second-order phase transition for 0 < p♦1, where p is the rewiring probability. In addition, the calculated critical exponents for p do not belong to the same universality class as the regular two-dimensional ferromagnetic model.
Small-World Networks
In 1967, Jeffrey and Stanley Milgram conducted an experiment with the objective of to have Omaha residents send letters to the residents of the city of Boston, either directly or through acquaintances. Initially they believed that the cards would reach their destination by approximately 100 people. The results showed that of the 160 letters sent, 42 arrived at the destination and that these letters passed on average by five to six intermediate persons [4]. Like this experiment they showed that people would be living in a small world.
In 2003 Ducan JW & Steven [4] proposed a small-world network model with the goal of forming few connections between each individual. In this model the population is distributed in regular one-dimensional networks in which each individual contact the other individuals in the network through re-connections made from the value of the probability p.
The small-world network in one-dimension is built from a regular network with two closest neighbors, connected to N nodes and C neighbors. In this network each node is randomly reconnected with n edges with probability p. When p=0 for the network it is regular (received no long-range connection), but for 0 <p <1 the network is small world (short-range links) and p=1 random network (long-range connections), as shown in Figure 1.
Model and Simulations

where T is the temperature, KB is the Boltzmann constant, and Ej is the energy of the St obtained of

where the sum runs over all neighbours k of i with k = 3 on SNs and the variables Si assume values. In the above equation J is the exchange coupling. comprising a number L=1000, 2000, 4000, 8000,and 16000 of sites. For each system size quenched averages over the connectivity disorder are approximated by averaging over independent realizations. For each simulation we have started with a uniform configuration of spins. We ran Monte Carlo steps (MCS) per spin with 2x105 configurations discarded for thermalization using the "perfect” random-number generator [6]. We do not see any significant change by increasing the number of replicas (R) (for example R=50) and MCS. So, we keep these values constant once they seem to give reasonable results for all simulations.
Results and Discussions
Figure 1: The three networks with the same numbers of nodes, the same number of links and the same placement of nodes. (a). Regular network (ring-lattice), ( b) Small- world network (the Watts-Strogatz Model), and (c) Random network.

Figure 2: Plot of the logarithm of the magnetization (a) and susceptibility X (b) at T as a function of the logarithm of L. ln '\Tc (L) - Tc ] Plot of (c) and In x r... (d) as a function of the logarithm of L.

The magnetization per spin, 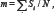 , were measured. We magnetization, the susceptibility, and the fourth-order magnetic can derive from the magnetization measurements the average cumulant,
, were measured. We magnetization, the susceptibility, and the fourth-order magnetic can derive from the magnetization measurements the average cumulant,

in the above equations <...> stands for thermodynamic averages and ... [...]av for averages over different realizations.
In order to calculate the exponents of these models, we apply finite-size scaling (FSS) theory. We then expect, for large system sizes, an asymptotic FSS behavior of the form

where â and ã are the usual critical exponents, and f (x) are FSS functions with

being the scaling variable. The dots in the brackets [1+...] indicate corrections-to-scaling terms. We calculated the error bars from the fluctuations among the different realizations. Therefore, from the size dependence of m and ÷ we obtain the exponents ratios â / i and ã/ i, respectively. The susceptibility at its maximum also scales as Lã/i .Moreover, the value of T° =Tc (L) for which ÷ has a maximum scales with the lattice size as Tc (L) = Tc+ bL-i/ . In this way, Eq. 9 may be used to get 1/ i [7,8].
In the Figure 2b, we plot logarithm of the susceptibility χ at Tc versus lnL. Of the eq. (7), we obtain the exponents ratio γ/vTc = 0.65(1),0.56(4), and 0.56(3) for p=0.1,0.5 and 0.9, respectively.
In the Figure 2c, we plot the log-log of \Tc (L)-Tc ] versus L and 8. Janke W, Villanova R (1995) Phys Lett A 209: 179.the eq. (8), we obtain the exponents ratio 1/v=0.52(3),0.53(2) and 0.53(3) for p=0.1,0.5 and 0.9, respectively.
The Figure 2d display logarithm of the susceptibility χ at Tmax versus logarithm of L. The values of the exponents ratio are ã/ fmax = 0.65 (1) ,0.54 (2) and 0.54(3) again for p=0.1,0.5 and 0.9, respectively.
Conclusion
In the present work, we have shown that, by considering the ferromagnetic Ising model in one-dimension on DSW networks there is a continuous phase transition. Our results are different from Ising model in one-dimension on a chain that no presents phase transition. We believe this critical behavior is due to the short and long links present in this DSW networks.
Acknowledgement
The author would like to thank the Brazilian agencies CNPq and Capes.
References
- Lenz W, Phys Z (1921) 21: 613. Ising E, Phys Z (1925) 31: 235.
- Pekalski (2001) Phys Rev E 64, 057104.
- Herrero P (2002) Ising model in small-world networks. Phys Rev E 65: 066110.
- Watts J (1999) Small worlds, the dynamics of networks between order and randomness. Princeton University Press, Princeton, USA.
- Hong H, Beom JK, Choi MY (2002) Rapid communications. Phys Rev E 66(1): 018101.
- L'Ecuyer P (1988) Efficient and portable combined random number generators. Commun ACM 31(6): 742-751.
- Wang JS, Lebowitz JL (1988) Phase transitions and universality in nonequilibrium steady states of stochastic Ising models. Journal of Statistical Physics 51(5-6): 893-906.
- Janke W, Villanova R (1995) Phys Lett A 209: 179.
© 2017 FWS Lima. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






