Modeling of Cr³⁺ Doped β-Ga_{2O3 Single Crystals}

Electron Paramagnetic Resonance (EPR) is a powerful tool for investigating the local site symmetry and Zero Field Splitting (ZFS) of impurity ions in host crystals [1,2]. Superposition Model (SPM) [3-5] is frequently employed to find theoretically the Crystal Field (CF) parameters and Zero Field Splitting (ZFS) parameters.

β-Ga_{2O3, gallium oxide, is an insulator having a band gap of 4.8eV [6]. When synthesized under reducing conditions, it becomes an n-type semiconductor [7]. Doping yields variation in the conductivity of both the p and n types. These materials have potential applications in optoelectronics These are also used as insulating or conductive window material or substrates [8]. As the above material is stable at high temperatures, it has been widely studied for application as a gas sensor [9]. The electrical conductivity of Ga2O3 at large temperatures is changed in the presence of oxidizing or reducing gases. β-Ga2O3 has become a good material for optoelectronic devices in the deep ultraviolet region [10]. Gallium oxide crystal doped with trivalent transition ions is of importance in microwave, optical maser and exchange interaction between substitutional ions studies [11]. Introduced impurities giving microscopic structural change affect the optical properties of the crystal based on location of the impurities. The Cr³⁺ion is a very important probe for obtaining information on β-Ga2O3 crystal.}

The EPR study of Cr³⁺ doped β-Ga_{2O3 has been reported [12]. The EPR spectra of Cr³⁺ ions in β-Ga2O3 single crystals were recorded on an X-band spectrometer at room temperature. These spectra in the three mutually perpendicular planes were analyzed employing an effective spin Hamiltonian. The spectroscopic splitting factor g and the Zero Field Splitting (ZFS) parameters of Cr³⁺ ions were obtained for the octahedral substitutional sites in β-Ga2O3 single crystal. The actual local site symmetry of Cr³⁺ ions in the crystal was also investigated.}

The laboratory axes (x, y, z) are chosen to be along the crystallographic axes (a, b, c*). The symmetry adopted axes (magnetic axes) are labeled (X, Y, Z). The principal Y axis of g and D tensors of Cr³⁺ ions is found parallel to the crystallographic b axis (monoclinic C2 axis). The principal axes of g and D tensors in the plane normal to the C2 axis do not coincide. If an external magnetic field is applied in a plane not containing the C2 axis, the resonance fields are asymmetric about the extrema [12]. These principal directions and the asymmetry show that the local site symmetry of Cr³⁺ ions in β-Ga_{2O3 crystal is monoclinic. In the principal magnetic axis system, the parameters g, D and E were obtained using EPR-NMR program. There are two chemically distinguishable Ga3+ sites in the unit cell: Ga13+ ions coordinated with four oxygens and Ga23+ ions coordinated with six oxygens [13]. The Cr³⁺ ion EPR spectrum shows a single set of three lines indicating Cr³⁺ ions to be located at only one site. Cr³⁺ ions with an ionic radius 0.0615nm for the six-fold coordination prefer the octahedrally coordinated Ga23+ site (ionic radius 0.062nm) [12].}

The present investigation presents the Superposition Model (SPM) of the CF parameters and the ZFS parameters for Cr³⁺ ions in β-Ga_{2O3 crystal. The aim is to obtain the ZFS parameters, the CF parameters and the distortion in the lattice for the Cr³⁺ ions in β-Ga2O3 at octahedral sites. The optical energy band positions for Cr³⁺ ions in β-Ga2O3 are computed using CF parameters and Crystal Field Analysis (CFA) program. The CF parameters and ZFS parameters evaluated may be useful in future investigations for scientific and industrial applications of such crystals.}

Crystal structure

The crystal structure of β-Ga_{2O3 is monoclinic with space group C2/m [14]. The lattice parameters are a =1.2214nm, b=0.30371nm, c=0.57981nm, β=103.83° and Z=4. Two chemically distinct cation sites are coordinated with oxygens either tetrahedrally or octahedrally. The structure shows double chains of GaO6 octahedra (Ga2) parallel to the b axis, which are connected by GaO4 tetrahedra (Ga1). The crystal structure of β-Ga2O3 with symmetry adopted axis system (SAAS) is given in Figure 1.}

Figure 1:Crystal structure of β-Ga_{2O3 with symmetry adopted axis system (SAAS).}

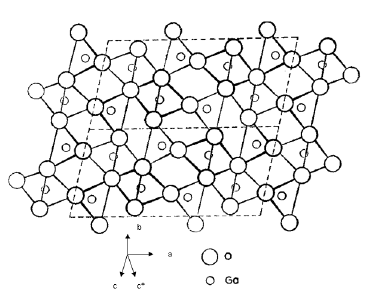
The Symmetry Adopted Axes (SAA) (local site symmetry axes) are the mutually perpendicular directions of metal-ligand bonds. The Z axis of SAAS is along the metal-ligand bond Ga2-O1 (crystal c*-axis) and the two other axes (X,Y) are perpendicular to the Z axes (in the ab plane) for center I (Figure 1). This shows that Cr³⁺ substitutes for Ga²³⁺ in the crystal of β-Ga_{2O3 with approximately orthorhombic symmetry. The ionic radius of Cr³⁺ ion (0.0615nm) [15] is slightly smaller than the ionic radius of Ga²³⁺ (0.062nm) suggesting Cr³⁺ ion to sit at the location of Ga²³⁺ with certain distortion.}

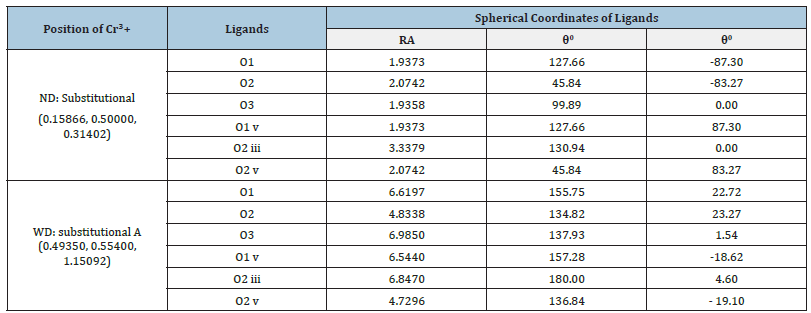
The Cr³⁺ ion position and spherical polar coordinates of the ligands in β-Ga_{2O3 [14] for center I are given in Table 1. These data are used for ZFS and CF calculations for Cr³⁺ ion in β-Ga2O3.}

Table 1:Fractional coordinates of Cr³⁺ ion (center I) and spherical co-ordinates (R, θ, ф) of ligands in β-Ga₂O₃ single crystal.

Calculations of zero field splitting parameters

The spin Hamiltonian [16-18] used to find the energy levels of Cr³⁺ ions in crystals is:

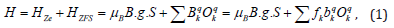
Where g, μB and B are the spectroscopic splitting factor, Bohr magneton and static magnetic field, respectively. S represents the effective spin operator and O^q_k(S_x,S_y,S_z) are the Extended Stevens Operators (ESO) [19,20]; B^q_k and b^q_k are the ZFS parameters, ƒk=1/3 and 1/60 are the scaling factors for k = 2 and 4, respectively. The ZFS terms in (1) for Cr³⁺ ion (S=3/2) at orthorhombic symmetry sites are given as [21,22]:

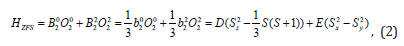
The conventional orthorhombic ZFS parameters D, E and B^q_k are related as follows:

The ZFS parameters (in ESO notation) for any symmetry employing SPM [21,22] are obtained as:

Where (Ri, θI, ϕi) are the spherical polar coordinates of i-th ligand. The intrinsic parameters b_k provide the strength of the k-th rank ZFS contribution from a ligand at the distance Ri and the coordination factors K^q_k give the geometrical information. K^q_k for k = 1 to 6 in the ESO notation [23] are presented in Appendix A1 of [24].

Eq. (4) provides conventional ZFS parameters, D and E, in terms of the intrinsic parameters b_k , the power-law exponents tk, and the reference distance R0, as [24,25-27]:

Cr³⁺ ion in β-Ga₂O₃ may be supposed to substitute at the Ga₂₃₊ ion site, and the interstitial site with similar ligand arrangement. The local symmetry at Cr³⁺ ion site is assumed to be approximately orthorhombic. In octahedral coordination of Cr³⁺ ion in LiNbO3 having Cr³⁺-O2- bond, 2 0 b (R )=2.34cm-1 and t2=-0.12 [28] were used to obtain b⁰₂ and b²₂ . Because Cr³⁺ ion in β-Ga₂O₃ has distorted octahedral coordination (Figure 1) with oxygen as ligands, the b^q_k in the present investigation are determined using b₂ (R₀) =2.34cm- 1 and t₂=-1.96 for the center I.

The Cr³⁺ ion position and spherical coordinates of ligands shown in Table 1 are used for calculation. The conventional ZFS parameters, D and E of Cr³⁺ ion in β-Ga₂O₃ single crystal are evaluated employing Eq. (5). The reference distance R0=0.200nm was taken for the calculation of ZFS parameters [29], and the values are: |D|=88.7×10^-4cm^-1 and |E|=25.7×10^-4 cm^-1 for center I. The ratio b²₂/b⁰₂ should be within the range (0, 1) for orthorhombic symmetry [30]. In the present computation, the ratio 2 0 |b²₂|/|⁰₂| =0.870 and |E| / |D| = 0.290 for center I. It is seen that the value of |D| and |E| do not agree with the experimental values though |b²₂|/|b⁰₂| is in the specified range [30]. Hence, with above t2 and reference distance R0, the ZFS parameters |D| and |E| are calculated for Cr³⁺ at the Ga₂₃₊ site with distortion having position Ga₂₃₊ (0.49350, 0.55400, 1.15092) for center I. The conventional ZFS parameters found now are |D|=5385.2×10^{-4cm-1, |E|=1288.2×10- 4cm-1 for center I, which are in good match with the experimental ones. The ratio |b2₂|/|b0₂| =0.717 and |E| / |D| = 0.239 for center I are in the specified range [30]. Further, with above t2 and reference distance R0, the ZFS parameters |D| and |E| are computed for Cr3+ at the interstitial site but the values found in this case are inconsistent with the experimental values. Hence, these data are not shown here.}

The calculated and experimental ZFS parameters for Cr³⁺ ion in β-Ga₂O₃ are given in Table 2. It is seen from Table 2 that the ZFS parameters |D| and |E| are in good match with the experimental ones [12] when the distortion is introduced into calculation.

Table 2:Calculated and experimental ZFS parameters of Cr³⁺ doped β-Ga₂O₃ single crystal for center I along with reference distance.

ND = No distortion, WD = With distortion, e = experimental.

Calculations of crystal field parameters

The CF energy levels of transition ions in crystals [31-34] using Wybourne operators [15,16,35] are given by:

Where ℋ CF is CF Hamiltonian. The CF parameters in (6) for a metal-ligand complex are determined using SPM [21,22] as:

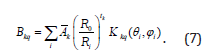
Where R0 is the reference distance; Ri, θi, φi are the spherical polar coordinates of the ith ligand and Kkq are the coordination factors [31]. To obtain B_kq (k=2, 4; q=0, 2, 4); A = 40, 400cm^-1, t₂ =1.3, 4 A =11, 700cm^-1 and t4 = 3.4 are used [31]. The calculated B_kq parameters are presented in Table 3. The ratio B²₂/B⁰₂ = 0.255 for center I, which indicates that B_kq parameters are standardized [30]. Taking B_kq parameters given in Table 3 and CFA program [32,33], the CF energy levels of Cr³⁺ ion in β -Ga2O3 single crystals are calculated by diagonalizing the complete Hamiltonian. The calculated energy values are given in Table 4. The calculated energy values are compared with the experimental energy values for Cr³⁺: β-Ga₂O₃ [36]. From Table 4, it is noted that the theoretical and experimental band positions are in reasonable match. Thus the theoretical study of Cr³⁺ ions at Ga₂₃₊ sites in β-Ga₂O₃ supports the experimental one [12,36].

Table 3:B_kq parameters of Cr³⁺ doped β-Ga₂O₃ single crystal for center I with distortion.

WD = With distortion.

Table 4:Experimental and calculated energy band positions (centers I) of Cr³⁺ doped β-Ga₂O₃ single crystal.

(Racah parameters A, B and C, spin-orbit coupling constant and Trees correction are 0, 726.3, 2905.2 (= 4B), 276 and 70cm^-1, respectively)

The optical absorption/excitation spectra of Cr³⁺-activated phosphors have been explained with the help of Franck-Condon analysis with the Configurational-Coordinate (CC) model [37]. The different excited state-ground state transitions in Cr³⁺ are because of the strong coupling with the lattice vibrations (CC model) [37]. The CC model has not been employed and hence there is difference between excited-state peak energies found here and Zero-Phonon Line (ZPL) energies discussed in [37,38]. The Cr³⁺-activated oxide phosphors are classified into two groups: O-Cr-A and O-Cr-B [38]. Phosphors of O-Cr-A type have an energy inequality relation of E(2Eg)ZPL < E(4T2g)ZPL, giving a series of the sharp emission peaks by the 2Eg → 4A2g transitions. Phosphors of O-Cr-B type have an energy inequality relation of E(4T2g) ZPL < E(2Eg) ZPL, giving a broad emission band due to the 4T2g → 4A2g transitions. β-Ga₂O₃: Cr³⁺ comes under O-Cr-B type phosphors [38].

The Zero-Field Splitting (ZFS) parameters and Crystal Field (CF) parameters for Cr³⁺ ions in β -Ga2O3 single crystals are calculated with the help of Superposition Model (SPM). Cr³⁺ ions in β -Ga2O3 crystal at Ga₂₃₊ ion sites, interstitial site and distortion models are considered for calculation. The calculated conventional ZFS parameters for Cr³⁺ ion at Ga₂₃₊ sites in β-Ga₂O₃ single crystal provide good agreement with the experimental values when distortion is included in the calculation. It is noted that the Cr³⁺ ions substitute at Ga₂₃₊ ion sites in β-Ga₂O₃ lattice. The CF energy values for Cr³⁺ ions at Ga₂₃₊ sites computed using CFA package and CF parameters are in reasonable match with the experimental ones. Thus, the theoretical results support the experimental study.

Modeling procedure employed in this investigation may be useful in future to correlate EPR and optical data for different ion-host systems in exploring crystals for various scientific and industrial applications.

The authors are thankful to the Head, Department of Physics for providing the departmental facilities and to Prof. C. Rudowicz, Faculty of Chemistry, A. Mickiewicz. University, Poznan, Poland for CFA program.

1. Mabbs FE, Collison D, Gatteschi D (1992) Electron paramagnetic resonance of d transition metal compounds. Elsevier, Amsterdam, Netherlands.
2. Weil JA, Bolton JR (2007) Electron paramagnetic resonance: elementary theory and practical applications. (2^nd edn), Wiley, New York, USA.
3. Brik MG, Avram CN, Avram NM (2006) Calculations of spin Hamiltonian parameters and analysis of trigonal distortions in LiSr(Al,Ga)F₆:Cr³⁺ Physica B 384(1-2): 78-81.
4. Pandey S, Kripal R, Yadav AK, Açıkg¨oz M, Gnutek P, et al. (2021) Implications of direct conversions of crystal field parameters into zero-field splitting ones - Case study: Superposition model analysis for Cr³⁺ ions at orthorhombic sites in LiKSO₄. J Lumin 230: 117548.
5. Bradbury MI, Newman DJ (1967) Ratios of crystal field parameters in rare earth salts. Chem Phys Lett 1(2): 44-45.
6. Tippins HH (1965) Optical absorption and photoconductivity in the Bandedge of β-Ga₂O₃. Phys Rev 140: A316-A319.
7. Hajnal Z, Miro J, Kiss G, Reti F, Deak P, et al. (1999) Role of oxygen vacancy defect states in the n-type conduction of β-Ga₂O₃. J Appl Phys 86: 3792-3796.
8. Tomm Y, Ko JM, Yoshikawa A, Fukuda T (2002) Floating zone growth of β-Ga₂O₃: A new window material for optoelectronic device applications. Sol Energy Mater Sol Cells 66: 369-374.
9. Grank J, Fleischer M, Meixner H (1996) Electrical doping of gas-sensitive, semiconducting Ga₂O₃ thin films. Sens Actuators B 34: 373-377.
10. Orita M, Ohta H, Hirano M, Hosono H (2000) Deep-ultraviolet transparent conductive β-Ga₂O₃ thin films. Appl Phys Lett 77: 4166-4168.
11. Gesmundo F, De Asmundis C (1973) An electron paramagnetic resonance study of the solid solutions of chromia in β-Ga₂O₃. J Phys Chem Solids 34: 1757-1763.
12. Yeom TH, Kim IG, Lee SH, Choh SH, Yu YM (2003) Electron paramagnetic resonance characterization of Cr³⁺ impurities in a β-Ga₂O₃ single crystal. J Appl Phys 93: 3315-3319.
13. Geller S (1960) Crystal structure of β-Ga₂O₃. J Chem Phys 33: 676-684.
14. Ahman J, Svensson G, Albertsson J (2000) A reinvestigation of β~-gallium oxide. Acta Cryst C 52(6): 1336-1338.
15. Figgis BN, Hitchman MA (2000) Ligand field theory and its applications, Wiley, New York, USA.
16. Rudowicz C, Karbowiak M (2015) Disentangling intricate web of interrelated notions at the interface between the physical (crystal field) Hamiltonians and the effective (spin) Hamiltonians. Coord Chem Rev 287: 28-63.
17. Rudowicz C (1987) Concept of spin hamiltonian, forms of zero field splitting and electronic zeeman hamiltonians and relations between parameters used in EPR: A critical review. Magn Reson Rev 13: 1-89.
18. Rudowicz C, Misra SK (2001) Spin-Hamiltonian formalisms in Electron Magnetic Resonance (EMR) and related spectroscopies. Appl Spectrosc Rev 36(1): 11-63.
19. Rudowicz C (1985) Transformation relations for the conventional Okq and normalised O'kq Stevens operator equivalents with k=1 to 6 and –k≤q≤ J Phys C Solid State Phys 18(7): 1415-1430.
20. Rudowicz C, Chung CY (2004) The generalization of the extended Stevens operators to higher ranks and spins, and a systematic review of the tables of the tensor operators and their matrix elements. J Phys Condens Matter 16(32): 5825-5847.
21. Newman DJ, Ng B (2000) Superposition model. In: Newman DJ, Ng B (Eds.), Crystal Field Handbook, Cambridge University Press, UK, pp. 83-119.
22. Newman DJ, Ng B (1989) The superposition model of crystal fields. Rep Prog Phys 52: 699-763.
23. Rudowicz C (1987) On the derivation of the superposition-model formulae using the transformation relations for the Stevens operators. J Phys C: Solid State Phys 20(35): 6033-6037.
24. Rudowicz C, Gnutek P, Açıkgöz M (2019) Superposition model in electron magnetic resonance spectroscopy – a primer for experimentalists with illustrative applications and literature database. Appl Spectroscopy Rev 54: 673-718.
25. Açıkgöz M (2012) A study of the impurity structure for 3d³ (Cr³⁺ and Mn⁴⁺) ions doped into rutile TiO₂ Spectrochim Acta A 86(2): 417-422.
26. Müller KA, Berlinger W, Albers J (1985) Paramagnetic resonance and local position of Cr³⁺ in ferroelectric BaTiO₃. Phys Rev B 32(9): 5837-5850.
27. Müller KA, Berlinger W (1983) Superposition model for sixfold-coordinated Cr³⁺ in oxide crystals (EPR study). J Phys C: Solid State Phys 16(35): 6861-6874.
28. Yeom TH, Chang YM, Rudowicz C (1993) Cr³⁺ centres in LiNbO₃: Experimental and theoretical investigation of spin Hamiltonian parameters. Solid State Commun 87(3): 245-249.
29. Siegel E, Muller KA (1979) Structure of transition-metal-oxygen-vacancy pair centers. Phys Rev B 19(1): 109-120.
30. Rudowicz C, Bramley R (1985) On standardization of the spin Hamiltonian and the ligand field Hamiltonian for orthorhombic symmetry. J Chem Phys 83(10): 5192-5197.
31. Yeung YY, Newman DN (1986) Superposition-model analyses for the Cr³⁺ 4A2 ground state. Phys Rev B 34(4): 2258-2265.
32. Yeung YY, Rudowicz C (1992) Ligand field analysis of the 3dN ions at orthorhombic or higher symmetry sites. Comp Chem 16(3): 207-216.
33. Yeung YY, Rudowicz C (1993) Crystal field energy levels and state vectors for the 3dn ions at orthorhombic or higher symmetry sites. J Comput Phys 109(1): 150-152.
34. Chang YM, Rudowicz C, Yeung YY (1994) Crystal field analysis of the 3dN ions at low symmetry sites including the ‘imaginary’ terms. Computers in Physics 8(5): 583-588.
35. Wybourne BG (1965) Spectroscopic properties of rare earth. Wiley, New York, USA.
36. Zhang JG, Bin L, Tai XC, Jun X, Qun D, et al. (2007) Single crystal β-Ga₂O₃: Cr grown by floating zone technique and its optical properties. Sci China Ser E-Tech Sci 50(1): 51-56.
37. Adachi S (2019) Photoluminescence spectroscopy and crystal-field parameters of Cr³⁺ ion in red and deep red-emitting phosphors. ECS J Solid State Sci Tech 8(12): R164-R168.
38. Adachi S (2021) Review-photoluminescence properties of Cr³⁺-activated oxide phosphors. ECS J Solid State Sci Tech 10: 026001.