High Pressure Thermoelastic Behaviour of Intermetallic Compound MgCu at Elevated Temperatures

Intermetallic compounds in general, and Mg based alloys in particular have important applications in various fields of science and technology [1-3]. MgCu with a CsCl (B2) type structure is of current interest [4-6]. Mg-alloys are among the lightest structural materials known, exhibiting remarkable fundamental properties [7-10]. Thermoelastic properties of intermetallic compounds at high pressures and high temperatures have been investigated [11-13] using phenomenological models and ab initio calculations.

The structural and elastic properties of the intermetallic compound MgCu with CsCl-type structure have been investigated [5] using the first-principles DFT calculations [14,15]. It has been emphasized by Daoud et al. [12] that the study performed by Boucetta [5] was established only at zero pressure for the thermodynamic properties of MgCu up to a temperature of 1000K. The effect of high pressure on the thermodynamic properties of MgCu with CsCl (B2) structure has been investigated [12] using the plane-wave pseudopotential (PW-PP) method [16] within the framework of DFT.

In the present study, we use a simple analytical method based on the Grover-Saxena equation of state (EOS) [17,18]. This EOS [19] has been found to yield good agreement with the available experimental data [20-26] and ab initio results [27,28] for different types of compounds. In the present work, we use this EOS for investigating thermodynamic and thermoelastic behaviour of MgCu up to a pressure of 50GPa and temperatures up to 1000K. The model for density dependence of the Debye frequency developed by Roy [29] based on the DFT calculations [30,31] for some elemental solids, when used in the Lindemann law of melting [32,33], gives good agreement with the available experimental data [34-38]. Subsequently, Anand et al. [39] have demonstrated the adequacy of the Roy-Sarkar model also for determining melting curves of various diatomic compounds in good agreement with the available experimental data [40-42] as well as with the results based on the ab initio molecular dynamics [42-45] and the DFT-LDA method [46]. In the present study, we use the Roy-Sarkar model in the Lindemann law to determine melting curve of the intermetallic compound MgCu.

Volume of a material at high pressures and high temperatures can be determined with the help of the Grover-Saxena EOS that can be written as follows [19].

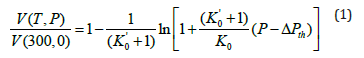
Where P is the total pressure. K₀ and K'₀ are respectively the bulk modulus and its pressure derivative, both at zero-pressure and at temperature equal to 300K. ΔP_th is the difference

Where P_th(T) and P_th(300) are the values of thermal pressure at temperatures T and 300K, respectively. It has been found by Anderson [47] that the thermal pressure changes linearly with temperature at high temperatures, and we can write [48,49]

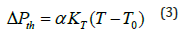
Where α is the thermal expansivity and K_T the isothermal bulk modulus, both at the initial temperature T₀= 300K. At temperatures T≥θ_D , the Debye temperature, the product αK_T remains nearly constant [47]. We have taken α = 8.35×10−5K−1 , and K_T= 59.58GPa for MgCu at ambinet conditions [12].

Expressions for bulk modulus K(T,P) and its pressure derivative K’(T,P) are obtained by differentiating Eq. (1) successively with respect to pressure. Thus, we get

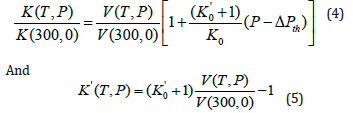
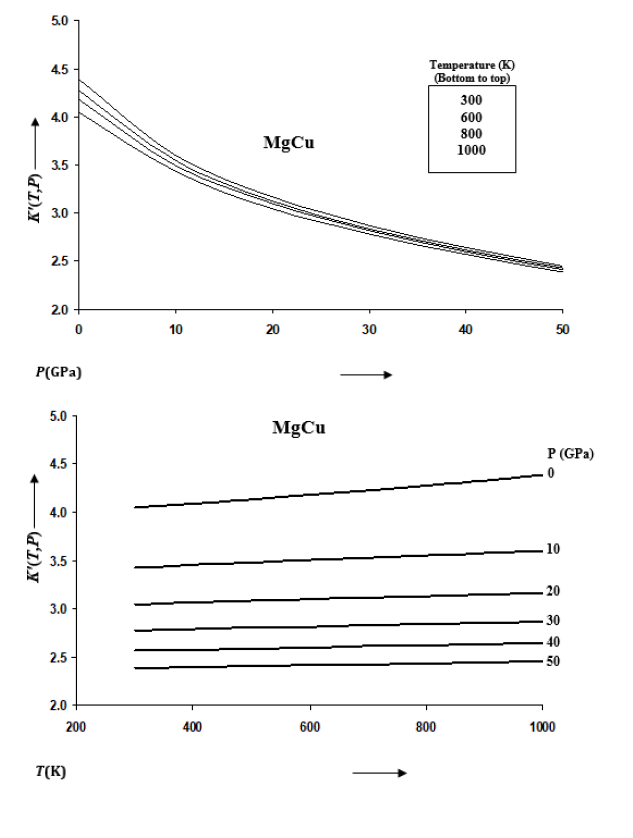
Where k₀=59.58GPa, and k'₀=4.05 for MgCu [12]. Equations (1), (4) and (5) are used to calculate V(T,P), K(T,P) and K’(T,P) for MgCu at high pressures and high temperatures. The results are given in Figures 1-3.

Figure 1:Variations of V(T,P)/ V(300, 0) with pressure along selected isotherms, and with temperature along selected isobars for MgCu shown by continuous curves (─). Symbols (●) represent the first-principles DFT calculations [12].

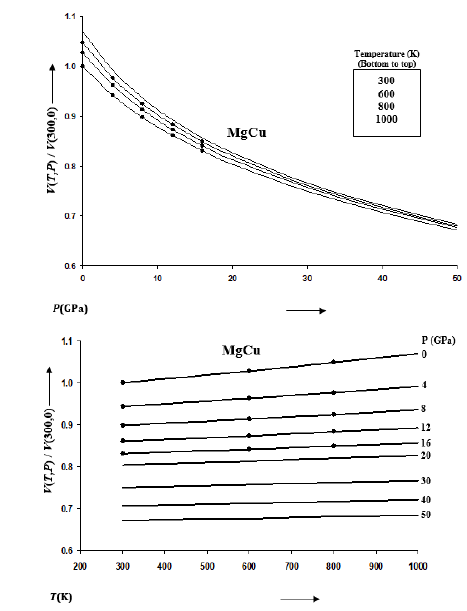
Figure 2:Variations of K(T,P) with pressure along selected isotherms, and with temperature along selected isobars for MgCu shown by continuous curves (─). Symbols (●) represent the first-principles DFT calculations [12].

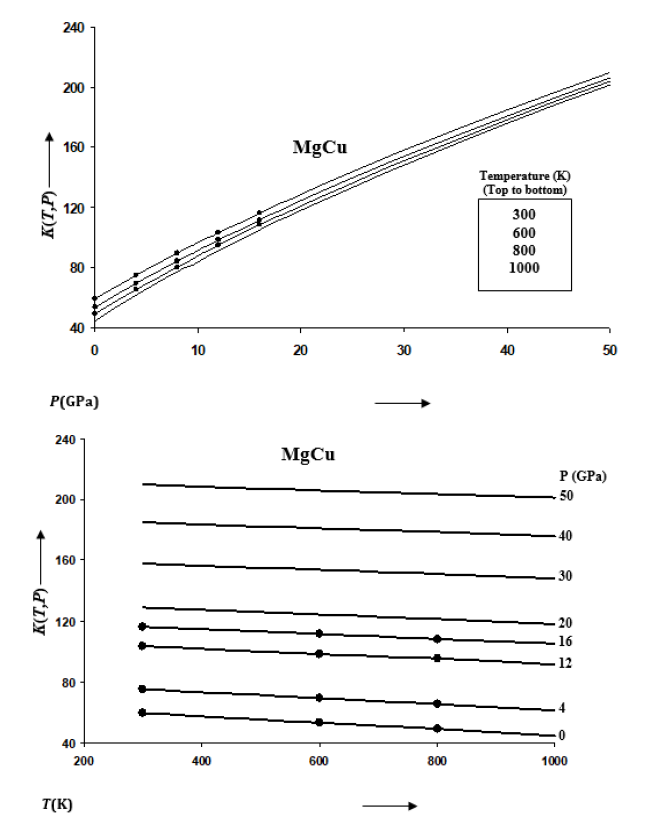
Figure 3:Variations of K’(T,P) with pressure along selected isotherms, and with temperature along selected isobars for MgCu shown by continuous curves (─).

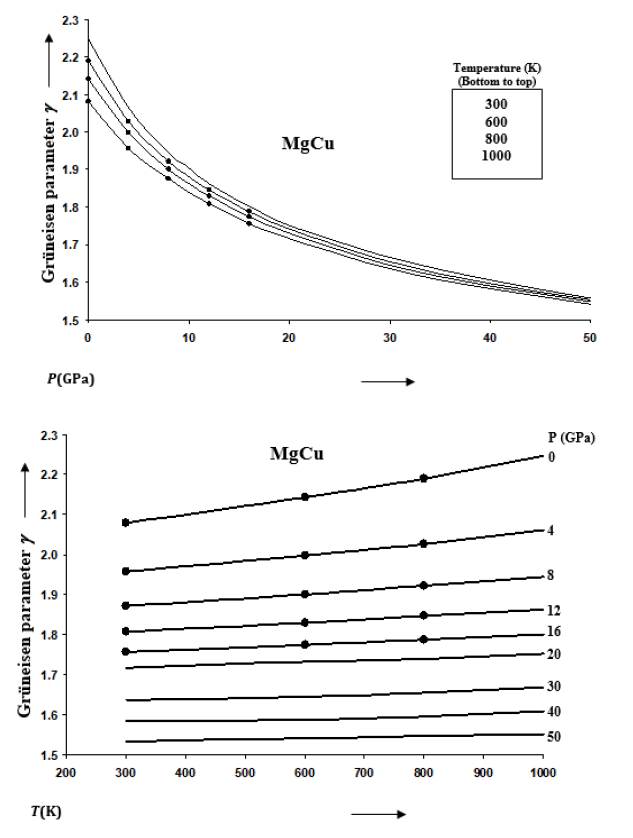
The Grüneisen parameter γ can be expressed as a function of volume ratio V/V₀ as follows [39]

Eq. (6) has been obtained [39] by using the linear dependence formulations for the Debye frequency [29]. In Eq. (6), γ₀ =γ (300,0) = 2.08 , and V₀ =V (300,0) . Values of γ for MgCu at different pressures and temperatures are shown in Figure 4. For determining the Debye temperature D θ we use the following relationship for gamma

Figure 4:Variations of Grüneisen parameter 𝛾 with pressure along selected isotherms, and with temperature along selected isobars for MgCu shown by continuous curves (─). Symbols (●) represent the first-principles DFT calculations [12].

Taking Eqs. (6) and (7) together, and then integrating we find

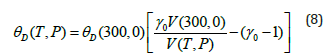
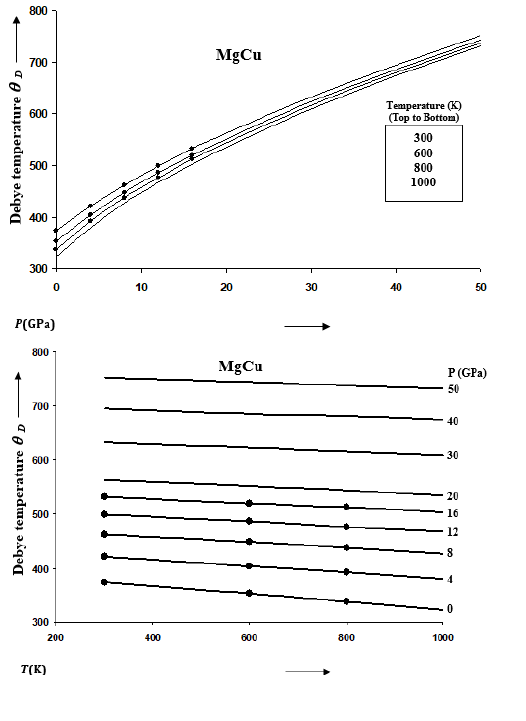
Eq. (8) has been obtained and reported for the first time in the present study. Variations of θ_D with P and T for MgCu are given in Figure 5. Value of (300,0) θ_D is equal to 373.5K for MgCu [12].

Figure 5:Variations of Debye temperature θD with pressure along selected isotherms, and with temperature along selected isobars for MgCu shown by continuous curves (─). Symbols (●) represent the first-principles DFT calculations [12].

Equation (6) for the volume dependence of gamma when used in the Lindemann law of melting [32,33] gives the following expression [29,39]

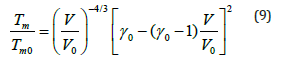
Where T_m0 is the value of melting temperature T_m at zeropressure. Values of T_m0 are available for MgCu₂ and Mg₂Cu [50] which are respectively 1093K and 990K. For the intermetallic compound MgCu, we take an intermediate value for T_m0 equal to 1042K. Melting curve for MgCu is determined from Eq. (9) by calculating melting temperatures at high pressures. An expression for the melting slope at ambient pressure (P=0) is given below [39]

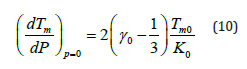
Equation (10) gives dT_m/dP at ambient pressure equal to 61KGPa-1 for MgCu. Melting slope of a material decreases with the increase in pressure because gamma decreases and bulk modulus increases with the increasing pressure [51].

Results for P-V relationship along different isotherms at selected temperatures obtained from the Grover-Saxena EOS for MgCu are shown in Figure 1. Isobaric variations of volume with temperature at selected pressures for MgCu are also shown in Figure 1. It is found that different isotherms appear to converge at high pressures.

The rate of variation of volume with temperature becomes small at high pressures. This is consistent with the thermodynamics of solids at extreme compression [52,53]. The isothermal and isobaric variations of bulk modulus K(T,P) are given in Figure 2 and those for pressure derivative of bulk modulus K’(T,P) in Figure 3 for MgCu. It is found that K increases and K’ decreases with the increase in pressure along an isotherm.

Variations of the Grüneisen parameter γ along different isotherms and isobars obtained from Eq. (6) are shown in Figure 4. It should be mentioned that Eq. (6) satisfies the thermodynamic constraints [39] for the volume derivatives of gamma in the limit of infinite pressure [54,55]. It is found that γ for MgCu decreases substantially with the increase in pressure along an isotherm, and increases slowly with the increase in temperature along an isobar. At high pressures, the variation of gamma with temperature becomes negligibly small such that γ becomes almost independent of temperature. Another physical quantity of great importance is the Debye temperature for describing the thermodynamic and thermoelastic behaviour of materials at high pressures and high temperatures. We have determined variations of θ_D with pressure as well as with temperature using Eq. (8) and the P-V-T results based on the Grover-Saxena EOS given in Figure 1. The results for the variations of θ_D ( T,P) are shown in Figure 5. The results obtained in the present study are found to compare well (Figures 1, 2, 4 & 5) with the corresponding values determined by Daoud et al. [12] using the first-principles DFT calculations for MgCu. The best fit for the data on θ_D (T, P) for MgCu [12] can be expressed as a quadratic function of temperature along an isobar

Figure 6:Variations of parameters A, B and C appearing in Eq. (11) for the Debye temperature θ_D(T,P) formulated by Daoud et al. [12].

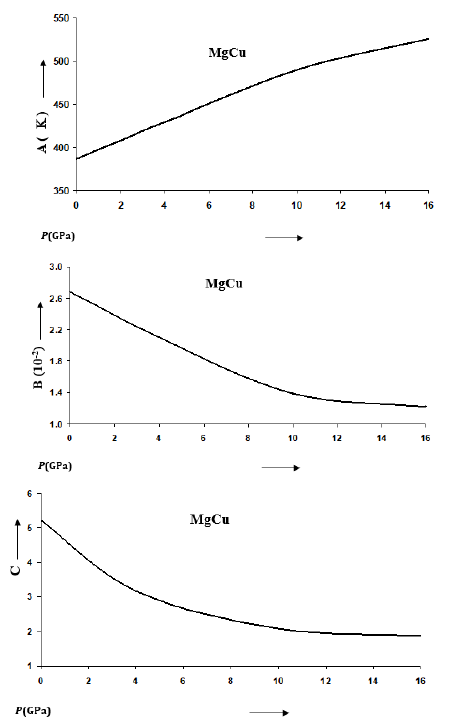
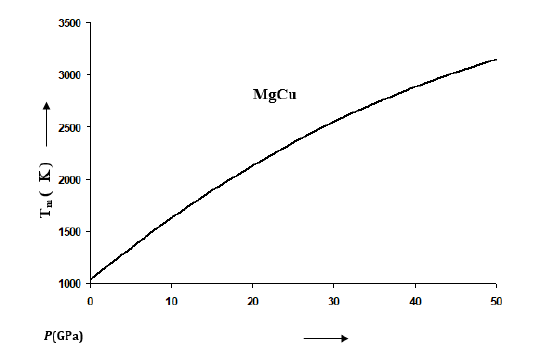
Where A, B and C are constants for a given material at constant pressure. Values of A, B and C change with the variation in pressure as shown in Figure 6 for MgCu based on the results reported by Daoud et al. [12]. Values of A increase with the increase in pressure whereas B and C decrease with P. Thus the effect of temperature is suppressed at high pressures. The rate of decreasing θ_D with temperature becomes small at high pressures. It should be mentioned that θ_D increases with the increase in pressure along an isotherm. The relationship between melting temperature and θ_D has been used in the Lindemann law [32,33] to find that Tm also increases with P. We have calculated values of Tm at different pressures for MgCu using Eq. (9), the Lindemann law based on the Roy-Sarkar model for the density dependence of Debye frequency [29]. The melting curve for MgCu thus determined is given in Figure 7. It is worth-mentioning here that the ab initio methods based on the DFT calculations and molecular dynamics simulations are very expensive and time-consuming involving heavy computations. Such attempts have also been made in case of MgCu [12] to find the results up to a pressure of 16GPa and temperatures up to 1000K. It is found that the results obtained in the present study using simple analytical methods are in extremely good agreement with the first-principles DFT calculations (Figures 1, 2, 4 & 5).

Figure 7:Melting curve of MgCu representing the variations of melting temperature Tm(K) at different pressures calculated from the Lindemann law (Eq. 9) based on the Roy-Sarkar model [29].

A simple method has been developed in the present study using the Grover-Saxena EOS for investigating the thermoelastic properties of MgCu intermetallic compound with CsCl (B2) structure up to a pressure of 50GPa. The effect of temperature up to 1000K has been taken into account in terms of thermal pressure. Pressure-volume-temperature relationships have been predicted along different isotherms at selected temperatures, and along different isobars at selected pressures. Variations of bulk modulus and its pressure derivative with the increase in pressure and temperature have also been determined.

The Roy-Sarkar model based on DFT calculations has been used to determine variations of the Grüneisen parameter and Debye temperature of MgCu with the changes in pressure and temperature. At high pressures, gamma and Debye temperature both become virtually constant, i.e. independent of temperature. The results obtained in the present study for thermoelastic properties of MgCu using simple analytical methods are very close to the first principles DFT calculations reported by Daoud et al. [12]. Using the results for volume dependence of Grüneisen parameter in the Lindemann law we have determined melting curve for MgCu up to a pressure of 50GPa. The methods used in the present study are capable of making rapid and accurate estimations of the thermoelastic properties and melting curve for MgCu.

This article is created with the support of the KEGA agency project-034STU-4/2021 “Utilization of Web-based Training and Learning Systems at the Development of New Educational Programs in the Area of Optical Wireless Technologies”.

1. Alessandro P, Scardaci D, Liampotis N, Spinoso V, Grenier B, et al. (2020) Authentication, authorization, and accounting. In: Zhao Z, Hellström M (Eds.), Towards Interoperable Research Infrastructures for Environmental and Earth Sciences, Springer, Newyork, USA.
2. Das A, Bonneau J, Caesar M, Borisov N, Wang XF (2014) The tangled web of password reuse. In: Jonsson J, Kalisky B (Eds.), Public-Key Cryptography Standards (PKCS), Internet Engineering Task Force, Fremont, California, USA.
3. (2020) New research: Most people have 70-80 passwords. Newswire, London, UK.
4. Desmond B, Richards J, Allen R, Lowe-Norris AG (2013) Active directory. (5^th edn), O'Reilly Media, Sebastopol, California, USA.
5. Microsoft (1993) Microsoft workgroup add-on for windows, user's guide, Microsoft Corporation, Bothell, Washington, USA.
6. Hunter LE (2005) Active directory field guide. (1^st edn), Apress, New York, USA, pp. 352.
7. Neuman C, Yu T, Hartman S, Raeburn K (2005) The kerberos network authentication service (V5). Network Working Group, Internet Engineering Task Force, Fremont, California, USA, pp. 1-138.
8. Karel B (2019) Cryptography is all around us, CZ.NIC, Prague, Czech Republic, Europe.
9. Conrad E, Misenar S, Feldman J (2015) CISSP studz guide. (3^rd edn), Elsevier, Amsterdam, Netherlands.
10. https://learn.microsoft.com/en-us/previous-versions/windows/it-pro/windows-server-2012-R2-and-2012/dn408190(v=ws.11)
11. Grillenmeier G (2021) Now's the time to rethink Active Directory security. Network Security 2021(7): 13-16.
12. Brabety S (2020) Penetration testing mit mimikatz. (edn), O'Reilly Media, Sebastopol, California, USA.