Pressure Effect on Humidity Diffusion through Polyester/Glass Fiber Composite in Sea Water

Composite material has been more and more utilized in the industrial fields, due to the advantages that offers like high resistance and light weight. However, when it is utilized, composite material is exposed to extreme environmental conditions like temperature and humidity, which have negative effects on the material proprieties. It causes a decrease of the material proprieties and its life durations, which can be fatal in the safety side. Therefore, the utility of studying the hygrothrermal behavior of a composite material.

Humidity absorption is explained by two theories: the molecular approach linked to the hydrophilic character of the material. The hydrophilic sites linked to the diffusing molecules through hydrogen bonds [1]. Also, it is explained by the free volume theory, related to the number and size of the free volumes existing in the material. It determines the amount of absorbed humidity [1,2]. The humidity diffusion through composite material causes a swelling and a plasticization of the matrix [2]. Moreover, it induces a decrease of the fibers resistances, a debonding of the matrix/fiber interface [3,4] and a decrease of the transition temperature (Tg) [3,5].

The humidity diffusion is influenced by different parameters like the temperature; [6,7] proved that the augmentation of the temperature induces an increase of the diffusion coefficient and the amount of absorbed humidity, as it provides more agitation to the diffusing molecules [8]. Likewise, the pressure effect in the hygrothermal behavior of a composite material is investigated: [9] demonstrated that the rise of the hydrostatic pressure accelerates the diffusion phenomena, as a result the diffusion parameters increases. These results are confirmed in the case of a polyester/glass fiber composite [10,11] showed that the elevation of the pressure generates an augmentation of the diffusion coefficient and the amount of absorbed humidity.

Furthermore, the humidity absorption kinetics is analyzed: [12] showed that humidity diffusion through the polyester/glass fiber composite follows the Fick’s Law. Likewise, [13] proved that that humidity diffusion through a glass fiber-reinforced plastic composite presents a Fickian behavior at low temperature. Also, [4,13] affirmed that humidity absorption follows the Fick’s law.

Theoretical aspects on absorption in composite material

The humidity diffusion parameters are the diffusion coefficient (D) and the amount of absorbed humidity (M_m). These parameters are influenced by the temperature [14,15]. The diffusion coefficient is calculated using the following formula [16]:

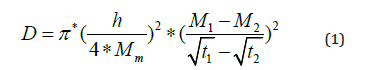
Where h: the thickness, M_m: the amount of absorbed humidity at saturation and M₁,M₂ are the amount of absorbed humidity at t₁,t₂ respectively.

The humidity diffusion process is described the one dimensional Fick’s second law [17]: 

Where t is the time, D is the diffusion coefficient, C is the concentration of the diffusing and x is the distance through the sample thickness. The diffusion absorption should respect the boundary conditions expressed in equation (3):

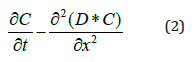
Where C_i: the initial concentration, h: the sample thickness and C_m: the concentration at the saturation. Jost [18] presents the solution of equation (2) :

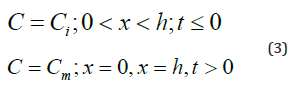
Where C_i: the initial concentration, h: the sample thickness and C_m: the concentration at the saturation. The concentration gradient from each side of the material surface generates a proportional flow. The flow can be expressed by equation (5) [19]:

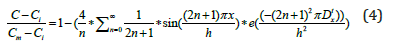
Where D: the diffusion coefficient, C: the concentration, Ɵ: the temperature, s: the solubility, P: the pressure, K_p: the pressure stress factor and K_s: the soret effect.

Material

The polyester/glass fiber composite is composed of an unsaturated polyester resin reinforced by unidirectional E-glass fiber. The glass fibers are provided by the Owens Corning Fiberglass Company and the polyester is supplied by the Reichold Chemicals Inc Company. Fillers additives, Aluminum Silicate Pigments (ASP400), are inserted to the composite material. It is a clay powder with an average size of 4.8 µm. It is added in order to increase the productivity and decrease the formation of rich resin zones [20]. The composite material is manufactured by the pultrusion technique. It is a continuous composite material manufacturing process [21]. The samples present a dimension of 20*8*6.3mm. (Table 1) exposes the volume percentage of the components of the polyester/glass fiber composite. The composition of two varieties (A and B) is presented in (Table 1).

Table 1: Composition of two variants (A, B) of the polyester/ glass fiber material [12].

Experimental methods

Water absorption test: The experimental device is presented in (Figure 1), the sample is fixed in the experimental assembly, and the container is filled with sea water, heated to the desired temperature thanks to a heating resistance. The humidity diffuses through one lateral side of the sample, the exposed pressure is fixed by the handle and is displayed on the manometer. Periodically, the sample is removed from the experimental device, dried with an absorbent paper and weighted with a Gibertini E-42-B electronic scale with an accuracy of 0.1mg. After that, the sample is put back in the experimental device. The humidity diffusion process is examined under 2,3,5,9,20,30,40 and 50

Figure 1: Designed device for absorption process.

Equation (7) presents the humidity content:

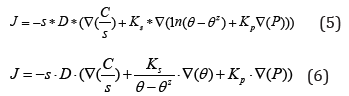
Where Mt is the material weight at instant t and M0 is the initial material weight.

Simulation of the water absorption: The Fick’s law described the humidity absorption process [19]:

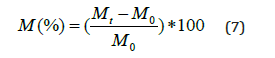
Where D is the diffusion coefficient, x is the direction of diffusion and C is the humidity concentration in the material. The diffusion coefficient (D) is expressed at each temperature through the Arrhenius law [22]:

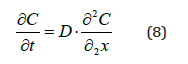
where D0 is the Arrhenius constant, T is the temperature, R is the perfect gas constant and E is the activation energy. In order to simulate the hygrothermal behavior of the polyester glass fiber composite, the finite element method is employed. The humidity diffusion in made through one lateral side and the initial humidity concentration inside the material is equal to zero. A DC3D8, a three-dimensional solid contained in the heat transfer/mass diffusion element library [23], is used. The UTEMP subroutine ensured the thermo-diffusion coupling. The results are normalized as regards to the thickness.

In this section, we present a comparison of the experimental and numerical results of the humidity diffusion through the polyester/ glass fiber composite. (Figures 2-7) present a comparison between experimental and numerical results of the humidity diffusion through the material (A) and material (B), respectively.

Figure 2: Humidity absorption curve over the time, normalized to the thickness of the materialsample (A)at 25°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

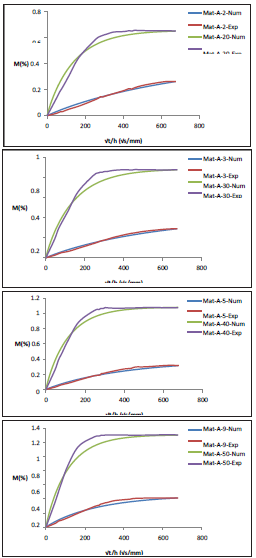
Figure 3: Humidity absorption curve over the time, normalized to the thickness of the materialsample (A)at 45°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

Figure 4: Humidity absorption curve over the time, normalized to the thickness of the materialsample (A)at 65°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

Figure 5: Humidity absorption curve over the time, normalized to the thickness of the materialsample(B)at 25°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

Figure 6: Humidity absorption curve over the time, normalized to the thickness of the materialsample(B)at 45°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

Figure 7: Humidity absorption curve over the time, normalized to the thickness of the materialsample(B)at 65°C: a. 2/20 bar, b. 3/30 bar, c. 5/40 bar, d. 9/50bar.

The humidity absorption presents a two-parts behavior: a first linear part, during which an equilibration of the concentration gradient takes place on each side of the material surface. The second part is concave to the axis of the abscissas. It is a phase of physical and chemical equilibrium inside the material. At a temperature equal or superior to 65 °C, we note a fall of the absorption curve. In fact, when osmotic pressure exceeds a critical value, the stress concentration at a point of the free volume induces the propagation of cracks inside the material. When the cracks coalesce, certain molecular chains get loose. Therefore, the absorption curve falls [24].

The rise in the pressure improves the diffusion coefficient and the amount of absorbed humidity [25]. The pressure elevates the humidity flow diffusing inside the material. Consequently, the humidity diffuses rapidly [26]. Also, the augmentation of the temperature induces an increase of the diffusion parameters, as the temperature offers more agitation to the diffusing molecules [27].

Material (B), having a higher percentage of fillers additives, absorbs a higher amount of humidity than material (A). In fact, the fillers additives reduce the rigidity of the interface matrix/fiber, facilitating the absorption process.

This research presents an analysis of the humidity diffusion through polyester/glass fiber composite. The pressure effect on the hygrothermal behavior of the composite material was examined. At high temperature, the humidity absorption presents a fall; it is due to the coalescence of cracks, caused by the stress concentration at the free volume. As a result, some molecular chains get loose. The augmentation of the pressure increases the diffusion coefficient and the amount of absorbed humidity. Also, the rise of the temperature and the percentage of fillers additives induce a rise of the diffusion parameters.

The finite element method was used to numerically reproduce the experimental results of the diffusion process. The comparison between experimental and numerical results showed that the humidity diffusion behavior through the polyester glass fiber composite can be predicted. As a perspective, we are investigating the pressure direction on humidity absorption.

1. Bonniau P, Bunsell A (1981) A comparative study of water absorption theories applied to glass epoxy composites. Journal of Composite Materials 15(3): 272-293.
2. Huang G, Sun H (2007) Effect of water absorption on the mechanical properties of glass/polyester composites. Materials & Design 28(5): 1647-1650.
3. Barjasteh E, Nutt SR (2012) Moisture absorption of unidirectional hybrid composites. Composites Part A: Applied Science and Manufacturing 43(1): 158-164.
4. Shiva Eslami F, Fathollah T (2012) Effects of aging temperature on moisture absorption of perforated GFRP. Advances in Materials Science and Engineering 2012: 4-7.
5. Wu L, Murphy K, Karbhari VM, Zhang JS (2002) Short-term effects of sea water on E-glass/vinylester composites. Journal of Applied Polymer Science 84(14): 2760-2767.
6. Ounaies M, Harchay M, Dammak F, Ben Daly H (2018) Prediction of hygrothermal behavior of polyester/glass fiber composite in dissymmetric absorption. Journal of Composite Material 52(29): 4001-4007.
7. Ben Daly R, Ben Brahim H, Hfaied N, Harchay M (2007) Investigation of water absorption in pultruded composites containing fillers and low profile additives. Polymer Composites 28(3): 355-364.
8. Onishi SE (2015) Effect of particle loading, temperature and surface treatment on moisture absorption of CFB fly ash reinforced thermoset composite. International Journal of Chemical Engineering and Applications 6(1): 6-11.
9. Pollard AP, Baggott R, Wostenholm GH, Yates B, George A (1989) Influence of hydrostatic pressure on the moisture absorption of glass fibre-reinforced polyester. Journal of Materials Science 24: 1665-1669.
10. Harchay M, Bendaly H (2009) Effet de la nature et des caractéristiques du milieu d’immersion sur le comportement hygrothermique des composites polyester/fibre de verre. 19ème Congrès Français de Mécanique 24-28: 1-6.
11. Hamidi YK, Aktas L, Altan MC (2011) Effect of repeated loading on moisture absorption of fiber reinforced polymer composites. 27^th World Congress of the Polymer Processing Society, pp. 1-10.
12. Ben Daly H, Harchay M, Belhadjsalah H, Boukhili R (2009) Experimental characterization and numerical simulation of the humidity absorption process in glass reinforced composites under dissymmetric exposure conditions. Polymer Composites 30(12): 1825-1836.
13. Eslami S, Honarbakhsh A, Eslami S (2015) Effects of moisture absorption on degradation of E-glass fiber reinforced Vinyl Ester composite pipes and modelling of transient moisture diffusion using finite element analysis. Corrosion Science 90: 168-175.
14. Harper J, Naeem M (1989) The moisture absorption of glass fibre reinforced vinylester and polyester composites. Materials & Design 10(6): 297-300.
15. Loos AC, Springer GS, Sanders BA, Tung RW (1980) Moisture absorption of polyester-E glass composites. Journal of Composite Materials 14(2): 142-154.
16. Ellyin F, Maser R (2004) Environmental effects on the mechanical properties of glass-fiber epoxy composite tubular specimens. Composites Science and Technology 64(12): 1863-1874.
17. Mbou ET, Njeugna E, Kemajou A, Sikame N, Ndapeu D (2017) Modelling of the water absorption kinetics and determination of the water diffusion coefficient in the pith of raffia vinifera of bandjoun, cameroon. Adv Mater Sci Eng 2017: 1-12.
18. Jost W (1960) Diffusion in solids, liquids, gases. Angewandte Chemie 65(19): 496.
19. Simulia D (2014) ABAQUS/CAE User ’s Manual. Simulia, USA, Pp. 1-81.
20. Kaolin functional fillers for pultrusion put BASF performance minerals extenders to work. BASF The chemical company, Germany.
21. Pultrusion,
22. Kang H, Hart CA (1997) Temperature effect on diffusion coefficient in drying wood. Wood and Fiber Science 29: 325-332.
23. (2014) Massachusetts Institute of Technology, “CD3D8”.
24. Ashbee KG, Frank FC (1967) Water damage in polyester resins. 300(1463): 196.
25. Bunsell AR, Avena A (1988) Effect of hydrostatic pressure on the water absorption of glass fibre- reinforced epoxy resin. Composites 19(5): 355-357.
26. Jean-Pierre P, Sauterau H, Verdu J (2002) Thermosetting polymers.
27. Bouchama B, Chateauneufe A, Adda B (2008) An uncertainty method for moisture concentration assessment in composite material plates t300/5208 under hygrothermal conditions effects. J Eng Environ Sci 32: 253-263.