The Rotating Magnetic Field for Confining and Heating Plasma

To retain and simultaneously heat the high-temperature plasma, it is proposed to use a magnetic trap creating a closed rotating magnetic field. Such a magnetic field is created by applying magnetic fields from nine open traps placed in triads in three orthogonal planes. Each trap is connected to one of phases of a three-phase AC circuit and is set at 120 degrees to the other two traps located in this plane.

If we consider that the only way to effectively confine plasma in a certain volume is the magnetic field of a trap of a particular configuration, it is proposed to create a reactor based on a combination of nine magnetic traps. These traps block plasma escape in all three directions, and at the same time allow it to heat up to the fusion temperature of several tens of keV due the rotating magnetic fields in three orthogonal planes.

The magnetic field of the proposed reactor is created by a combination of spatially overlapping magnetic fields of the simple open traps. The traps are placed in triads in three orthogonal planes. Each of them is connected to one phase of the three-phase AC power grid with industrial frequency. Coplanar traps are placed on a circle with a common center, each at 120 degrees to the other two.

Coils of these nine traps lie in a sort of spherical surface and due to overlapping of the magnetic fields create in its center the total magnetic field with a constant magnetic induction vector, which rotates with the frequency of the three-phase current supplied to the coil.

Three open traps in the same plane create a magnetic field rotating in this plane with the frequency of the three-phase current supplied to the coils, and a constant vector of the magnetic induction B. Each coil creates its own magnetic field

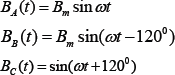
The total magnetic induction vector in the center is 1.5 B_m, and rotates with angular frequency ω

Let's see how the solenoids of the traps placed in three orthogonal planes are to be phased, in order to obtain a closed magnetic field, the total magnetic induction vector of which rotates continuously in all three dimensions.

In the X-Y plane, projections of the total vector of the magnetic induction on the X and Y axes will be:

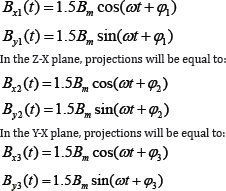
where φ1, φ2, φ3 are initial phases of total vectors of magnetic induction in the planes in question.

In the Z-X plane, change of α(t) along the Z-axis (in the direction of the X axis) is equal to:

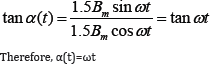
In the X-Y plane, change of β(t) along the X-axis (in the direction of the Y-axis) is equal to:

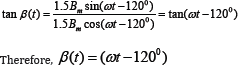
In the Y-Z plane, change of γ(t) related to the Y-axis (in direction of the Z-axis) is equal to:

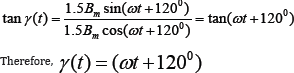
Hence we can make the following conclusion: all projections of the resultant magnetic induction vector B(t) rotate with the same angular velocity, each in its plane, and each is offset in time by one third of the period with respect to each other, where each projection B(t) is formed by superposition of the magnetic fields of the three open traps located in the same plane and offset in space of this plane by one third of the circle. These traps induce sinusoidal magnetic fields in time, which are also offset in time relative to each other by one third of the period.

The resulting configuration of the magnetic field allows asserting that the area in the center of the reactor will look like a cage, spokes of which will be lines of the magnetic field obtained by over-imposing three equal magnetic fields rotating in three orthogonal planes. Such a closed configuration does not guarantee the possibility of obtaining required concentration and temperature of heated plasma.

To solve this problem, authors propose to initially place a capsule in the form of a layered capsule in the form of calibrated ball of deuterium-tritium (D-T) mixture with the density of ⟦10 ⟧^19 ⟦cm⟧^(-3) in the center of the reactor. The ball should be made as a set of coaxial spherical D-T layers separated by thin metal shells made of sheets of lithium 6. When plasma with the energy of ⟦10⟧^2-⟦10⟧^3keV is injected, the target will heat up, and concentration of plasma will gradually rise simultaneously in the whole volume due to the vortex currents induced by external rotating magnetic fields of closed configuration. This design of the source of D-T mixture will make it possible to, if not eliminate, then to significantly reduce uneven heating of the plasma on the surface layer of the container.

In a first approximation, using a system of traps that create a rotating magnetic field can ensure plasma confinement. To do so, in the center of the spherical volume of the reactor a container with a D-T mixture with specified density should be placed. The target should be heated by the high temperature plasma injected into the working volume from an external source. After getting into the working volume and warming up due to vortex currents induced by external magnetic fields, it will heat up in the center of the container with the D-T mixture. As the container heats up and is destroyed, the mixture will ionize, heat up and will be kept in the central area of the working volume due to collisions of neutral atoms of deuterium and tritium with ions of initially injected plasma and ionized ions of the target.

A possibility appears for simultaneous plasma heating and confinement in a given volume,

The need to use superconductivity in order to achieve magnetic field intensity up to 7T is excluded,

Possible escape of the plasma from the specified volume when the current velocity vector becomes parallel to the induction vector of the resulting rotating magnetic field in a short time, can, with sufficient density of the equilibrium plasma, be compensated for by electrostatic processes inside the plasma, the D-T mixture should be heated with both ionization and confinement.

This work was supported by MEPhI Academic Excellence Project (contract No. 02.a03.21.0005, 27.08.2013).