Experimental and Theoretical Studies of Heat Transfer in Graphene/Agar under Laser Irradiation

The extraordinary development of nanomaterial provides tremendous opportunities in biomedical filed, including disease therapy [1,2], biodetection [3], bioimaging [4] and biodevices [5]. In bioapplications, temperature is a critical parameter especially in hyperthermia therapy, drug delivery and clinical surgery. In hyperthermia therapy, elevated temperature would cause apoptosis and necrosis of abnormal cells. It has been reported that protein unfolding and aggregation occurs above 41 °C, causing irreversible damages with long time (>60min) irradiation. Above 48 °C, DNA are damaged and irreversible damages occur with only 4min-6min irradiation [6]. Therefore, numerous studies focused on raising temperature in abnormal tissues such as tumors to achieve therapeutic effects have been widely performed. In addition, elevating temperature in thermo-responsive drug carriers effectively triggers drug release. Controlled doxorubicin (DOX) release was achieved by a graphene oxide-silver nanoparticles (GO@Ag) nanocomposite drug carrier through manipulating laser irradiation to change temperature of the nanocomposite [7]. Besides hyperthermia therapy and drug delivery, elevating temperature by various techniques such as laser welding and microwave heating has applied in surgical resection for years, which has gained excellent therapeutic capability [8,9].

To raise temperature in biological tissue or drug carriers, susceptors which can absorb electromagnetic energy like microwave and radiofrequency and convert it to thermo-energy are essential. It was demonstrated that graphene nanosheets is an exceptional suceptor of radio frequency energy, microwave and laser according to its low density, low cost, large surface to volume ratio, controllable shape/size and tunable functionalization. Also, organic molecules conjugated graphene with enhanced NIR light absorption has outstanding photothermal therapy effects [2]. Moreover, because of its high absorbance of radio frequency energy and microwave energy, graphene is an effective radio frequency induced and microwave induced hyperthermia agent [10-12].

In comparison to radio frequency and microwave, laser light has controllable size and dimensions which is more suitable for targeting irradiation. Laser heating or laser welding used for clinical surgery and disease therapy has been proposed for years. In laser heating, uniform temperature distribution in the designated area is desired to maximize therapeutic effects and surgery efficiency. Infrared (IR) camera was commonly used to monitor surface tissue temperature in photothermal process. However, it cannot reveal the temperature profile under the skin, in which temperature might be much higher than the surfaces. Therefore, computer simulation is another robust method to investigate the temperature profile inside the tissues. Temperature evolution in tissues with large blood vessels has been studied by finite element modelling, demonstrating that the shape of surface isotherms were related to the orientation and blood flow rate inside the tissue [13]. And laser welding of cornea was also studied under different laser powder densities by finite element modelling [14]. Though lots of efforts have been done on the finite element modelling of the laser heating in metal manufacturing field and in bare biological tissues, no studies focused on temperature evolution of tissues with nanoparticles injections [15,16].

Therefore, in this paper, experimental studies and finite element modelling were carried out to investigate temperature evolution of graphene derivatives hydrogels. Due to the fact that the similarity of light absorption property and porous characteristic between agar gels and tissue, graphene oxide was embedded in agar gels to mimic the heating paths in biological tissues [15]. Assisting with IR camera, temperature profile of surfaces of GO/agar and bare agar hydrogels were captured, revealing the enhanced thermal conversion with GO. Moreover, a two-dimensional finite element method model was presented in this paper to quantify the heating effects on GO with various particles distribution, absorption ability, thermal conductivity under laser irradiations with different power, providing some clues for controlling the temperature raising for biomedical applications.

Materials

Graphite was purchased from Asbury Carbons, and nitric acid (HNO₃), sodium chlorate (NaClO₃) were from Sigma-Aldrich.

Synthesis of GO/agar

GO was prepared by the modified Brodie's method [17]. Specifically, 500mg of graphite were oxidized by a mixture of 80ml of HNO₃ and 4.25g of NaClO₃. The mixture was stirred at room temperature for 24 hours. The sample was diluted with water and then neutralized with sodium hydroxide. After that, the sample was washed and collected by centrifugation to obtain graphite oxide. Graphite oxide was mixed with ammonia hydroxide, and exfoliated into GO by ultrasonication for 2 hours. The exfoliated GO was collected by centrifugation at 5000rpm for 30 minutes to remove the large sediment.

Agar hydrogel was used to simulate tissue to measure the photo-to-thermal conversion phenomenon. Specifically, GO was dispersed in deionized (DI) water with concentration of 100μg/ ml, subsequently, 20mg/ml agar was added in the sample. The mixture was heated to 95 °C in an oil bath with continuous stirring to dissolve the agar. After that, the mixture was injected to a mold with a dimension of 15mm*15mm*5mm and cooled down at 4 °C for 2 hours. Then the gel was released from the mold to perform the measurement.

Temperature measurement of GO/agar

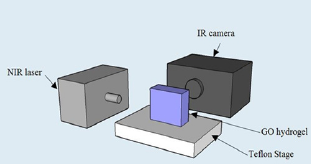
Temperature change of the gels under continuous 808-nm laser irradiation (2.5W/cm²) was monitored by a FLIR SC8303 highspeed infrared camera. The camera was placed directly in front of the agar gel, recording two-dimensional transient temperature distribution images (Figure 1). The viewing area of the samples and holder was set at a 640*360-pixel window frame size, with an acquisition rate of 2 frames per second.

Figure 1: Schematic experimental set-up for temperature measurement of GO/agar under NIR laser irradiation.

Governing equations

Numerical simulation was performed with COMSOL Multiphysics 4.4. Because of the porous characteristic of agar gel, a 2D model coupling porous flow and convection-conduction equations was built. The flow in porous agar gel was described by Brinkman equation, which is an extension of Darcy's law by including a term for momentum transport within the porous media due to shear stress. The resulted velocities in Brinkman equation was then linked to the heat transfer in porous media interface, while the heat transfer in solids modulus was applied into graphene derivatives domain.

In the porous media, fluid can move within the porous matrix but not exit from it, where is described by Brinkman equation with time dependent characteristic as following [18]:

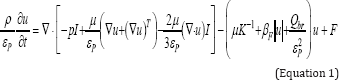
Where T is temperature, t is time, ρ is density, u is the velocity vector, ε is the porosity, μ is the permeability of the porous medium, μ is dynamic viscosity, β is the Forchheimer term and Q_br is a mass source or mass sink.

The heat transfer in solids equation described the temperature profile in graphene derivatives [19]:

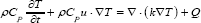
Where T is temperature, t is time, ρ is density, C_P is heat capacity, u is thermal conductivity, Q is the velocity vector and Q is the heat source term. It is assumed that agar gel is transparent to NIR laser, so Q is supposed to be null everywhere except in the graphene derivative domain in y∈(2.5mm,12.5mm) [14], being:

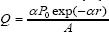
Where α is the absorption coefficient of graphene derivatives, P₀ is the continuous wave diode laser power output, A is the spot area 0.6cm² with 1cmx 0.6cm, and r is the propagation length of the laser light. Unless specified otherwise absorption coefficient α of GO domain was 10cm^-1 [20], and laser power was 1.5W in the models.

In the porous media (agar gel), a time-dependent equation was selected [21]:

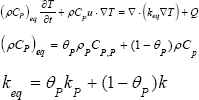
Where θ_p stands for volume fraction of the matrix P, K_eq is the thermal conductivity of matrix and fluid material and porous matrix. In Equation 4, u is the velocity vector obtained by the Brinkman equation.

Boundary conditions

The initial temperature of the model was consider as T₀=20 °C, while the convection coefficient of the gel-air boundary was h=20 W/(m•K)[14].

Numerical simulation

Figure 2: Illustration of 2D thermal model of agar gel containing GO inclusions with surface ratio of 4%.

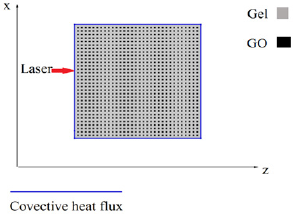
The geometrical depiction of a general 2D model was illustrated as Figure 2. However, in the 2D model, instead of using individual graphene nanosheet with size in nanometres, a series of square inclusions in the size of millimetres were used to stand for the graphene nanosheet to save the computation expense (Figure 3).The value of absorption coefficient, heat capacity and other physical parameters are listed in Table 1. A COMSOL Multiphysics (COMSOL Multiphysics 4.4, Burlington, MA) software based on finite element method were used to solve the couple heat transfer in porous media and heat transfer in solids with temperature tolerance of 0.0001. A tetrahedral meshing scheme was used to calculate the model.

Figure 3: Geometry of 2D models of GO inclusions (a)1x1, (b) 4x4, (c)8x8, (d)16x16,(e) 32x32,(f) 4x(8x8). The area of GO inclusions in each model was 0.09 cm², which accounts 4% of total area.

Table 1: Physical Constants used in simulation.

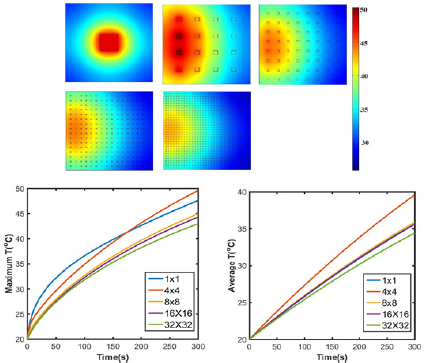
Since the computation expense for nano-sized graphene by COMSOL was too high, grapheme inclusions were used to stand for graphene nanosheets. As shown in Figure 4, except for 4x4 inclusions, maximum temperature generally decreases with increasing number of inclusions under same irradiation conditions because of the smaller size of the heat source domain graphene. The maximum/average temperature in 16x16 and 32x32 are 44.3 °C/35.6 °C and 43.0 °C/34.4 °C, in which the differences are 2.93% and 3.37% respectively. Therefore, 2D models with 16x16 and 32x32 inclusions are considered accurate enough to represent nano-sized graphene in the simulation.

Figure 4: (a) Simulated temperature profile of GO inclusions 1x1, 4x4, 8x8, 16x16, 32x32 embedded agar gel after 5 minutes’ NIR laser irradiation; (b) Maximum and (c) average temperature of GO/agar.

Comparison of experimental and simulation results

During the experiment, surface temperature profile of agar hydrogel and GO/agar was captured by IR camera. The experimental results show that without embedding with GO, temperature barely increases after laser irradiation because of the low NIR light absorption. However, after embedding with GO, maximum temperature on the surface of hydrogel can reach to above 45 °C, indicating that the enhanced photo to thermal conversion of hydrogel by GO. Meanwhile, the geometry of temperature profile in GO/agar is not symmetric due to that the hydrogel was placed on a Teflon stage during the measurement. Different with experiment, the shape of temperature profile in simulated GO/agar is symmetric semicircle because this 2D model studies the temperature change inside of the gel instead of surface temperature on the front faces as in experiment. Therefore, Figure 5 indicates that inside of the hydrogel, temperature profile shows different shape with the surfaces of the hydrogel because of only four boundaries has convective heat flux inside hydrogel, but on the surfaces, the entire surfaces has convection with surrounding air.

Figure 5:
5a: Temperature profile of agar hydrogel after 5 minutes’ NIR laser irradiation;
5b: Experimental and
5c: Simulated temperature profile of GO/agar after 5 minutes’ NIR laser irradiation.

Parametric study

Parametric study was also used to extract the important factors which affected the temperature profile of agar gel, providing some guidelines for photothermal or laser welding material and experimental design. Absorption coefficient, thermal conductivity, laser power and nanomaterial aggregation were investigated in this study. The absorption coefficient of graphene derivatives is easy to be modified through conjugation or exfoliation, while thermal conductivity of graphene derivatives ranges from ~20W/(mK) to ~5000 W/(mK) according to its lateral size, oxidation and layers [30,31].

Effects of absorption coefficient: Due to the relatively low NIR light absorption of GO compared to other metal nanoparticles, photosensitizer were used to enhance its light absorption by covalent or noncovalent conjugation [32,33]. Herein, heating behavior of GO under laser irradiation with different absorption coefficient was compared. As shown in Figure 6, temperature distributions were similar with different absorption ability, exhibiting a semicircle shape approximately. Maximum temperature reaches to 49.3 °C when absorption coefficient is 20cm^_1, 14.7% higher than the one of absorption coefficient 10cm^_1. Specifically, maximum and average temperature in agar gel are higher with higher absorption coefficient, meanwhile, temperature gradient is also larger with higher absorption coefficient since laser light intensity attenuates faster when absorption is higher.

Figure 6: Temperature profile of GO/agar with absorption coefficient (a) a=10cm^-1, (b) a=15cm^-1 and (c) a=20cm^-1. (d) Maximum and (e) average temperature of GO/agar; (f) Temperature distribution along z axis at x=7.5mm.

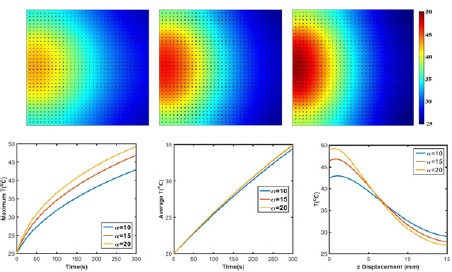
Figure 7: Temperature profile of GO/agar with graphene thermal conductivity (a) k=80W/(mIv), (b) k=500W/(mIv), (c) k=1000W/ (mK). (d) Maximum and (e) average temperature of GO/agar. (f) Temperature distribution along z axis with x=7.5mm.

Effects of thermal conductivity: Thermal conductivity is another critical physical property which affects heat transfer behavior of graphene, as shown in Equation 2. Figure 7 show that higher thermal conductivity lowers the temperature slightly because of the faster heat dissipation in GO/agar. With 12.5 times increase in thermal conductivity (k=1000W/(mK) vs. k=80W/ (mK)), temperature distribution over the 2D surface and along x axis is only 0.02% higher than k=80W/(mK). Considering the light absorbed graphene nanosheets is with only nano-size dimension, VT in Equation 2 is possible to approach to zero so that thermal conductivity barely affect the temperature profile.

Effects of laser power: The temperature alterations caused by laser power were investigated with absorption coefficient 10cm^{- 1}. Compared to absorption coefficient, increased laser power has more significant impacts on temperature rising. An increase of ~15% occurs with increasing absorption coefficient from 10cm^{- 1} to 20cm^-1. On the other hand, maximum/average temperature increases 43.0 °C/34.4 °C to 65.9 °C/48.8 °C, resulting in about 40-50% of temperature rising when p=3W compared to p=1.5. Moreover, unlike the effects of absorption coefficient, it shows higher temperature along the z axis from 0mm to 15mm at x=7.5mm with higher laser power irradiation. This is due to the fact that more light falling on the surface of the gel with increasing laser power, and the attenuation of laser is independent of laser power inputs because of the unchanged absorption coefficient of the material (Figure 8).

Figure 8: Temperature profile of GO/agar with laser power (a) p=1.5W, (b) p=2W and (c) p=3W. (d) Maximum and (e) average temperature of GO/agar. (f) Temperature distribution along z axis with x=7.5mm.

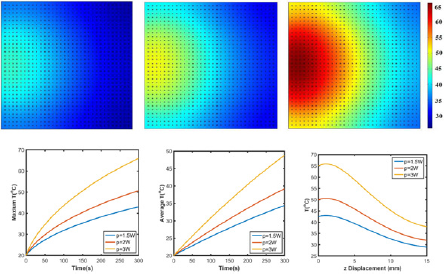
Figure 9: Temperature profile of GO/agar with (a) uniformly and (b) nonuniformly distributed graphene. (c) Maximum and (d) average temperature of graphene embedded agar gel. Temperature distribution along (e) z axis at x=7.5mm for uniformly distribution or x=12.5mm for nonuniformly distribution and (f) x axis at z=1mm.

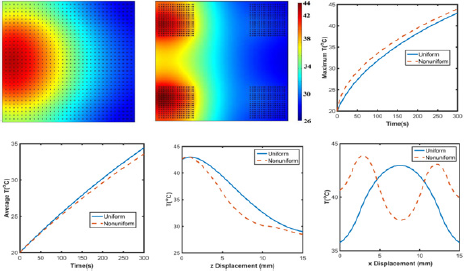
Effects of aggregations: Aggregation is a very common phenomenon in nanomaterials, especially in aqueous solution [34]. Therefore, exploring the effects of aggregation on laser heating behavior is meaningful in both biomedicine and laser welding applications. As shown in Figure 9a-9d, with aggregations, temperature profile greatly differs from the one without aggregations. With uniformly distributed graphene, only one 'heating" island is observed, but there are two 'heating' islands with higher maximum temperature in the hydrogel with nonuniformly distributed GO. Meanwhile, Figure 9e indicates that along the z axis direction, the overall temperature is higher in uniformly distributed GO/agar. Moreover, the surface areas above 30 °C/40 °C in uniformly and non-uniformly distributed GO/agar are 1.76x10‘⁴m²/3.21x10‘ ⁵m² and 1.52x10^-4m²/2.92x10^-5m², suggesting more effective heating occurs when graphene are uniformly distributed.

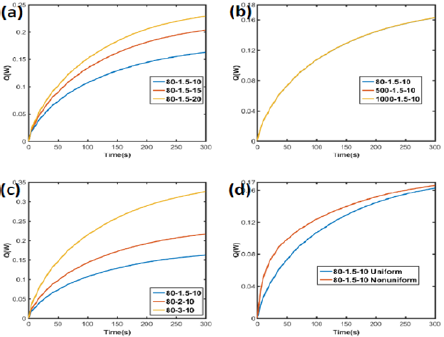
Total heat flux of the surface area was also evaluated as shown in Figure 10. With higher absorption coefficient and power, more heat flux generates in the gel, while thermal conductivity barely affected the total heat flux.

Figure 10: Heat flux of GO/agar with different (a) absorption, (b) thermal conductivity, (c) power and (d) distribution. The legends denoted as thermal conductivity_power_absorption.

Estimated functions

Furthermore, linear and least square methods were used to fit the laser heating model of GO/agar with uniform distribution to estimate a function predicting temperature/heat flux by thermal conductivity, absorption coefficient, power intensity and time.

Firstly, maximum temperature T _max average temperature T_ave and heat flux Q were considered as linear functions of thermal conductivity K∈(80:1000), absorption coefficient α∈(10:55), power intensity P∈(1.5:10) and time t∈(0:300), showing as following:

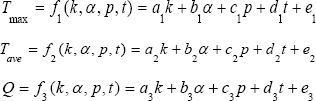
Where, a_i, b_i, c_i, d_i and e_i are the coefficients of thermal conductivity, absorption coefficient, power intensity, time and the constant term.

Least squares method was used to find the minimum of the sum of the squares of the errors S_1,2 and S₃ between the fitting and simulation value [35].

As shown in Equation 13, 14 and 15, thermal conductivity of GO barely affected maximum/average temperature and heat flux. On the other hand, higher absorption results in higher maximum temperature and heat flux, but lower average temperature because of faster light attenuation when α>20cm^-1. Power intensity is the most crucial factor for temperature profile and heat flux, which is linearly proportional to temperature and heat flux, so as time.

According to the fact that only power is approximately linearly correlated to temperature/heat flux, non-linear functions such as quadratic are actually more suitable to predict temperature and heat flux, such as:

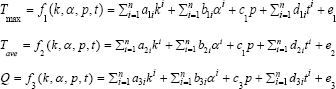
Similarly, least square method (Equation 16-18) was used to obtain the coefficients and constants as shown in Table 2. The accuracy of linear and non-linear estimated equations was compared with the simulation results obtained by COMSOL as shown in Figure 11.

Figure 11: Maximum/average temperature and heat flux with different (a) thermal conductivity, (b) absorption coefficient, (c) power intensity and (d) time.

Table 2: Coefficients and constants in polynomial estimated equations obtained by least square method.

The laser heating effect of GO/agar has been experimentally and theoretically analyzed. Experimental results demonstrate the enhanced photo to thermal conversion of hydrogel embedding with GO, showing an approximate circular temperature distribution, while the simulated results show an approximate semicircular temperature distribution indicating the temperature evolution inside the hydrogel. Moreover, finite element simulation investigated factors including aggregations, absorption coefficient, thermal conductivity and laser power affecting temperature evolution inside GO/agars, providing valuable clues on the control of temperature profile by adjusting these parameters. Due to the small area fraction of GO in hydrogel, thermal conductivity slightly affects temperature profiles, however, absorption coefficient significantly raises the maximum temperature, but probably lowers the average temperature because of laser power attenuation. At 300s, maximum temperature of absorption coefficient 20cm^-1 is greatly higher than the one of absorption coefficient 10cm^{- 1} in x∈(0,6.4mm), but lower in x∈(6.4,15mm) because laser light intensity attenuated faster when absorption is higher. Therefore, materials with proper absorption coefficient should be selected to manipulate penetration 'depth' in biomedical applications. On the other hand, uniformly distributed GO results in higher average temperatures and larger effective heating surface area, but with lower maximum temperature than nonuniformly distributed graphene, so, in laser heating process, uniformly distribution susceptor are always desired to maximize the heating effects. Also, higher laser power intensity increased the temperature overall, however possible heating damage of biological tissue with high laser power intensity may occur. Moreover, estimated functions provided by linear or least square fitting are used to predict maximum temperature, average temperature and heat flux in similar models in the future.

The authors would like to thank Dr. Michelle L. Pantoya and Mr. Evan Vargas for IR camera operations.

1. Su S, Wang J, Wei J, Zaguilan RM, Qiu J, et al. (2015) Efficient photothermal therapy of brain cancer through porphyrin functionalized graphene oxide. New Journal of Chemistry 39(7): 5743-5749.
2. Su S, Wang J, Vargas E, Wei J, Zaguilan RM, et al. (2016) Porphyrin immobilized nanographene oxide for enhanced and targeted photothermal therapy of brain cancer. ACS Biomaterials Science & Engineering 2(8): 1357-1366.
3. Tsang MK, Bai G, Hao J (2015) Stimuli responsive upconversion luminescence nanomaterials and films for various applications. Chemical Society Reviews 44(6): 1585-1607.
4. Yao J, Yang M, Duan Y (2014) Chemistry, biology, and medicine of fluorescent nanomaterials and related systems: new insights into biosensing, bioimaging, genomics, diagnostics, and therapy. Chemical reviews 114(12): 6130-6178.
5. Luz RA, Iost RM, Crespilho FN (2013) Nanomaterials for biosensors and implantable biodevices, in Nanobioelectrochemistry, pp. 27-48.
6. Jaque D, Maestro ML, Rosal B, Gonzalez HP, Benayas A, et al. (2014) Nanoparticles for photothermal therapies. Nanoscale 6(16): 9494-9530.
7. Shi J, Wang L, Zhang J, Ma R, Gao J, et al. (2014) A tumor-targeting near-infrared laser-triggered drug delivery system based on GO@ Ag nanoparticles for chemo-photothermal therapy and X-ray imaging. Biomaterials 35(22): 5847-5861.
8. De Rosa C, Oldani A, Monni M, Terrone A, Garavoglia M (2013) Microwaves assisted liver surgery in elderly patients: technical aspects of our first clinical experience. BMC Surgery 13(1): A14.
9. Rossi F, Micheletti F, Magni G, Pini R, Menabuoni L, et al. (2017) Laser assisted robotic surgery in cornea transplantation. SPIE.
10. Sasidharan A, Sivaram AJ, Retnakumari A, Chandran P, Malarvizhi GL, et al. (2015) Radiofrequency ablation of drug-resistant cancer cells using molecularly targeted carboxyl-functionalized biodegradable graphene. Advanced healthcare materials 4(5): 679-684.
11. Acikgoz H, Mittra R (2016) Suppression of surface currents at microwave frequency using graphene-application to microwave cancer treatment. Applied Computational Electromagnetics Society Journal, 31(6).
12. Vargas E, Pantoya ML, Saed MA, Weeks BL (2016) Advanced susceptors for microwave heating of energetic materials. Materials & Design 90: 4753.
13. Paul A, Narasimhan A, Kahlen FJ, Das SK (2014) Temperature evolution in tissues embedded with large blood vessels during photo-thermal heating. Journal of thermal biology 41: 77-87.
14. Rossi F, Pini R, Menabuoni L (2007) Experimental and model analysis on the temperature dynamics during diode laser welding of the cornea. Journal of Biomedical Optics 12(1): 014031-014031-7.
15. Roberts I, Wang CJ, Esterlein R, Stanford M, Mynors DJ (2009) A threedimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. International Journal of Machine Tools and Manufacture 49(12): 916-923.
16. Patil RB, Yadava V (2007) Finite element analysis of temperature distribution in single metallic powder layer during metal laser sintering. International Journal of Machine Tools and Manufacture 47(7): 10691080.
17. Bourlinos AB, Gournis D, Petridis D, Szabo T, Szeri A, et al. (2003) Graphite oxide: chemical reduction to graphite and surface modification with primary aliphatic amines and amino acids. Langmuir 19(15): 60506055.
18. Nield DA (1991) The limitations of the brinkman-forchheimer equation in modeling flow in a saturated porous medium and at an interface. International Journal of Heat and Fluid Flow 12(3): 269-272.
19. Cai L, White RE (2011) Mathematical modeling of a lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software. Journal of Power Sources 196(14): 5985-5989.
20. Zhao X, Liu ZB, Yan WB, Wu Y, Zhang XL, et al. (2011) Ultrafast carrier dynamics and saturable absorption of solution-processable few-layered graphene oxide. Applied Physics Letters 98(12): 121905.
21. Abahri K, Belarbi R, Trabelsi A (2011) Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials. Building and Environment 46(7): 1354-1360.
22. Zhang X, Gao Y, Hu M (2016) Robustly engineering thermal conductivity of bilayer graphene by interlayer bonding. Scientific report 6.
23. Zhang M, Che Z, Chen J, Zhao H, Yang L, et al. (2010) Experimental determination of thermal conductivity of water-agar gel at different concentrations and temperatures. Journal of Chemical & Engineering Data 56(4): 859-864.
24. Koo J, Kleinstreuer C (2005) Impact analysis of nanoparticle motion mechanisms on the thermal conductivity of nanofluids. International Communications in Heat and Mass Transfer 32(9): 1111-1118.
25. Dikin DA, Stankovich S, Zimney EJ, Piner RD, Dommett GH, et al. (2007) Preparation and characterization of graphene oxide paper. Nature 448(7152): 457-460.
26. Markovic ZM, Trajkovic HLM, Markovic TBM, Kepic DP, Arsikin KM (2011) In vitro comparison of the photothermal anticancer activity of graphene nanoparticles and carbon nanotubes. Biomaterials 32(4): 1121-1129.
27. Wong I, Atsumi S, Huang WC, Wu TY, Hanai T, et al. (2010) An agar gel membrane-PDMS hybrid microfluidic device for long term single cell dynamic study. Lab on a Chip 10(20): 2710-2719.
28. Lee D, Huang W (1996) Enthalpy-entropy compensation in micellization of sodium dodecyl sulphate in water/methanol, water/ethylene glycol and water/glycerol binary mixtures. Colloid & Polymer Science 274(2): 160-165.
29. Viswanath DS, Ghosh T, Prasad DHL, Dutt NVK, Rani KY (2007) Introduction, in Viscosity of Liquids. Springer p. 1-8.
30. Balandin AA (2011) Thermal properties of graphene and nanostructured carbon materials. Nature materials 10(8): 569-581.
31. Su R, Lin SF, Chen DQ, Chen GH (2014) Study on the absorption coefficient of reduced graphene oxide dispersion. The Journal of Physical Chemistry C 118(23): 12520-12525.
32. Shen J, Zhu Y, Yang X, Zong J, Zhang J, et al. (2012) One-pot hydrothermal synthesis of graphene quantum dots surface-passivated by polyethylene glycol and their photoelectric conversion under near-infrared light. New Journal of Chemistry 36(1): 97-101.
33. Qu D, Zheng M, Du P, Zhou Y, Zhang L, et al. (2013) Highly luminescent S, N co-doped graphene quantum dots with broad visible absorption bands for visible light photocatalysts. Nanoscale 5(24): 12272-12277.
34. Hotze EM, Phenrat T, Lowry GV (2010) Nanoparticle aggregation: challenges to understanding transport and reactivity in the environment. Journal of environmental quality 39(6): 1909-1924.
35. Ramsey JB (1969) Tests for specification errors in classical linear least- squares regression analysis. Journal of the Royal Statistical Society. Series B (Methodological) p. 350-371.