Entropic Equation of the Condition of Simple Crystal Material

In the usual thermal equation of state of a one-component substance (for example, the equation of Clapeyron-Mendeleev) from the standard four thermodynamic parameters are three: the pressure p, volume V and temperature T. It is essential that the condensed states (crystalline, amorphous and liquid) differ greatly in the degree of ordering of the atomic structure, so for them is more important than pressure may be the fourth parameter, the entropy S, which is not included in the normal equation of state .

The desired relationship can be deduced from the general statistical definition of entropy:

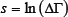
where is the statistical weight of the state [1].

In quasi classical approximation is determined by the relation

∆p∆q -phase volume, s-the number of degrees of freedom.

In the single-particle approximation s=3, so that the statistical weight can be considered as the ratio of two quantities having the dimension of volume:

The last relation can be represented in the form

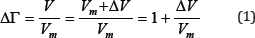
V is the total effective volume in which a particle can actually exist, the value Vm has the meaning of the minimum volume in which the particle can be localized under given conditions, AV is the additional volume to the minimum. Then

The expression for the parameter V_m in the general case should be sought by solving the corresponding quantum-mechanical problem. However, the solution of the problem can be approached in another way.

In principle, the most general formulas for calculating the thermodynamic functions of a substance in different aggregate states should have the same structure,

since the fundamental nature of the interatomic interaction does not change under the aggregate transformation. With this in mind, we consider the Sakura-Tetrode equation for an ideal gas:

The parameter α contains only constants and the mass of the atom, i.e. is a material constant.

The combination of the quantities in [2] is 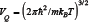called the "quantum volume". The physical meaning of the "quantum volume": the volume of the cube with a side approximately equal to the thermal mean of the de Broglie wavelength of a particle of mass m. Thus, the value V_m can be put equal to the "quantum volume", at least in order of magnitude.

From the presence of the temperature in (5) follows: at T→0,V_ m→0,S→0.

Substituting (5) into (2) gives:

In ideal gas molecules uniformly "use" all volume provided to them. In crystals the atoms spend most of the time near equilibrium positions at lattice, so that only part of the volume, determined by the magnitude of the amplitude of the thermal oscillations, is effectively used. In real crystals, up to the melting point, the relative rms amplitude of the thermal oscillations has sufficiently small values, which makes it possible to determine the "effectively used volume" in the first approximation as the volume of a sphere with a radius equal to σ-r₀

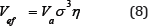
where r₀ is the minimum interatomic distance, and the packing ratio for a given type of lattice is introduced to account for the deviation of the shape of the unit cell from the spherical one.

Replacing in (7) V_a on v_of and accepted V_m on (5), we will receive the equation

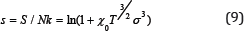
in which x₀ -a constant, determined by the sort of substance,

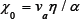
In spite ofthe fact that only known quantities enter into formulas for calculating the parameter x_o, it is advisable to consider it as an adjustable parameter (of the Debye frequency type) and to find it on the basis of experimental data.

Formula (9) with (8) connects the three thermodynamic parameters: temperature, volume and entropy and can therefore be considered as the equation of state. In contrast to known thermal and caloric, this equation should be called entropic [3,4].

Entropy is usually calculated from the experimental data on the heat capacity. The temperature dependences of the heat capacity of simple substances have been experimentally determined with relatively high accuracy practically throughout the entire range of existence of the condensed states. At the same time, the experimental data on the amplitudes of thermal vibrations of atoms are much less precise and extremely limited. Therefore, it is more convenient to test the formula (9), calculating a parameter a based on entropy data, and not vice versa.

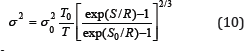
Where σ²₀ is the value of the disorder parameter at a certain temperature T₀ and the corresponding value of the entropy σ₀. If the value of a is known, then relation (10) makes it possible to calculate the temperature dependence of the parameter a in absolute units.

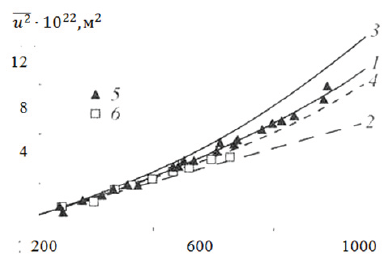
In Figure 1 for example shows the temperature dependence of disorder parameter σ² of platinum, derived from data on entropy and calculated by the formula (10). The calculation of the entropy was carried out on the data of heat capacity given in [5]. As can be seen, the data calculated in this way are in good agreement with experiment much better than that calculated by other models.

Similar calculations were carried out for a wide range of simple crystalline substances and inorganic compounds using data on the entropy and the heat capacity from [5].

The calculations showed that the temperature dependence of the disorder parameter (the amplitude of thermal vibrations) for most of the chemical elements in the crystalline state with sufficient precision is interpolated by a polynomial of second degree. It was also found that the free term in the polynomial does not vanish for any substance, and its value close to the amplitude of zero-point oscillations.

Thus, despite the relative roughness ofthe approximations used, the entropy equation of state obtained describes the temperature dependence of the entropy of simple crystals quite well, connecting it with the amplitude of the thermal vibrations of the atoms.

Figure 1 dependence u^-2 in Cu on temperature: 1-calculation according to formula (9), 2-according to Debye theory, 3 and 4 -calculation of a harmonic and quasi-harmonic, respectively, according to [4], 5 and 6-experimental data [4] and [5] respectively.

1. Landau LD, Lifshiz EM (2002) Statistical physics, Moscow, p. 39.
2. Kittel C (1997) Statistical thermodynamics. Moscow, p. 142.
3. (1978) Thermodynamic properties of individual substances, Moscow.
4. Martin CJ, O Connor DA (1997) J Phys C: Solid State Phys, 10, 3521.
5. Gupta OP (1983) Temperature dependence of the anharmonic debye- waller factor for cubic metal. J Phys Soc Jap 52, 4237-4247.