Improving the Accuracy of a Widely used Approximation for Computing the Faddeyeva and Voigt Functions

Because of its applications in many fields of physics such as atmospheric radiative transfer, plasma spectroscopy, nuclear physics, nuclear magnetic resonance, etc, the analysis and evaluation of the complex probability function, commonly known as the Faddeyeva function, has gained a wide interest in the literature [1-18]. The function is defined mathematically as the scaled complementary error function for a complex variable and can, therefore, be expressed as,

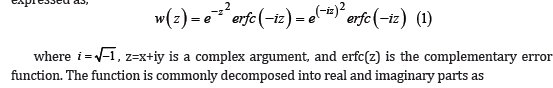
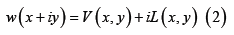
where V and L are known as the real and imaginary “Voigt functions,” since V(x,y) is the Voigt line profile, used in spectroscopy and radiative transfer, ressulting from the convolution of the Gaussian profile (as a result of Doppler broadening) and a Lorentzian profile (result of pressure or collision broadening). The imaginary Voigt function L is also useful for various applications and needs to be taken into consideration as well. The fact that a closed form expression does not exist for the convolution integral defining the Voigt functions or for the closely related Faddeyeva function led to the development of a wide variety of algorithms to numerically evaluate the functions. These algorithms vary significantly in their accuracy and computational speed and the decision for a certain algorithm will depend on the particular application under consideration. One of the algorithms widely employed in the solution of practical problems requiring numerous evaluation of the complex probability function is the Humlíček’s w4 algorithm [6]. The algorithm is efficient for some applications tolerating low accuracy computations (10^-4), however, as shown in the literature (see for example [11,18]) the w4 algorithm does suffer from a loss of its claimed accuracy near the real axis. It is also worth mentioning that Humlíček’s w4 algorithm is the basis of several other refinements (see for example [10-12,16,17]). In most of these references, Humlíček’s w4 algorithm is shown to be remarkably more efficient when the parameter x is a vector while y is a scalar. Even though, a brief survey and benchmarking tests by Schreier [17] considering practical aspects of Fortran and Python implementations demonstrated that programming language, compiler choice, and implementation details influence computational speed and that there is no unique ranking of algorithms. In this note we provide a simple reform to this problem where the reformed algorithm maintains the claimed accuracy of the algorithm over the whole domain of interest.

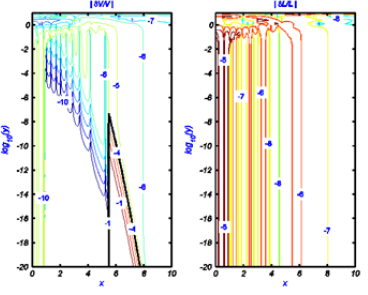
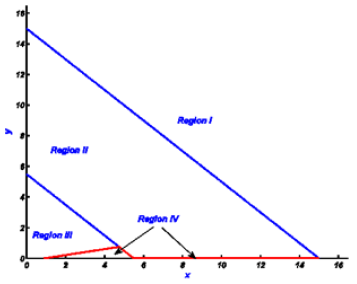
In Humlíček’s w4 algorithm, the x-y plane is divided into four regions where for each region an approximate expression is used in the form of a rational polynomial. The four regions used in the w4 algorithm are shown in (Figure 1). The borders for these regions are also summarized in the second column of (Table 1) below. The w4 algorithm calculates both the real and imaginary parts of the Faddeyeva function concurrently. A thorough investigation of the accuracy of the w4 code over all of its four regions, using algorithm-916 [18] as a reference, shows that the accuracy failure of the w4 code occurs for values of y<10^-7 and values of x in Region II. (Figure 2) shows contour plots of the common logarithm (base 10) of the absolute values of the relative error, in the calculation of the real and imaginary parts of the Faddeyeva function, resulting from using the w4 algorithm with algorithm-916 [18] as a reference. As pointed out by Garcia [13] the damping parameter y, for the Lyman transitions of intergalactic HI spans a range of 9.3×10^-9 (corresponding to higher order Lyman transitions) to 6.5×10^-4 (corresponding to Lyα). Accordingly, this region in which the w4 algorithm loses its claimed accuracy is of practical interest to some applications.

Figure 1:The four regions in the x-y plane in the Humlíček’s original algorithm.

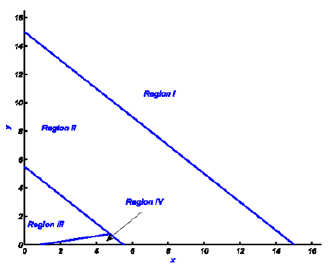
Table 1: Borders of the four regions in Humlíček’s original and reformed algorithms.

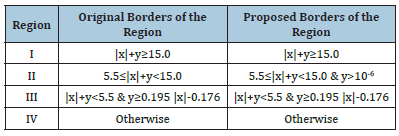
Figure 2: Contour plots of the absolute relative error resulting from using the w4 algorithm for calculating the real and imaginary parts of the Faddeyeva function with algorithm-916 [18] as a reference. The thick line in the left part shows the contour of relative error equals 10-4 where the region inside this contour is the region where Humlíček’s original algorithm loses its claimed accuracy.

Figure 3: The new four regions in the x-y plane in the Humlíček’s reformed algorithm.

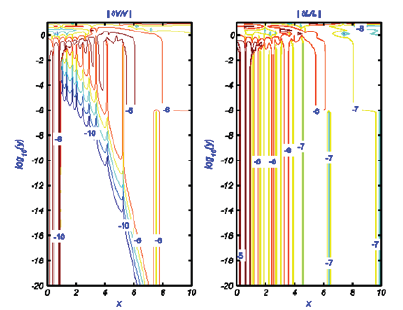
the w4 algorithm near the x-axis exists in redefining the borders of one of the regions in the partitioning used in the original routine. The approximation proposed by Humlíček to be used in Region IV in the w4 algorithm is found to be very accurate for very small values of y. We propose using this expression for y≤10^-6 and 5.5≤|x|+y<15.0 to overcome the loss-of-accuracy problem near the real axis. This means that Region IV will be extended to include this part of Region II as schematically shown in (Figure 3). The borders of the modified regions are given in the third column of (Table 1) where a simple modification of the borders of Region II is shown in boldface letters. This is a very simple and minor coding change to the original w4 algorithm that can be straightforwardly implemented to fix the above-mentioned accuracy problem in such a widely used algorithm. (Figure 4) shows contour plots similar to those in (Figure 2) but for results from using the reformed w4 algorithm where, as it can be seen, the claimed accuracy of the w4 algorithm is restored and the loss-of-accuracy problem is removed. (Figure 4) Contour plots of the common logarithm (base 10) of the absolute of the relative error resulting from using the reformed w4 algorithm for calculating the real and imaginary parts of the Faddeyeva function with algorithm-916 [18] as a reference.

Figure 4: Contour plots of the common logarithm.

A simple reform for treating the reported problem of lossof- accuracy near the real axis of Humlíček’s w4 algorithm is introduced. The reformed routine maintains the claimed accuracy of the algorithm over a wide and fine grid that covers all regions of interest.

1. Faddeyeva VN, Terentev NM (1961) Tables of values of the function for complex argument. In: Gosud, Izdat (eds.), The Teor Lit. Elsevier Publishers, UK, pp. 1-288.
2. Young C (1965) Calculation of the absorption coefficient for lines with combined doppler and lorentz broadening. J Quant Spectrosc Radiat Transfer 5(3): 549-552.
3. Armstrong BH (1967) Spectrum line profiles: The voigt function. J Quant Spectrosc Radiat Transfer 7(1): 61-88.
4. Gautschi W (1970) Efficient computation of the complex error function. SIAM J Numer Anal 7(1): 187-198.
5. Hui AK, Armstrong BH, Wray AA (1978) Rapid computation of the voigt and complex error functions. J Quant Spectrosc Radiat Transfer 19(5): 509-516.
6. Humlíček J (1982) Optimized computation of the voigt and complex probability functions. J Quant Spectrosc Radiat Transfer 27(4): 437-444.
7. Poppe GPM, Wijers CMJ (1990) Algorithm 680: Evaluation of the complex error function. ACM Transactions on Mathematical Software 16(1): 1.
8. Schreier F (1992) The voigt and complex error function: A comparison of computational methods. J Quant Spectrosc Radiat Transfer 48(5/6): 743-762.
9. Weideman JAC (1994) Computation of the Complex Error Function. SIAM J Numer Anal 31(5): 1497-1518.
10. Kuntz M (1997) A new implementation of the humlicek algorithm for the calculation of the voigt profile function. J Quant Spectrosc Radiat Transfer 57(6): 819-824.
11. Wells RJ (1999) Rapid approximation to the voigt/faddeeva function and its derivatives. J Quant Spectrosc Radiat Transfer 62(1): 29-48.
12. Ruyten W (2004) Comment on “A new implementation of the Humlicek algorithm for the calculation of the voigt profile function” by M. Kuntz [JQSRT 57(6)(1997) 819-824]. J Quant Spectrosc Radiat Transfer 86(2): 231-233.
13. Garcia TT (2006) Voigt profile fitting to quasar absorption lines: An analytic approximation to the voigt-hjerting function. Mon Not R Astron Soc 369(4): 2025-2035.
14. Letchworth KL, Benner DC (2007) Rapid and accurate calculation of the voigt function. J Quant Spectrosc Radiat Transfer 107(1): 173-192.
15. Abrarov SM, Quine BM, Jagpal RK (2010) Rapidly convergent series for high-accuracy calculation of the voigt function. J Quant Spectrosc Radiat Transfer 111(3): 372-375.
16. Imai K, Sizuki M, Takahashi C (2010) Evaluation of Voigt algorithms for the ISS/JEM/SMILES L2 data processing system. Advances in Space Research 45(1): 669-675.
17. Schreier F (2011) Optimized implementations of rational approximations for the voigt and complex error function. J Quant Spectrosc Radiat Transfer 112(2): 1010-1025.
18. Zaghloul MR, Ali AN (2011) Algorithm 916: Computing the faddeyeva and voigt functions. ACM Trans Math Software 38(2): 1-22.