Open Journal of Cardiology & Heart Diseases

Study of Dynamics of Some Human Diseases on the Base of Fractal Approach (“Range” Method)

Oksengendler BL¹*, Ivanov NV², Ashirmetov A Kh³, Im VK⁴ and Maksimov SE¹

¹Institute of Chemistry and Physics of Polymers, Academy of Science of the Republic of Uzbekistan, Uzbekistan

²North-Western Medical Academy of Russia, Russia

³Institute of Hematology of Ministry of Health of the Republic of Uzbekistan, Uzbekistan

⁴Institute of Heart Surgery of Ministry of Health of the Republic of Uzbekistan, Uzbekistan

*Corresponding author: Boris L Oksengendler, Institute of Chemistry and Physics of Polymers, Academy of Science of the Republic of Uzbekistan; 100128, Tashkent, A. Kadyri Str 7b, Uzbekistan

Submission: September 01, 2017; Published: December 18, 2017

DOI: 10.31031/OJCHD.2017.01.000504

ISSN: 2578-0204
Volume1 Issue1

Keywords: Fractal; “Range” method; Cardiology; Oncology; Diabetology

The last quarter of the 20^th century clearly demonstrated the victorious introduction of the ideas of synergetics and nonlinear dynamics to biology and medicine. This applies to cardiology, to physiology of the brain, to ophthalmology, orthopedics, diabetes and to oncology [1]. Practice showed that from the many methods which are characteristic for the synergetics and nonlinear dynamics, the following ones have been most appreciated: the approach of non-linear differential equations (Poincare), catastrophe theory (see [2]), fractal geometry [3]. In present time with the large generality, it is possible to relate large hopes specifically to fractal methodology, which is able to analyze both structurally geometric and structurally temporal regularities of disease processes. It is very interesting to note the uniformity of such an analysis in the aspect of the so-called fractal "range" method proposed by Hurst [4] for the purely technical problem of the prefractal period.

This approach uses the following values:

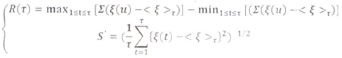
where ξ(t) are the peaks of physiological indices.

Let us demonstrate here the applicability of this approach to the dynamics of various diseases.

Cardiology

The variability of the heart rhythm discovered long time ago as a result of Goldberder [1] and others revealed some fundamentally new aspects. It was shown that the heart rhythms of healthy people contain a certain proportion of both order and chaos, and the limiting situations (both complete order and complete chaos) are lethal. The identification of fraction of the order and chaos turned out to be particularly convenient in the language of the Poincare sections. In the most general terms, it turned out that the variability of the heart rhythm reflects both the work of the cardiovascular system and the work of the mechanisms of regulation of the whole organism. We also want to mention here the possibility of study of the evolution of variability by the Hurst method mentioned above, which is much less laborious in calculations, but the specific interpretation of which is just beginning for this problem. We will start from the analysis of the data set for the sequential series of R-R intervals on the ECG. Suppose that the set of these intervals corresponds to the so-called generalized Brownian motion of Mandelbrot, which corresponds to the Hurst exponent 0<H<1 [4], i.e. if the "R-R interval" is the X(t) generalized random function, then X(t)-X(t₀)~ ξ|t-t₀|^H, (t>t₀), where t and t₀ are any pair of points in time. By changing X(t) to B_H(t ) we obtain for the dispersion <[B_H(t)-B_H(t₀)]²>~[t-t₀]^2H. Then for correlation functions of future increments B_H(t) with past B_H(-t) it is possible to obtain C(t)=2^(2H-1)-1. Since B_H(Δt)~|Δt|^H, we can show the following: R(τ)/ S~τ^h, where S is the dispersion and R(τ) is the delay amplitude; note, that the knowledge of H allows to obtain the fractal dimension of dynamical curve.

Oncology

The use of fractal ideas in oncologists has been carried out up to now in two ways: by analyzing of the modification of the geometric structure of healthy object after the disease, or by bioinformation analysis of the genes of sick people [5]. However, another option is possible, namely, the use of the fractal method of "range" showing the dynamics of the oncological process. An interesting example is the detected fact of the change of the ratio of concentrations of small and large fragments of extracellular DNA as the oncological process deepens. Introducing the value of γ(τ)=N₁₀₀/N₄₀₀, we trace the changes of γ(τ) from the onset of the oncological process to the time equal to τ (here 100 and 400 correspond to single-stranded DNA with lengths of 100 bp and 400 bp). Before the beginning of the process γ=1, in the oncological process γ(τ) increases, nevertheless, it demonstrates the character of the fractal curve. We will analyze the magnitude of the "range" of γ(τ) divided by the standard deviation S, that is, the square root of the dispersion, and tracing this ratio as the function of time τ we obtain the Hurst dependence R/S~(τ/2)^H.

Diabetology

Not so long ago, the so-called glucose variability was discovered at different values of the fragmentation of the time scale [6]. As a result of vigorous discussion it became clear that small- scale oscillations have a substantially different nature (different biochemistry) than large-scale fluctuations in sugar concentration over time. Among the various approaches to somehow discuss the metric of this phenomenon, it was possible to dwell on the ideas of nonlinear dynamics; in particular, conceptions of the amplitudes of sugar oscillations and timings [6] were introduced. The problem of risk was described in this case very laboriously, to reduce it somehow to the approach of Kovachev B [6]. The use of the fractal approach of "range" promises much greater clarity in the problem of risk. Let us investigate the time dependence of the glucose concentration, which is fractal in nature, within the frameworks of the idea of "range". So, during the observation time τ we can write the expression R(τ)/S(τ), where R is the difference between the maximum τ minimum value of the glycotic curve during τ and S(τ) the dispersion for the same time. The application of this ideology to numerous patients also demonstrated here the Hurst dependence R/S~(τ/2)^H.

For all three examples it can be assumed uniformly that the regimes with H=1/2 correspond to independent random changes in the characteristics of parameters for all types of diseases. In particular, for all biochemical reactions underlying in the base of the pathological processes we have the following. If H>1/2, then this indicates on the increase of pathological processes and, roughly speaking, the system goes to the its destruction (persistent mode), when the previous increments stimulate the subsequent ones. If H<1/2, then the previous increment stimulates the decrease in subsequent increments (antipersistent mode). Thus, the case H>1/2 corresponds to a greater risk for the development of the pathological process. Obviously, on the basis of monitoring of the change of H value, one can monitor the effectiveness of the medical treatment.

1. Havlin S, Buuldyrev SV, Goldberger AL, Mantegna RN, Ossadnik SM, et al. (1995) Fractals in biology and medicine. 6: 171-201.
2. Malinetsky GG (2009) Matematical basis of synergetics. (6^th edn), Librokom, Moscow, Russia, p. 312.
3. Mandelbrot BB (1977) Fractals: Form, Change and Dinention. WH Freeman, San Francisco, USA, p. 260.
4. Hurst HE (1951) Long-term storage capacity of reservoirs. Trans Am Soc Civ Eng 116(1): 770-808.
5. Oksengendler BL, Ashirmetov A Kh (2017) About possibility of the use of DNA sorbtion processes on fractal surface with the diagnostic purposes in medicine. LIPNPI School on condensed state physics (CSP- 2017), p. 16.
6. Kovachev B (2017) Assessment of risk for severe hypoglycemia among DNA validation of the low blood glucose index. Diabetes Care 21: 18701875.