- Submissions

Full Text
Open Access Biostatistics & Bioinformatics
Inverse Transient Thermoelastic Problems of Semi- Infinite Hollow Cylinder on Outer Curved Surface
Pallavi Meshram and NW Khobragade*
Department of Mathematics, RTM Nagpur University, India
*Corresponding author: NW Khobragade, Department of Mathematics, RTM Nagpur University, Nagpur (MS), India
Submission: March 24, 2018;Published: April 02, 2018

ISSN: 2578-0247Volume1 Issue3
Abstract
This paper is concerned with inverse transient thermoelastic problem of semi-infinite hollow cylinder in which we need to determine the temperature distribution, unknown temperature gradient, displacement function and thermal stresses when the boundary conditions are known. Integral transform techniques are used to obtain the solution of the problem. The results are obtained in terms of Bessel’s function in the form of infinite series.
Keywords: Semi-infinite hollow cylinder; Transient problem; Integral transform; Inverse problem
Introduction
In 1962, Nowacki [1] has published a book on thermoelasticity. Sierakowski & Sun [2] studied the direct problems of an exact solution to the elastic deformation of finite length hollow cylinder. In 2009, Kamdi et al. [3] studied transient thermoelastic problem for a circular solid cylinder with radiation. Walde & Khobragade [4] discussed transient thermoelastic problem of a finite length hollow cylinder. Khobragade et al. [5] derived thermal stresses of a finite length hollow cylinder. Warbhe & Khobragade [6] discussed numerical study of transient thermoelastic problem of a finite length hollow cylinder. Lamba & Khobragade [7] studied analysis of coupled thermal stresses in axisymmetric hollow cylinder. Hiranwar & Khobragade [8] studied thermoelastic problem of a cylinder with internal heat sources. Bagde & Khobragade [9] discussed heat conduction problem for a finite elliptic cylinder.
Khobragade et al. [10] investigated thermal deflection of a finite length hollow cylinder due to heat generation. Khobragade [11] studied thermoelastic analysis of a thick hollow cylinder with radiation conditions. Ghume et al. [12] derived interior thermo elastic solution of a hollow cylinder. Chauthale et al. [13] studied thermal stress analysis of a thick hollow cylinder. Singru & Khobragade [14] developed integral transform methods for inverse problem of heat conduction with known boundary of semi-infinite hollow cylinder and its stresses. Fule et al. [15] derived thermal stresses of semi-infinite hollow cylinder with internal heat source. Ghaleb et al. [16] studied a problem of plane, uncoupled linear thermoelasticity for an infinite, elliptical cylinder by a Boundary Integral Method. Dhaba et al. [17] discussed deformation for a rectangle by a finite Fourier transform. Dhaba & Abou-Dina [18] derived thermal stresses induced by a variable heat source in a rectangle and variable pressure at its boundary by finite Fourier transform. In this paper, an attempt has been made to solve two inverse problems of thermoelasticity. In both the problems, an attempt has been made to determine the temperature distribution, unknown temperature gradient, displacement function and thermal stresses on outer curved surface of semi-infinite hollow cylinder.
Statement of the Problem-I
Consider semi-infinite hollow cylinder occupying the space D:
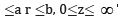 The thermoelastic displacement function as 1
is governed by the Poisson’s equation
The thermoelastic displacement function as 1
is governed by the Poisson’s equation
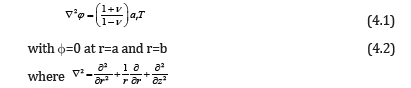
and at are the Poisson’s ratio and the linear coefficient of thermal expansion of the material of the cylinder and T is the temperature of the cylinder satisfying the differential equation

Subject to the initial conditions

The boundary conditions
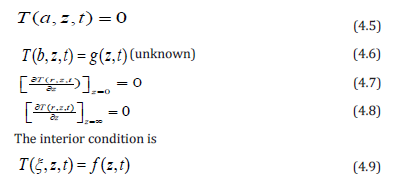
Where k is the thermal diffusivity of the material of the cylinder The radial and axial displacement U and W satisfying the uncoupled thermoelastic equations as [2] are
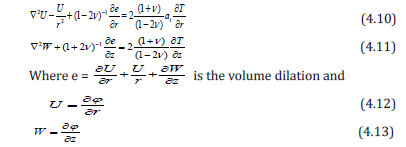
The stress functions are given by
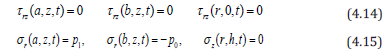
where p1 and p0 are the surface pressures assumed to be uniform over the boundaries of the cylinder. The stress functions are expressed in terms of the displacement components by the following relations:
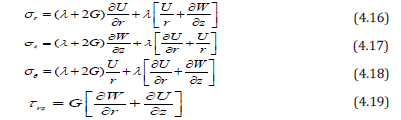
where  is Lame’s constant, G is the shear modulus
and U and W are the displacement components. Equations (4.1)
to (4.19) constitute the mathematical formulation of the problem
under consideration.
is Lame’s constant, G is the shear modulus
and U and W are the displacement components. Equations (4.1)
to (4.19) constitute the mathematical formulation of the problem
under consideration.
Solution of the Problem
Applying Fourier cosine transform to the equations (4.3), (4.4), (4.5), (4.6), (4.9) and using the conditions (4.7), (4.8) one obtains

where T denotes Fourier cosine transform of T and n is Fourier cosine transform parameter,
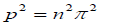
Applying Laplace transform to the equations (5.1), (5.3), (5.4), (5.5) and using the condition (5.2) one obtains

where T∗ denotes Laplace transform of T and s is Laplace transform parameter.
The equation (5.6) is a Bessel’s equation whose gives
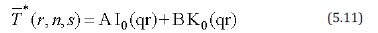
Where A, B are constants and I0, K0 are modified Bessel’s functions of first and second kind of order zero respectively.
Using (5.8) and (5.10) in (5.11) one obtains

Solving (5.12) and (5.13) one obtains
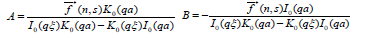
Substituting the values of A and B in equation (5.11) and using condition (5.9) one obtains
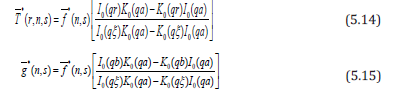
Applying Inverse Laplace transform to the equation (5.14) one obtains
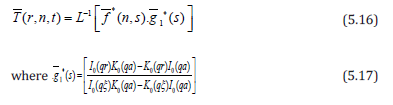
To Calculate the Inverse Laplace Transform of (5.17):
Applying inverse Laplace transform to the equation (5.17) one obtains
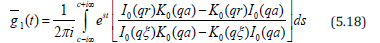
Where c is greater than the real part of the singularities of the integrand
The integrand is a single valued function of s. The poles of the integrand are at the points

Where λm are the positive roots of the transcendental equation
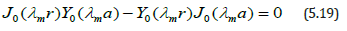
The zeros of 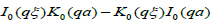 are all real
and simple.
are all real
and simple.
The poles of the integrand (5.18) are at 
Using the contour of Figure 1,
Figure 1:
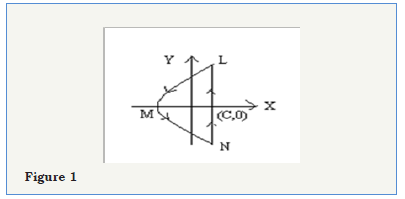
The integral (5.18) is equal to 2i times the sum of the residues at the poles of the integrand.
To find the residue at the point, one requires the result:

Equation (5.20) reduces to the form

Using (5.20) and (5.22) in (5.18) one obtains

Applying convolution theorem to the equation (5.16) one obtains
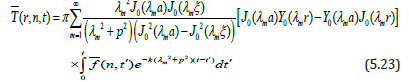
Applying inverse Fourier cosine transform to the equation (5.23) we obtain
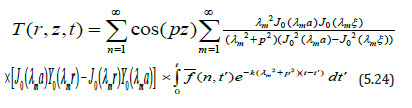
Where m, n are positive integers
Applying inverse Laplace transform and then inverse Fourier cosine transform to the equation (5.15) one obtains the expression for unknown temperature gradient g(z,t) as

where m, n are positive integers, m are the positive roots of the transcendental equation

Determination of Thermoelastic Displacement
Substituting the value of temperature distribution T(r,z,t) from equation (5.24) in equation (5.1), one obtains the thermoelastic displacement function (r, z, t) as

Using the value of thermoelastic displacement function from equation (6.1) in equations (4.12) and (4.13) one obtains the radial and axial displacement U and W as
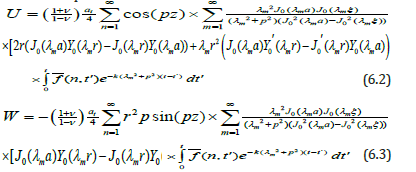
Determination of Stress Functions
Using the values of radial and axial displacement from equations (6.2) and (6.3) respectively in equations (4.16), (4.17), (4.18) and (2.19), the stress functions are obtained as
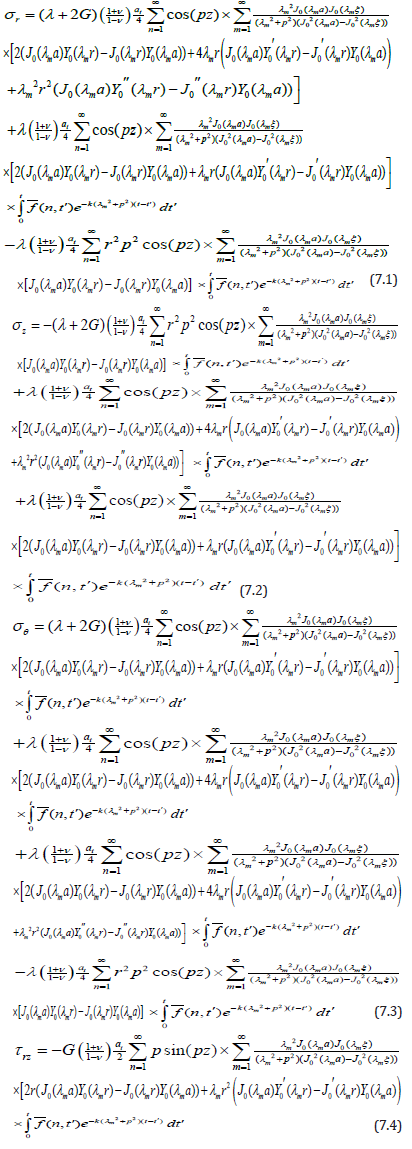
Special Case

Applying Fourier cosine transform to the equation (8.1) one obtains

Substituting the value of f (n, t) from equation (8.2) in the equations (5.24) and (5.25) one obtains
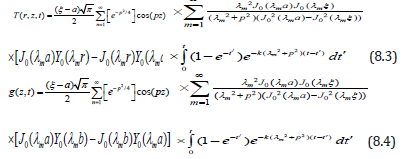
Numerical Results
Set 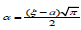 , a=1m, b=2m, =1.5m, t=1sec, k=0.86 and m
are the roots of the transcendental equation
, a=1m, b=2m, =1.5m, t=1sec, k=0.86 and m
are the roots of the transcendental equation
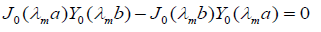
as [3] in equation (9.4) one obtains (Figure 2)
Figure 2:

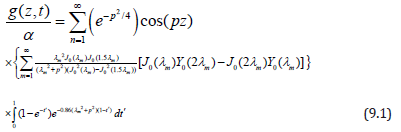
Statement of the Problem-II
Consider semi-infinite hollow cylinder occupying the space D:
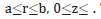 . The thermoelastic displacement function as 1 is
governed by the Poisson’s equation
. The thermoelastic displacement function as 1 is
governed by the Poisson’s equation
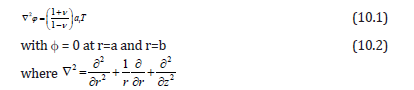
and at are the Poisson’s ratio and the linear coefficient of thermal expansion of the material of the cylinder and T is the temperature of the cylinder satisfying the differential equation

The boundary conditions are

where k is the thermal diffusivity of the material of the cylinder.
The radial and axial displacement U and W satisfying the uncoupled thermoelastic equations as [2] are
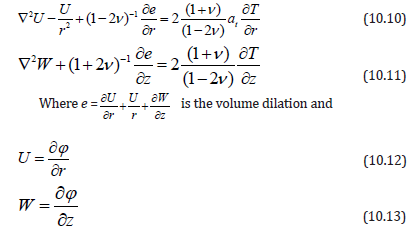
The stress functions are given by
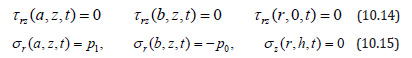
Where p1 and p0 are the surface pressures assumed to be uniform over the boundaries of the cylinder. The stress functions are expressed in terms of the displacement components by the following relations:

where 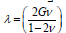 is Lame’s constant, G is the shear modulus
and U and W are the displacement components. Equations (10.1)
to (10.19) constitute the mathematical formulation of the problem
under consideration.
is Lame’s constant, G is the shear modulus
and U and W are the displacement components. Equations (10.1)
to (10.19) constitute the mathematical formulation of the problem
under consideration.
Solution of the Problem
Applying Fourier cosine transform to the equations (10.3), (10.4), (10.5), (10.6), (10.9) and using equations (10.7), (10.8) one obtains
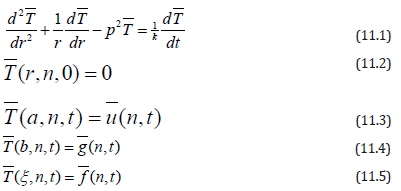
where T denotes Fourier cosine transform of T and n is Fourier cosine transform parameter.
The equation (11.6) is a Bessel’s equation whose solution gives
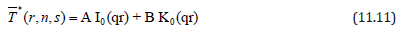
Where A, B are constants and I0, K0 are modified Bessel’s functions of first and second kind of order zero respectively.
Using equations (11.8) and (11.10) in equation (11.11) we get

Solving equations (11.12) and (11.13) we obtain
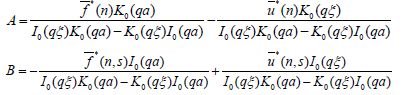
Substituting the values of A and B in equation (11.11) and using condition (11.9) one obtains

Applying Inverse Laplace transform and inverse Fourier cosine transform to the equation (11.14) and using equation (10.6) one obtain the expressions for the temperature distribution T(r,z,t) and unknown temperature gradient g(z,t) as
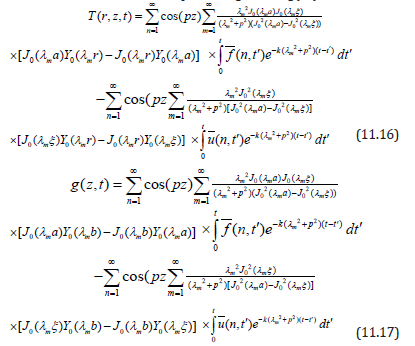
where m, n are positive integers, m are the positive roots of the transcendental equation
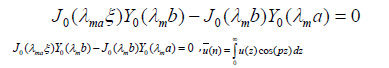
Determination of Thermoelastic Displacement Function
Substituting the value of temperature distribution T(r,z,t) from equation (11.14) in equation (10.1), one obtains the expression for thermoelastic displacement function (r, z,t) as

Using the value of thermoelastic displacement function (r, z,t) from equation (12.1) in equations (10.12) and (10.13) one obtains the radial and axial displacement U and W as

Determination of Stress Functions
Using the values of radial and axial displacement U and W from equations (12.2) and (12.3) in equations (10.16), (10.17), (10.18) and (10.19), the stress functions are obtained as

Special Case
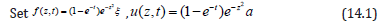
Applying Fourier cosine transform to the equation (12.1) one obtains

Figure 3:


Conclusion
In this section, we derived the expressions of temperature distribution, unknown temperature gradient, displacement function and thermal stresses of semi-infinite hollow cylinder on outer curved surface, when the boundary conditions are known. The Fourier cosine transform and Laplace transform techniques are used to obtain the numerical results. The solutions are obtained in terms of Bessel’s function in the form of infinite series and depicted graphically. The behaviors of graphs are of sinusoidal nature. The results that are obtained can be applied to the design of useful structures or machines in engineering applications. Any particular case of special interest can be derived by assigning suitable values to the parameters and functions in the expressions.
Acknowledgement
Authors are thankful to anonymous referee for his useful suggestions.
References
- Nowacki W (1962) Thermoelasticity. Mass Addition-Wesley Pub Co.
- Sierakowski RL, Sun CT (1968) An exact solution to the elastic deformation of a finite length hollow cylinder. Journal of the Franklin Institute 286(2): 99-113.
- Kamdi DB, Khobragade NW, Durge MH (2009) Transient thermoelastic problem for a circular solid cylinder with radiation. Int Journal of Pure and Applied Maths 54(3): 387-406.
- Walde RT, Khobragade NW (2012) Transient thermoelastic problem of a finite length hollow cylinder. Canadian Journal on Science and Engg Mathematics Research 3(2): 56-60.
- Ashwini AK, Khobragade NW (2012) Thermal stresses of a finite length hollow cylinder. Canadian Journal on Science and Engg. Mathematics Research 3(2): 52-55.
- Warbhe MS, Khobragade NW (2012) Numerical study of transient thermoelastic problem of a finite length hollow cylinder. Int Journal of Latest Trends in Maths 2(1): 4-9.
- Lamba NK, Khobragade NW (2011) Analysis of coupled thermal stresses in a axisymmetric hollow cylinder. Int Journal of Latest Trends in Maths 1(2).
- Hiranwar PC, Khobragade NW (2012) Thermoelastic problem of a cylinder with internal heat sources. Journal of Statistics and Mathematics 3(2): 109-113.
- Bagde SD, Khobragade NW (2012) Heat conduction problem for a finite elliptical cylinder. Int Journal of Scientific & Engineering Research 3(8): 1-3.
- Khobragade NW, Khalsa L, Kulkarni A (2013) Thermal deflection of a finite length hollow cylinder due to heat generation. Int J of Engg and Innovative Technology 3(1): 372-375.
- Khobragade NW (2013) Thermoelastic analysis of a thick hollow cylinder with radiation conditions. Int J of Engg and Innovative Technology 3(4): 380-387.
- Ranjana SG, Ashwini M, Khobragade NW (2014) Interior thermo elastic solution of a hollow cylinder. IJEIT 4(1): 206-211.
- Singru SS, Chauthale S, Khobragade NW (2015) Thermal stress analysis of a thick hollow cylinder. IJEIT 5(3): 157-160.
- Singru SS, Khobragade NW (2017) Integral transform methods for inverse problem of heat conduction with known boundary of semi-infinite hollow cylinder and its stresses. IJLTEMAS 6(4): 5-9.
- Vivek F, Warbhe MS, Khobragade NW (2018) Thermal stresses of semi-infinite hollow cylinder with internal heat source. IJLTEMAS 7(2): 29-34.
- El Dhaba AR, Ghaleb AF, Abou DMS (2003) A problem of plane, uncoupled linear thermoelasticity for an infinite, elliptical cylinder by a boundary integral method. Journal of Thermal Stresses 26(2): 93-121.
- El Dhaba AR, Ghaleb AF, Abou DMS (2015) Deformation for a rectangle by a finite Fourier transform. Journal of computational and theoretical nanoscience 12(1): 31-37.
- El Dhaba AR, Abou DMS (2015) Thermal stresses induced by a variable heat source in a rectangle and variable pressure at its boundary by finite Fourier transform. Journal of thermal stresses 38: 677-700.
© 2018 NW Khobragade. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






