Mathematical Modeling of Microwave Heating in a Slab: Taylor Series Method

Microwaves are a type of electromagnetic radiation, which are waves of electrical and magnetic energy travelling through space. The spectrum of electromagnetic radiation includes both powerful X-rays and weaker radio frequency waves that are employed in broadcasting. The radio frequency band of electromagnetic radiation includes microwaves.

Microwave heating has found widespread use in the energy, construction, forestry, chemical and food industries, etc. Three features of microwaves make it possible to employ them for cooking: they are absorbed by metal and passthrough materials like glass, paper and plastic [1]. Numerous industrial processes, including those involving melting, smelting, sintering, drying, and joining, have found new uses for this technology [2].

Heating by microwave radiation is a reaction-diffusion problem with a radiative heat source term, and due to the long-term behaviour of the solutions in space, the system may develop hotspots or localised areas of excessive heating [3]. To solve this problem, several numerical techniques, including finite differences, the spectrum method, the gunshot method, etc., have emerged in recent decades. With the introduction of unique hybrid numericalanalytical systems for nonlinear differential equations, the concepts of classical analytical methods have recently undergone a renaissance.

To analyse the mathematical model to get insight into an essentially complicated physical process to forecast the occurrence of such events. The theory of response diffusion equations is exceedingly complex, and it is still very difficult to solve these equations in rectangular, cylindrical, and spherical coordinates with any practical relevance in the engineering sciences. With the development of new hybrid numerical-analytical systems for nonlinear differential equations, the concepts of classical analytical methods have recently done revival.

Hermite-approximation Pade’s approach is one such trend [4- 6]. Makinde [7] applies Hermite-approximation Pade’s method for solving the steady-state nonlinear equation in a temperature field. For a better understanding of these processes and the development of highly efficient microwave installations, simple mathematical modeling is needed. In this paper, we obtain the simple analytical expression for the temperature field by solving the nonlinear equation using the Taylor series method.

The steady-state nonlinear diffusion equation with the source term, which describes the thermal behaviour of the basic microwave heating model can be expressed as follows [8]:

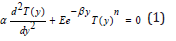
The boundary conditions are

where T is the temperature, γ is the distances measured in the normal direction, E represents the amplitude of the incident radiation, α denotes the thermal constant, β is the electric field amplitude decay rate and n is the thermal absorptivity index, a is the slab of half width and T₀ is the wall temperature. By introducing the following dimensionless variables

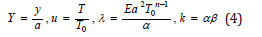
the nonlinear differential equation (1) becomes the dimensionless form as follows:

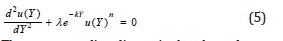
The corresponding dimensionless boundary conditions are

whereis the dimensionless temperature field, λ is the thermal absorptivity parameter, k is the electric filed decay rateand Y is the dimensionless distance.

Numerical and analytical solutions of the ordinary/partial differential equations (ODEs) by using the Taylor series method have been investigated by many authors [9-21] and references therein. The dimensionless temperature field can be obtained by solving the equation (5) using Taylors’s series method as follows:

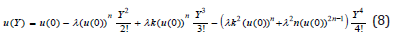
Using the boundary condition, u(1) =1 in Eq. (9) gives the numerical value of u(0) . For examples the experimental values of the parameters λ = 0.1, k = 0.1,and n = 0.1 and u(0) = 1.04865 . The analytical expression for the temperature field takes on the form

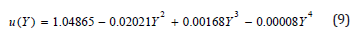
Hermite- Pade´ approximation method was applied by Makinde [7] to solve Eq. (5) with boundary conditions (6) and (7). The analytical expression for the temperature field is obtained

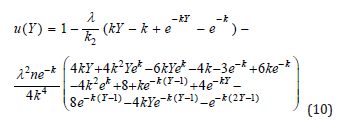
Equations (6) and (7) numerically solve the nonlinear Eq. (5) in the temperature field for the boundary condition. The Scala/Matlab (Appendix B) software’s function pdex1 was used to numerically solve problems including initial-boundary values for non-linear differential equations. The present and earlier analytical results are compared to this numerical solution in Tables (1-3). A satisfactory agreement is indicated.

Table 1:Comparison of dimensionless temperature field u(Y) with simulation results for various values of parameter λ when “k=0.1” and “n=0.1”.

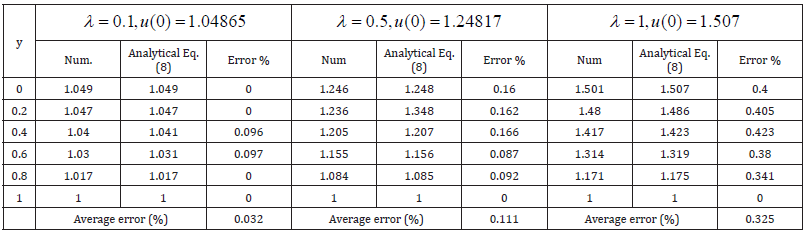
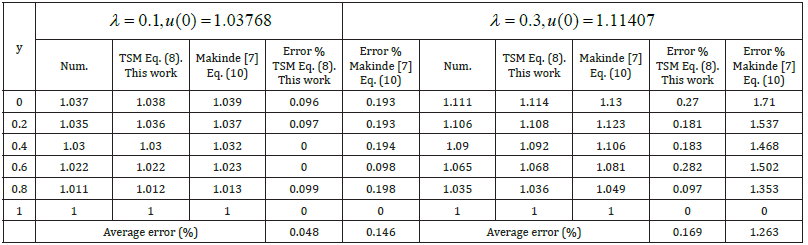
Table 2:Comparison of dimensionless temperature field u(Y) with simulation results for various values of parameterk when λ”=0.1” and “n=0.1”.

Table 3:Comparison of dimensionless temperature field u(Y) with simulation results and previous analytical results for k=1,and n=0.1.

Europe still has a long way to go in this form of justice. Legal proceedings are still mainly conducted on the basis of conventional environmental law, administrative law and human rights. Climate issues are gaining ground [32]. In Europe, a study on rights of Nature was published in 2020: “Towards a European Union Charter of the fundamental Rights of Nature” [33]. In 2021 a study followed at the request of the European Parliament: “Can Nature get it right?” [34]. In six European countries, rights of Nature in the constitution are (or have been) the subject of debate: Finland, France, Germany, Italy, Portugal, and Sweden. Initiatives are also being developed in the UK, Ireland and Denmark [35].

In the Netherlands, activists plead for rights of the Wadden Sea [35], and of the river Maas (‘Maas in the law’ initiative, which is wordplay since it is also a Dutch expression (for a gap in the law). The Rotterdam design museum the new institute has become the first Zoop in the world where nature also has a voice in the board through the board observer ‘Speaker for the Living’ (zo-operation is contraction of cooperative and ‘zoe’, life in Greek) [30]. With this, careful first steps have been taken towards better protection of the Earth, Nature, biodiversity and combating climate change. The Mar Menor example shows that biocentric approaches and sentiments can be resuscitated in Europe as well, once the disaster to Nature is sufficiently large to cause a general wake-up call [35-41].

Figure 1: Comparison of analytical expression of temperature field u(Y ) with simulation results for various value of parameter λ using eq. (8) and Makinde result using the eq. (10).

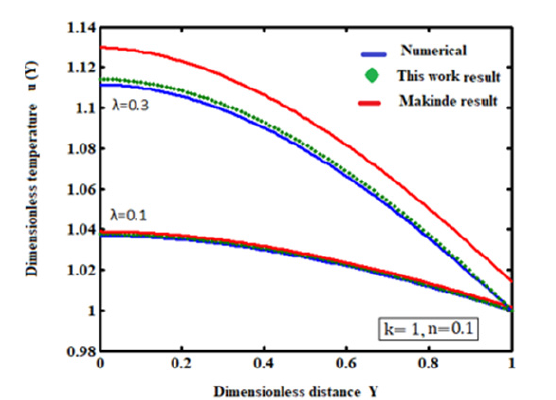
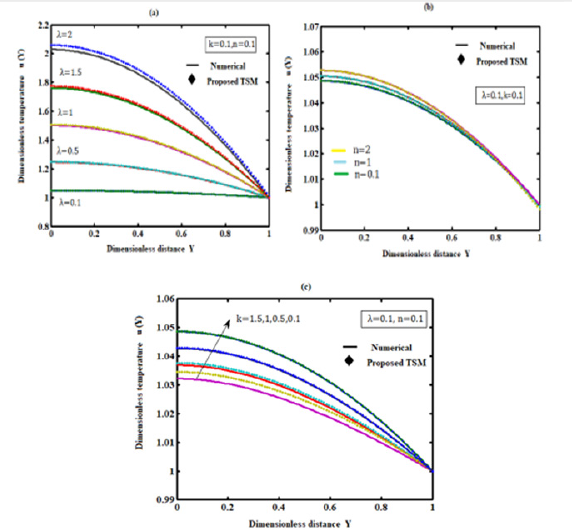
Equation (8) represents the approximate analytical expression of the temperature profile. The parameters λ, k and n which are fundamental for applications in industrial safety and explosives handling techniques, determine the thermal decomposition of the reacting combustible material. Our analytical results are compared with simulations results and previous analytical results for various values of λ in Figure 1. Figure 2(a-c) represents the effects of the thermal absorptivity, thermal absorptivity index, and Electric field decay rate parameter on a temperature profile for the various reaction mechanism. From the figure, it is observed that the temperature increases with increasing the thermal absorptivity. From the figure, it is observed that temperature decreases, and the electric field decreases.

Figure 2:Comparison of analytical expression of temperature field u(Y ) with numerical results for various value of parameters λ , k and n using eq. (8).

We studied the microwave heading model in the slab under thermal absorptivity, thermal absorptivity index, and electric filed decay rate. The steady-state nonlinear diffusion equation in microwave heating in the slab is solved using the analytical method. The simple and new closed form of analytical expression of temperature field is reported. The results illustrate that this method gives a highly accurate and good approximation of the solution to this nonlinear system.

List of symbols

Appendix A: Analytical expressions of the temperature field using Taylor series method

Using the Taylor’s series, the dimensionless temperature can be expressed as follows:

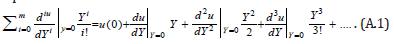
Eq. (5) in the text can be expressed in the form

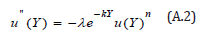
Taking the derivative of Eq. (A.2)with respect to gives

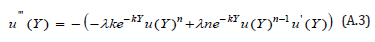
Substitute in Eq. (A.2) and Eq. (A.3) implies

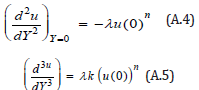
Successive differentiation of Eq. (A.3) gives

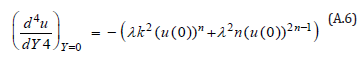
Appendix B

Matlab program: Scilab/ Matlab program for the numerical solution of the system of nonlinear Eq.(5)

function pdex4
m = 0
x = linspace(0,1)
t= linspace(0,10000)
sol = pdepe(m, @pdex4pde, @pdex4ic, @pdex4bc, x, t)
u1 = sol( :, :,1)
figure
plot(x,u1(end,:))
title(‘u1(x,t)’)
xlabel(‘Distance x’)
ylabel(‘u1(x,2)’)
%------------------------------------------------------------------ function [c, f, s] = pdex4pde(x, t, u, DuDx)
c = 1
f = DuDx
a=0.1; b=0.5
F =a*exp(-b*x)*u^(0.1)
s = F
function u0 = pdex4ic(x)
u0 = 1
function[pl, ql, pr, qr]=pdex4bc(xl, ul, xr, ur, t)
%create a boundary conditions
pl = 0
ql = 1
pr = ur-1
qr = 0.

1. Hill JM, Marchant TR (1996) Modelling microwave heating. Appl Math Modelling 20 (1): 3-15.
2. Kriegsmann GA (1992) Thermal runaway in microwave heated ceramics: A one-dimensional model. J Appl Phys 71(4): 1960-1966.
3. Coleman CJ (1990) On the microwave hotspot problem. J Aust Math Soc Ser B 33(1991): 1-8.
4. Guttamann AJ (1989) Asymptotic analysis of power - series expansions. In: Domb C, Lebowitz JK (Eds.), Phase transitions and critical phenomena, Academic Press, New York, USA, pp. 1-234.
5. Makinde OD (1999) Extending the utility of perturbation series in problems of laminar flow in a porous pipe and a diverging channel. J Austral Math Soc Ser B 41: 118-128.
6. Tourigny Y, Drazin PG (2000) The asymptotic behaviour of algebraic approximants. Proc Roy Soc London A 456(1997).
7. Makinde OD (2007) Solving microwave heating model in a slab using Hermite-Pade´ approximation technique. Applied Thermal Engineering 273(2-3): 599-603.
8. Hill JM, Pincombe AH (1991) Some similarity temperature profiles for the microwave heating of a half-space. J Aust Math Soc Ser B 33(1992): 290-320.
9. Barrio R, Rodriguez M, Abad A, Blesa F (2011) Breaking the limits: The Taylor series method. Applied Mathematics and Computation 217(20): 7940-7954.
10. Marzban HR, Razzaghi M (2006) Solution of multi-delay systems using hybrid of block-pulse functions and Taylor series. Journal of Sound and Vibration 292(3-5): 954-963.
11. Neidinger D (2004) Directions for computing truncated multi variate Taylor series. Mathematics of Computation 74 (249): 321-340.
12. Jeyabarathi P, Rajendran L, Abukhaled M, Kannan M (2022) Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalysts shapes. Reaction Kinetics, Mechanisms and Catalysis 135: 1739-1754.
13. Jeyabarathi P, Kannan M, Rajendran L (2021) Approximate analytical solutions of biofilm reactor problem in applied biotechnology. Theoretical Foundations of Chemical Engineering 55(5): 851-861.
14. Sylvia SV, Salomi RJ, Rajendran L, Abukhaled M (2020) Poisson-Boltzmann equation and electrostatic potential around macroions in colloidal plasmas: Taylor series approach. Solid State Technol 63(3).
15. He JH, Ji FY (2019) Taylor series solution for Lane-Emden equation. Journal of Mathematical Chemistry 57: 1932-1934.
16. He CH, Shen Y, Ji FY, He JH (2020) Taylor series solution for fractal Bratu-type equation arising in electrospinning process. Fractals 28(1): 1-8.
17. Salai Sivasundari SA, Usha Rani R, Lyons MEG, Rajendran L (2022) Transport and kinetics in biofiltration membranes: New analytical expressions for concentration profiles of hydrophilic and hydrophobic Vocs using taylor’s series and Akbari- Ganji methods. Int J Electrochem Sci 17: 1-17.
18. Umadevi R, Chitra Devi M, Venugopal K, Rajendran L, Lyons MEG (2022) Theoretical analysis of reaction-diffusion process in biocatalyst modified electrodes: Solutions derived via Akbari-Ganji method and Taylor’s series with Ancient Chinese algorithms. Int J Electrochem Sci 17: 1-16.
19. Mary MLC, Chitra Devi M, Meena A, Rajendran L, Abukhaled M (2021) A reliable Taylor series solution to the nonlinear reaction-diffusion model representing the steady-state behaviour of a cationic glucose-sensitive membrane. J Math Comput Sci 11(6): 8354-8381.
20. Vinolyn Sylvia S, Joy Salomi R, Rajendran L, Abukhaled M (2021) Solving nonlinear reaction-diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. Journal of Mathematical Chemistry 59: 1332-1347.
21. Usha Rani R, Rajendran L, Lyons MEG (2021) Steady-state current in product inhibition kinetics in an amperometric biosensor: Adomian decomposition and Taylor series method. Journal of Electroanalytical Chemistry 886: 115103.