- Submissions

Full Text
Novel Research in Sciences
S-curves and Entropic Conditions of System Stabilization
Korablev GА*
Doctor of Science in Chemistry, Professor of Physics Department at Izhevsk State Agricultural Academy, Russia
*Corresponding author: Korablev GА, Doctor of Science in Chemistry, Professor of Physics Department at Izhevsk State Agricultural Academy, Udmurt Republic, Izhevsk, Studencheskaya St. 11, Russia
Submission: April 19, 2021;Published: May 3, 2021
.jpg)
Volume7 Issue4May, 2021
Abstract
The graphs of S-curves characterize the dynamics of change of entropic components depending on the process main parameters. The condition of the system stationary state is the equality or constant of the correlation between its entropy and negentropy. Such regularities are found in many phenomena and conformational interactions in physical chemistry, nature, engineering and even economy. The examples of their functional contribution are given. The possibility of objective analysis of the coronavirus regional scenario is demonstrated based on the Russian data.
Keywords: S-curves; Their diversity; Entropy; Negentropy; System stabilization; Physical and chemical regularities; Coronavirus scenario
Introduction
In the last century some general regularities in the development of some biological systems depending on time (growth in the number of bacteria colonies, population of insects, weight of the developing fetus, etc.) were already found [1]. The curves reflecting this growth were similar, first of all, by the fact that three successive stages could be rather vividly emphasized on each of them: slow increase, fast burst-type growth and stabilization (sometimes decrease) of number (or another characteristic). Later it was demonstrated that various engineering systems go through similar stages during their development. The curves drawn up in coordinate system where the numerical values of one of the most important operational characteristics (for example, aircraft speed, electric generator power, etc.) were indicated along the vertical and the “age” of the engineering system or costs of its development along the horizontal, were called S-curves (by the curve appearance), or they are sometimes also called “life lines”, and as applicable to engineering systems-curves of engineering system development. As an example, the graph of the changes in steel specific strength with time is demonstrated [1], (Figure 1). “It is considered that the law of S-curves does not reflect the essence of changes in the systems, it just demonstrates their result expressed in the changes of main indexes. But in reality it, without getting into technical details, allows seeing the process regularities and future tendencies in time and drawing the corresponding conclusions. S-curve is an indicator, which describes the system state and contributes to timely making decisions on finding new trends of its development. It allows shortening the technological gap, and, in case of lacking solutions, stimulating their search” [2]. Thus, S-curves are the nomograms of changes in the process main parameters. And, therefore, they are widely applied, for example, Lorentz curve. In Lorentz curve [3] the space-time graphic dependence of the velocity parameter (θ) on the velocity itself (β) is given (Figure 2).
Figure 1: Dependence of steel specific strength on time.
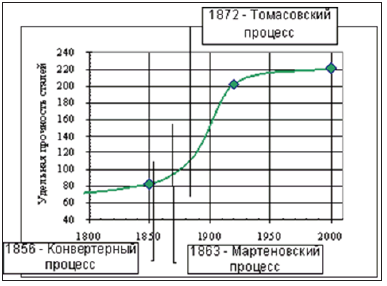
Figure 2: Connection between the velocity parameter θ and velocity itself β=thθ.
Similar examples of such nomograms in biophysics:
i. Surface-diffusive processes during nanostructure
carbonization.
ii. In kinetics of fermentative processes.
iii. Dependence of biophysical criteria on their frequency
characteristics.
iv. Fluctuations of bio-membranes conductivity depending
on their frequency.
v. Dependence of the electron transport rate on the diffusion
time of ions.
As it is known, the notion of entropy can be the criterion
of directedness of thermodynamic processes. Therefore, to
explain the unique properties of S-curves this property is used
in this investigation from the position of changes of entropy and
negentropy.
Initial Data
After analyzing the first law of thermodynamics, we have the following [4]:
a) In the systems in which the interaction proceeds along
the potential gradient (positive work), the resultant potential
energy, as well as the reduced mass are found based on the
principle of adding reciprocals of corresponding values of
subsystems. This is the corpuscular process, in which entropy
can serve as the theoretical concept.
b) In the systems in which the interactions proceed against
the potential gradient (negative work) the algebraic addition
of their masses, as well as the corresponding energies of
subsystems is performed. This is the wave process, in which
negentropy can serve as the theoretical concept.
c) The resonance stationary state of the systems is fulfilled
under the condition of equality of degrees of their corpuscular
and wave interactions. The entropy products in stationary state
are completely compensated by the negentropy flow.
Coulomb interactions and their varieties are widely applied
in classical physics and quantum mechanics to evaluate the
structural interactions in simple and complex systems. Thus in
[5] Van der Waals, orientation and charge-dipole interactions are
referred to electron-conformation interactions in biosystems. And
as a particular case-exchange-resonance transfer of energy. But
biological and many cluster systems are electroneutral in structural
basis. And non-Coulomb equilibrium-exchange energy interactions,
i.e. non-charge electrostatic processes, are mainly important for
them. The structural interactions of summed electron densities of
valence orbitals of the corresponding conformation centers take
place-processes of equilibrium flow of electron densities due to
overlapping of their wave functions. The closer are the values of
their energy characteristics, the easier is the equalizing of electron
densities.
Heisenberg & Dirac [6] proposed the exchange Hamiltonian
derived in the assumption on direct overlapping of wave functions
of interacting centers:
H=-I0S1S2
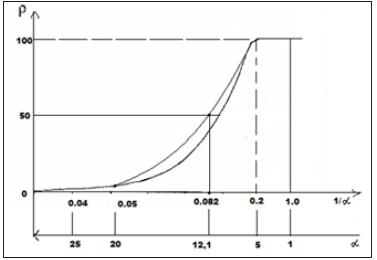
where: H -spin operator of isotropic exchange interaction for the pair of atoms; I0 -exchange constant; S1 and S2 -overlapping integrals of wave functions. Such equilibrium-exchange conformation interactions regulate the stabilization of many organic systems (clusters, polypeptide chains, etc.). Therefore, in such approach the overlapping integrals of wave functions are modeled through the value of relative difference of energy parameters of interacting centers-coefficient α [7,8]. Applying the reliable experimental data we obtain the nomogram of structural interaction degree dependence (ρ) on coefficient α, the same for a wide range of structures (Figure 3). This type of nomogram, as well as its dissymmetric variant (Figure 4) give the possibility to evaluate the degree and direction of the structural interactions of phase formation, isomorphism and solubility processes in multiple systems, including molecular ones [7,8]. The less is α, the higher is the interaction wave component degree according to (Figure 4) (negentropic curve). And in (Figure 3) the increase of α characterizes the increase in corpuscular and electrostatic properties in microsystems (entropic curve). Thus, the notion of entropy is numerically modeled via coefficient α and negentropyvia 1/α.
Figure 3:Nomogram of structural interaction degree dependence (ρ) on coefficient α.
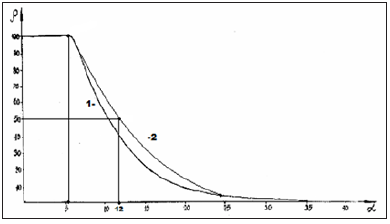
Figure 4: Nomogram of structural interaction degree dependence (ρ) on coefficient 1/α.
Conditions of Equilibrium and Correlations of Entropic Parameters
The execution of par. 3 of initial data is classified depending on the peculiarities of process dynamics. Thus, in electromagnetic wave the difference in the path of vector components is 90°. In general case, during the rotational motion of the system of two similar vectors (R) with the phase difference of 90° their resultant:
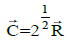 , where for the given angle tg45°=1 …(1)
, where for the given angle tg45°=1 …(1)
If such process is complemented by the movement along the spiral dynamics, the vector C becomes the tangent vector and forms the spiral rotation angle, for which:
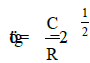 ,where geodesic angle ö equals 54.733° …(2)
,where geodesic angle ö equals 54.733° …(2)
At this angle a silk worm winds the silk thread onto a base. Thus, during purely rotational motion the condition of equilibrium of vector components of entropic characteristics is fulfilled, and during the spiral one the ratio equals 21/2. During the translational motion the conditions of either equilibrium or constant ratio of values of their components are fulfilled. At the same time, exponential dependencies are revealed in statistic processes. Such approach determines general principles of many physical regularities.
a) Characteristic of spin-orbital interaction-fine structure constant= r/ë , where r-electron classical radius, λ- its Compton wavelength.
b) π equals the ratio of circumference length (l) to its diameter (2r).
c) In [9,10] the concepts of breaking point during the extension of thread plastics by its winding pitch are used: σα -axial, σβ -circumferential stresses, which are replaced by value Nα-axial “strain” proportional to them and Nβ-circumferential “strain” by the following equation:
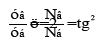 …(3)
…(3)
“This condition allows obtaining the stress-ration system of
threads with the minimum weight of the item” [10].
In harmonic oscillations of the body the potential energy ratio
conditioned by quasi-elastic force to kinetic energy equals 2 tg δ , i.e.
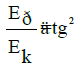 …(3a)
…(3a)
where δ-angular characteristic of oscillations.
If ä=ϕ , the system gets the entropic equilibrium state.
d) In quantum mechanics the ratio of magnetic moment of the particle to its mechanical moment is called the gyromagnetic ratio –g. Here gs=2, if the electron magnetic moment is conditioned only by the spine component and g=1, if it is formed by the orbital motion of electrons. Such g values and their ratios characterize the corresponding entropic dependencies.
e) Planck’s equation (quantum transition): h= E/v, where Е-orbital energy, constant in stationary state, the process proceeds along the field gradient (entropy), ν-electromagnetic wave frequency (negentropy), h-Planck’s constant.
f) Movement rate equation: v=S/t , where S-way during the mechanical motion with energy consumption (negentropy), t-time, always increases and is directed along the gradient (entropy). Lorentz curve (Figure 2) also indicates the availability of spacetime dependence. In these cases, the constant motion rate is the condition of stationary state, which is found both in the microcosm of atoms and molecules and in the macrocosm during the movement of planets.
g) Microstructural interactions [11]: The following equation is obtained by ρ and α values in the equilibrium state based on the initial nomogram (Figure 3):
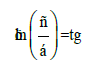 …..(4)
…..(4)
Where φ-geodesic angle, α-relative difference of energy parameters of interacting systems, ρ-structural interaction degree.
h) During the rotational motion of the charged particle in gravitation field [11]:
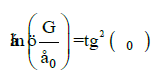 …(5)
…(5)
Where ε 0 -electric constant, G-gravitational constant, α 0 =1.00233-quantum correction to electron gyromagnetic ratio in an atom, which may, in this case, characterize the influence of particles motion precession.
i) From the thermodynamic definition of entropy it follows: T=dw/ds, where dw is thermal energy, therefore the average temperature (T) is a constant value, both in biological systems and for planets.
j) In chemical kinetics Le Chatelier principle is fulfilled:
“At the external action upon the equilibrium system, the equilibrium
will shift in the direction of the process, which resists this action”.
In such examples:
i. If the processes proceed along the gradient (entropy), the parameters are as follows: t, α, E, σα , r, å0 , Eð ;
ii. If the processes proceed against the gradient (negentropy), the parameters are as follows: S, ρ, ν, σβ , λ , μ, G, Eê , l.
S-curves in Economy
S-curves are often used in economic investigations, for instance, GDP dynamics, amount and volume of products, forecast of innovation potential, etc. Thus, the graphs of demand line (entropy analogy) and supply line (negentropy analogy) are used to evaluate the rational market price (Figure 5), [12]. From the graph it is seen that the rational market price is fixed if the demand and supply lines are in equilibrium. The diagram of GDP world dynamics is demonstrative, which almost corresponds to the negentropy graph (Figure 6), [13]. The main decrease in GDP growth has started since 2018 and it becomes very significant during the coronavirus pandemic. At the same time, GDP of China has been constantly increasing, though with delay, even in 2020. In order to avoid GDP stagnation, some negentropic economies should probably get some addition of entropic component. The Chinese experience and coronavirus busting experience already exist in the world. Thus, the countries with rather small percentage of state companies took in the situation faster and are better managing this problem.
Figure 5: Graph of demand and supply.
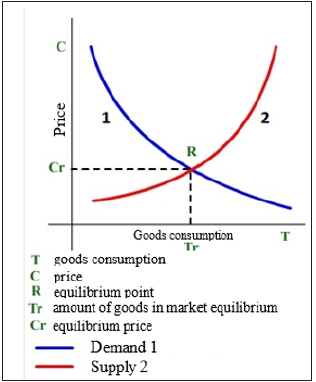
Figure 6: Graph of world GDP.

S-curves and COVID-19
Similar dynamics can be also demonstrated in virus etiology, which can be interpreted as smooth transition from atomicmolecular interactions on the microlevel to formally similar process in macrosystems. This analogy is confirmed by quantitative calculations for the coronavirus scenario. Let us consider this on the example of the Russian coronavirus scenario for the number of diseases in the given time period (ρ) in (Figure 7), [14]. Such graphs demonstrate the interaction of the process entropic components: the negentropic curve gradually transforms into the entropic one. In the initial nomograms there is a point, which splits each graph into two symmetrical parts at ρ=50%. The data detalization near this value (Figure 7) provides other values close to it. Thus, for the first wave this situation corresponds to the dates from 21.04.2020 to 25.04.2020 and provides the average value ρ=5493. This means that at ρ=100% there must be the plateau with the numerical value two times greater, i.e. 10987. Actually, within 13 days-from 03.05.2020 to 15.05.2020-the average value of ρ equalled 10661 [15]. For the second wave of the pandemic, the point of symmetric change of such graph equals approximately the half of its maximum value. If we make the correlation between the pandemic time in (Figure 7) and coefficint ɑ in the initial nomogram (Figure 3), we can evaluate the duration of the graph top plateu. Such calculation correlates with actual results [15]. The application of this technique in other regions and countries would allow analyzing and forecasting some important stages of coronavirus scenario. But in these cases it is necessary to preliminary evaluate the regional correlation coefficient.
Figure 7: Number of diseases in the given time period.

Conclusion
This approach is not conceptually new and the given examples are not singular. Thus, thousands of years ago it was found: “All phenomena of the world around us, including a human and nature, are interpreted by Chinese medicine as the interaction between two origins “Yin” and “Yang” representing opposite aspects of unified reality” [16]. From the point of these notions, physiotherapy and reflexotherapy can be considered as the technique for equalizing the potentials of two manifestations of energy origins, which, according to modern concepts, are entropy and negentropy (par. 3 of the initial data). In this pandemic situation the collective immunity acts against the virus and even cold winter contributes to forced self-isolation. In 20th century, the century of wars, epidemics and revolutions, there were huge human losses. But the coefficient of population growth was the highest during the whole humanity history. In postwar period in Russia the birth rate of boys was much higher than before the 2nd World War. At present, in the time of ecological problems, there is an important principle: all carbon dioxide produced must be absorbed. All these are the phenomena of parity correlation between entropy and negentropy.
Concluding Observations
i. The graphs of S-curves characterize the dynamics of
change of entropic components depending on the process main
parameters.
ii. The condition of the system stationary state is the
equality or constant of the correlation between its entropy and
negentropy.
iii. Such regularities are found in many phenomena and
conformational interactions in physical chemistry, nature,
engineering and even economy. The examples of their functional
contribution are given.
iv. The possibility of objective analysis of the coronavirus
regional scenario is demonstrated based on the Russian data.
References
- Kynin АТ, Lenyashin VA (2008) Evaluation of parameters of technical systems using growth curves.
- Sorokin A (2011) S-curve.
- Taylor E, Wheeler J (1992) Spacetime physics. (2nd edn), W. H. Freeman and Company, USA, pp. 1-320.
- Korablev GА (2019) On problematic issues of physical chemistry. Jmest 6(6): 10320-10324.
- Rubin AB (1987) Biophysics. Theoretical biophysics. In: Vysshaya shkola M (Ed.), pp. 1-319.
- Dirac PA (1935) Quantum Mechanics. Oxford University Press, Oxford, UK.
- Korablev GA, Petrova NG, Osipov AK, Zaikov GE (2013) Diversified demonstration of entropy. New Book Announcement. Nanotechnologies to Nanoindustry, pp. 120-130.
- Korablev GA, Zaikov GE (2012) Bio-structural energy criteria of functional states. News of HEIs, Applied chemistry and bio-engineering 1(2): 118-124.
- Pidgainy Yu M, Morozova VM, Dudko VA (1967) Mechanics of polymers. 6: 1096-1104.
- Kodolov VI (1992) Polymeric compositions and technology of producing aircraft engines from them. Izhevsk Mechanical Institute, Russia, pp. 1-200.
- Korablev GA (2020) On the mechanism of gravitation processes. Research & Development in Material Science 11(5): 1223-1226.
- Business ideas for home production.
- Gross domestic product.
- (2020) COVID-19 pandemic in Russia.
- Korablev GA (2020) Virus entropic characteristics. Journal of Multidisciplinary Engineering Science and Technology (JMEST) 7(6): 12084-12088.
- Traditional Chinese medicine.
© 2021 Korablev GА. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






