- Submissions

Full Text
Research & Development in Material Science
On the Mechanism of Gravitation Processes
Korablev GA*
Professor of Department of Physics, Izhevsk State Agricultural Academy, Russia
*Corresponding author: Korablev GA, Doctor of Science in Chemistry, Professor of Department of Physics, Izhevsk State Agricultural Academy, Russia
Submission: September 17, 2019;Published: September 24, 2019

ISSN: 2576-8840 Volume11 Issue5
Abstract
The mechanism of gravitation processes is analyzed using the condition of stationary state in corpuscularwave interactions and in the frameworks of non-relativist mechanics. The equation of functional dependence of gravitation constant upon the electric constant is obtained. It is assumed that gravitation is a wave contribution from the mass of charged particles during their movement in the field of central forces.
Keywords: Gravitation mechanism; Conditions of stationary state; Corpuscular-wave processes
Introduction
According to Newton’s classical gravitation theory, force {\displaystyleF of gravitational attraction between two material points with masses m1 and m2 divided by distance r, acts along the right line connecting them, is proportional to both masses and reversely proportional to the squared distance between them [1]. That is:
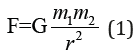
Here G-gravitational constant equaled to 6.67408(31) ·10−11 m3/(kg·s2).
Is the field is formed by point mass M located in the origin of the coordinates, the gravitational potential is determined by the following formula:
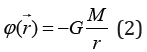
In general case, when the substance density 𝜌 is distributed randomly, 𝜑 satisfies Poisson’s equation:
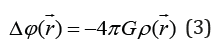
In the frameworks of non-relativist mechanics, Newton’s and Poisson’s equations allow forecasting the motion of celestial bodies with high precision. At the same time, Newtonian model is purely mathematical without any physical content [2]. It also known that the gravitational and inert mass is one and the same value defining different phenomena, whose dynamics still needs to be investigated [3,4].
Einstein’s general theory of relativity (GTR) explains the physical essence of gravitation based on the idea of change in geometrical properties and curvature of 4D space-time. In “weak” gravitational fields Einstein’s gravitational equations come down to Newton’s gravitational equation [5]. However, following the modern concepts “GTR is inadequate and gradually vanishes from the literature being replaced by the gravitation theory” [6]. New theories, explaining GTR’s new principles, emerged. The quantum theory of gravitation is the most fundamental [7], but it is considered incomplete yet. Gravitation is the only fundamental interaction, on which the generally accepted consistent theory has not been structured yet.
“The application of the principle of corpuscular-wave dualism to the gravitational field demonstrates that gravitational waves can be considered as the flow of the field quantsgravitons. From the quantum gravitation point, gravitational interaction is performed by the exchange of virtual gravitons between the interacting bodies” [2].
The idea of using the principles of corpuscular-wave dualism for explaining gravitation processes through the idea of gravitons field [1,2] looks the most rational, although it is necessary to find the main regularities of this phenomenon mechanism. Thus, the problem of physical nature of gravitation forces from the position of nonrelativist mechanics needs to be further investigated. In this work there is an attempt to analyze such problems based on the idea of the gradient of directedness of corpuscular-wave processes in the systems of different nature.
Initial data
In [8] it was obtained as follows:
1. In the systems, in which the interaction proceeds along the potential gradient (positive work) the resultant potential energy, the same as the reduced mass, are found by the principle of adding the reciprocals of the corresponding energies of subsystems. This is a corpuscular process and the entropy can become its theoretical concept.
2. In the systems, in which the interaction proceeds against the potential gradient (negative work), their masses and corresponding energies of subsystems are added algebraically. This is a wave process and the negentropy can be its theoretical concept.
3. Resonance stationary state of the systems is reached under the condition of equality of the degrees of their corpuscular and wave interactions. The entropy products in the stationary state are completely compensated by the negentropy flow.
4. These correlations are confirmed by the equations of Planck’s constant, fine structure constant and for π. As applicable to corpuscular-wave processes, the condition of dynamic stationary state is the condition of equilibrium of their degrees of structural interactions:
As applicable to corpuscular-wave processes, the condition of dynamic stationary state is the condition of equilibrium of their degrees of structural interactions:
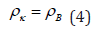
Mathematically and graphically (by nomograms) the stationary state is fulfilled by the following equation:
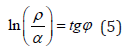
Where 𝜑= 54°44ˈ- geodesic angle, 𝛼-relative difference of energy parameters of interacting systems.
Thus, for example, for the fine structure constant this equation is as follows:
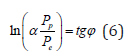
Here: Pp=WpR=938.2756МeV х 0.856fm = 803.107МeVfm
PeR=938.2756МeV>=Wer=1.43998МeVfm
𝛼-fine structure constant
Pp and Pe-energy parameters of free proton and electron
Wp and We-their energy masses
R-dimensional characteristic of proton
r-classical radius of electron.
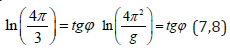
Where g-gravity acceleration.
Thus, the equality of corpuscular and wave interactions defines the resonance stationary sate of the system. This condition corresponds to the most optimal technological variants and is widely revealed in nature, as well as in fractal systems
Corpuscular-wave mechanism of gravitation
During the rotational movement of a solid (or mathematical
point) around the fixed axis, vector of complete acceleration 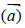 consists of two component vectors: centripetal acceleration
consists of two component vectors: centripetal acceleration 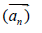 and tangential acceleration
and tangential acceleration 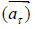 - Figure 1.
- Figure 1.
Figure 1: Kinematic characteristics of rotational movements.
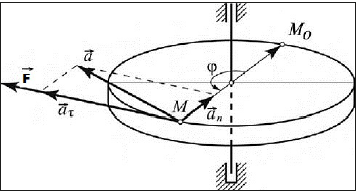
With the fixed axis of rotation, the vector of centripetal acceleration is directed to it, i.e. along the field gradient. This is a corpuscular part of the movement. The vector of tangential acceleration is directed from the system tangentially to the trajectory, i.e. against the field gradient – this is a wave part of the movement. During the uniform rotation the correlations of these equations are as follows:
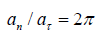
The corpuscular-wave principle of such rotational motion is confirmed by the equation (7).
During the similar movement of charged particles, the simultaneous transfer of its mass and charge occurs. Thus, in the electro diffusion equation of the transfer of charged particles the total flow intensity (J) equals the sum of the intensities of mass and charge transfer:
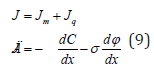
Where dC/dx – concentration gradient, d𝜑/dx – potential gradient.
In accordance with the condition of stationary state (par. 3 of the initial data), the action of the corpuscular component defines the emergence of the wave part of the process. Thus, the circular motion of charges (corpuscular process) produces the magnetic field with its poles (wave process). During the similar movement of the charged particle mass (corpuscular process) the potential field should emerge (wave process). It can be assumed that such field is gravitational, but then a definite correlation between the gravitational and electrical constants should be fulfilled. Therefore, as applicable to the kinematics of mechanical systems and preserving the formalism of equation (5) we have:
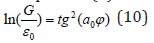
Where ε0 electrical constant, a0-quantum correction to gyromagnetic ratio of electron in the atom, which, in this case, probably characterizes the influence of precession of particles movement. This equation is fulfilled with the deviation from the initial value of 𝜑 by 0.015%. Thus, the equation (10) confirms the assumption that the wave contribution of the charged particle mass
determines the availability of the gravitational field. Therefore, the similarity of Coulomb’s and Newton’s equations is not formal, but has physical substantiation. Besides, the equality of gravitational and inert masses is determined by the equality of corpuscular and wave components. Thus: “If it is impossible to get rid of neither from gravitation nor from inertia, it is possible to consider inertia and gravitation as different sides of one and the same process” [9].
There is practically another variant of the formula (10):
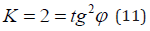
Where K-correlation of initial corpuscular and wave characteristics in this system. This equation is probably for those cases when the process initial characteristics have already taken logarithmic dependencies into account directly or indirectly. The notion of breaking stress when expanding the thread plastics by the pitch of its winding is used in [10,11]: σα - axial, σβ - circumferential stress, which are replaced by the value proportional to them Nα - axial “strain” and Nβ - circumferential “strain”. At the same time, the following equation is fulfilled:
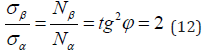
“This equation allows obtaining equally strained system of threads with the product minimal mass” [10,11].
In quantum mechanics the ratio of particle magnetic moment to its mechanical moment is called the magnetomechanical (gyromagnetic) ratio-g. At the same time, gs2, if the electron magnetic moment is conditioned only by the spin component and g=1, if it is formed by the orbital movement of electrons. Their ratio gs/g2 and tg2φ=2 characterize the corresponding corpuscularwave dependencies. More accurately with the quantum correction gs/g2.00233.
The gravitation force does not depend on the chemical composition of the bodies or particles. Each body consists of the aggregation of particles, in general case, different by nature and size. During the formation of gravitational field by microsystems, the process of proton-electron interactions under the action of central forces is considered common for all structures. In inorganic nature each system of particles in this body can be considered as closed. The graviton in it initially has the interaction direction against the field gradient. In such cases (according to par. 2 of the initial data) there is the direct algebraic addition of their intensities independently of the chemical composition of the particles forming the body mass. At the same time, the resultant intensity of gravitons is directly proportional to the body mass.
But in the wildlife each system is open, therefore, the processes of its interaction with the environment go on, but with the preservation of specific peculiarities of each particle by the gravitons. In each living organism the complex bioelectrical processes are fulfilled. For example, in DNA molecule, when winding or unwinding its structural spiral, the direction of such interactions should proceed by the geodesic angle. The silkworm works by the same angle when winding the silk thread onto the base.
In the dynamics of DNA conformation, the proton-electron interactions between the subsystems of this molecule are very important. The emerging gravitons possess the energetic and genetic information from each DNA molecule. Due to the specifics and weak intensity of such field it is not registered by ordinary devices, but can be registered by affinitive systems, as well as such systems, which can be reconstructed into the resonance from the initial. Apparently, here lies the main reason of the known effects of the so-called telepathy. But this is the biogravitation process. In inorganic nature, in some cases, for example, in cosmology, the interaction by the principle of open systems can be slightly revealed together with ordinary interactions. Probably, “space curvature” known by GTR is somehow connected with the availability of such interaction.
Conclusion
I. The mechanism of gravitation processes was analyzed using the condition of stationary state in corpuscular-wave interactions and in the frameworks of non-relativist mechanics.
II. The equation of functional dependence of the gravitational constant on the electrical constant was obtained.
It is assumed that gravitation is the wave contribution from the mass of charged particles during their movement in the field of central forces.
References
- Ivanenko DD, Sardanashvili GA (2004) Gravitation М. Editorial URSS, ISBN 5-354-00538-8.
- https://ru.wikipedia.org/w/index.php?title=Классическая_теория_тяготения_Ньютона&oldid=101565038 (Newton’s classical gravitation theory).
- ((92) Physic encyclopedic dictionary. Big Russian Encyclopedia 3: 672.
- Kittel Ch, Knight W, Ruderman M (1971) Course of physics, mechanics, science. 1: 479.
- (1988) Physic encyclopedia. Soviet Encyclopedia 1: 704.
- (1966) Physic encyclopedic dictionary. Soviet Encyclopedia 5: 576.
- Oriti D (2009) Approaches to quantum gravity. Toward a New Understanding of Space, Time and Matter. Cambridge University Press, Cambridge, USA.
- Korablev GA (2019) On problematic issues of physical chemistry. JMEST 6: 10320-10324.
- Ugarov A (1977) Special relativity theory. Science, p. 385.
- Pidgainy YM, Morozova VM, Dudko VA (1967) Mechanics of polymers. 6: 1096-1104.
- Kodolov VI (1992) Polymeric compositions and technology of producing engines for aircrafts from them. Izhevsk Mechanical Institute, Russia, p. 200.
© 2019 Korablev GA. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






