- Submissions

Full Text
Novel Research in Sciences
Entropy Criteria for Corpuscular Wave Interactions
Korablev GА*, Korablev RG and Petrova NG
Department of Physics of Izhevsk State Agricultural Academy, Russia
*Corresponding author:Korablev GА, Department of Physics of Izhevsk State Agricultural Academy, Russia
Submission: May 14, 2018; Published: July 11, 2018
.jpg)
ISSN : 2688-836XVolume1 Issue2
Abstract
The concept of entropy for space-energy interactions is used similarly to the ideas of thermodynamics of statistic entropy. This concept emerged based on the second law of thermodynamics and ideas on reduced amount of heat. Such ideas are general statements independent of microscopic models. Therefore, their application and consideration can have a large number of results, which are also most fruitfully used in statistic thermodynamics. In this investigation the attempt is made to apply such regularities to assess the degree of spatial-energy interactions using their graphical dependence in other fields as well. The nomogram to assess the entropy of various processes is obtained. The diversity of entropy manifestations is discussed, including the entropy in biophysical processes and technical systems.
The resonance stationary state of structural processes is fulfilled under the condition of equality of the degrees of corpuscular and wave interactions. This condition is also fulfilled in macroworld: the work of silkworm, production of spacecrafts, linen running-in on the base and many other examples. It is also assumed that the technology of building ancient pyramids was based on the same principles. This condition is also fulfilled in microworld, which is confirmed by the equations of Plnack’s constantconstant of fine structure and π-number. These principles can be practically applied for searching optimal technological solutions.
Keywords:Spatial-energy parameter; Wave functions; Structural interactions; Entropic nomograms; Biophysical processes; Economic and technological systems; Laws of thermodynamics; Reversible and irreversible processes
Introduction
In statistic thermodynamics the entropy (S) of the closed and equilibrious system equals the logarithm of the probability of its definite macrostate:
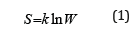
where W-number of available states of the system or degree of the degradation of microstates; k-Boltzmann’s constant.
or
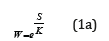
These correlations are general assertions of macroscopic character, do not contain any references to the structure elements of the systems considered and they are completely independent of microscopic models.
Therefore the application and consideration of these laws can result in a large number of consequences. The thermodynamic probability W is the main characteristic of the process. In actual processes in the isolated system the entropy growth is inevitable-disorder and chaos increase in the system, the quality of internal energy goes down. Thermodynamic probability equals the number of microstates corresponding to the given macrostate. Since the system degradation degree is not connected with the physical features of the systems, the entropy statistic concept can also have other applications and demonstrations (apart from statistic thermodynamics).
“It is clear that out of the two systems completely different by their physical content, the entropy can be the same if their number of possible microstates corresponding to one macroparameter (whatever parameter it is) coincides. Therefore the idea of entropy can be used in various fields. The increasing self-organization of human society leads to the increase in entropy and disorder in the environment that is demonstrated, in particular, by a large number of disposal sites all over the earth” [1]. In this investigation the attempt is made to apply such concepts to assess the degree of spatial-energy interactions using their graphical dependence in other fields as well.
On two principles of adding energy characteristics of interactions
The analysis of kinetics of various physical and chemical processes shows that in many cases the reciprocals of velocities, kinetic or energy characteristics of the corresponding interactions are added. On the basis of the first law of thermodynamics, an analysis was made of the nature of the change in the value of potential energy by its sign for various potential fields [2]. It was obtained that the values of - ΔU and consequently -δ A (negative work) take place during the interactions against the potential gradient. The solution of two-particle problem of the interaction of two material points with masses m1 and m2 obtained under the condition of no external forces available corresponds to the interactions taking place by the gradient, the positive work is performed by the system (similar to attraction process in the gravitation field). The solution of this equation via the reduced mass (μ) is the Lagrange equation for the relative motion of the isolated system of two interacting material points with masses m1 and m2, which in coordinate х is as follows:
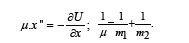
Here U-mutual potential energy of material points; μ-reduced mass.
At the same time, х″ = a (feature of the system acceleration). For elementary portions of the interactions Δх can be taken as follows:
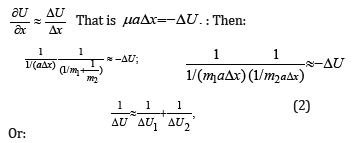
Or:
where ΔU1 and ΔU2-potential energies of material points on the elementary portion of interactions, ΔU-resulting (mutual) potential energy of these interactions.
Thus:
1. In the systems in which the interactions proceed along the potential gradient (positive performance) the Lagrangian is performed and the resulting potential energy is found based on the principle of adding reciprocals of the corresponding energies of subsystems [2]. Similarly, the reduced mass for the relative motion of two-particle system is calculated.
2. In the systems in which the interactions proceed against the potential gradient (negative performance) the algebraic addition of their masses as well as the corresponding energies of subsystems is performed (by the analogy with Hamiltonian).
Spatial-energy parameter(Р-parameter)
From the equation (10) it is seen that the resulting energy characteristic of the system of two material points interaction is found based on the principle of adding reciprocals of initial energies of interacting subsystems.
“Electron with the mass m moving near the proton with the
mass М is equivalent to the particle with the mass: 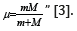
Therefore when modifying the equation (2), we can assume that the energy of atom valence orbitals (responsible for interatomic interactions) can be calculated [2] by the principle of adding reciprocals of some initial energy components based on the following equations:
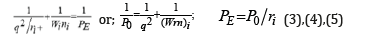
Here: Wi-electron orbital energy [4]; ri-orbital radius of i–orbital [5]; q=Z*/n* [6,7], ni- number of electrons of the given orbital, Z* and n*-nucleus effective charge and effective main quantum number, r-bond dimensional characteristics. Р0 was called a spatialenergy parameter (SEP), and РE-effective Р–parameter (effective SEP). The maximum degree of structural interaction evaluated via the coefficient a is determined by the condition of minimum value of α, which represents the relative difference of effective energies of external orbitals of interacting subsystems:
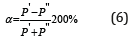
Applying reliable experimental data, the dependence nomogram of the degree of structural interactions (ρ) on the coefficient α, the same for a wide class of structures, was obtained (Figure 1). This approach allowed assessing the degree and direction of structural interactions of phase-formation, isomorphism and solubility processes in multiple systems, including the molecular ones. This type of nomogram and its ambidextrous variant (Figure 2) are widely applied to characterize many processes and phenomena in nature, engineering and even in economy. So the Lawrence curve of the space-time dependence corresponds to the nomogram in Figure 2. Therefore, such S-curves are called “Curves of life”. Some examples of such nomograms in biophysics [8]:
a. Surface-diffusive processes during the carbonization of nanostructures.
b. In kinetics of fermentative processes.
c. Dependence of biophysical criteria on their frequency characteristics.
d. Fluctuations of conductivity of bio membranes depending on their frequency.
e. Dependence of electron transport velocity on the time of ion diffusion.
Nomogram No 1 can be also displayed [2] in the form of logarithmic dependence:
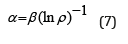
Figure 1:Nomogram of structural interaction degree dependence (ρ) on coefficient α.
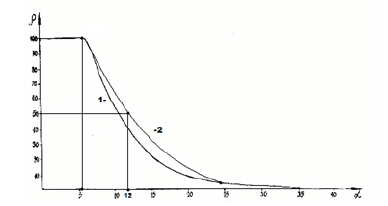
Figure 2:Nomogram of structural interaction degree dependence (ρ) on coefficient 1/α.
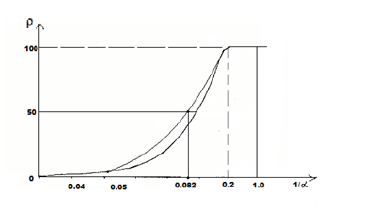
where coefficient β-constant value for this class of structures. β can structurally change mainly within ± 5% from the average value. Thus coefficient α is reversely proportional to the logarithm of the degree of structural interactions and therefore can be characterized as the entropy of spatial-energy interactions of atomic-molecular structures. Actually the more is ρ, the more probable is the formation of stable ordered structures (e.g. the formation of solid solutions), i.e. the less is the process entropy. But also the less is coefficient α. The equation (7) does not have the complete analogy with entropic Boltzmann’s equation (1) as in this case not absolute but only relative values of the corresponding characteristics of the interacting structures are compared, which can be expressed in percent. And this refers not only to coefficient α but also to the comparative evaluation of structural interaction degree (ρ), for example-the percent of atom content of the given element in the solid solution relatively to the total number of atoms. Therefore, in equation (7) the proportionality coefficient equals 1.
Conclusion: The relative difference of spatial-energy parameters of the interacting structures can be a quantitative characteristic of the interaction entropy: α≡S.
Corpuscular-wave mechanism
The formalism of equations (3,4) is not principally new. The following equation was obtained by Compton effect in 1924 already:

Here: hν›-dissipated photon energy, hν-falling photon energy, mc2-electron own energy, ϴ-dissipation angle. At the same time, the energy of photons decreases by the value additionally obtained by the electron. The act of quantum action takes place in this way, the result of which is the energy redistribution between corpuscular and wave parameters of interacting systems, which, apparently, is contained by the particle itself. In this process, the same way as during photo effect, the interaction proceeds by the potential gradient and the work is positive.
In atom during quantum transitions the interaction of similarly charged particles (electrons) is realized by irradiation, i.e. by the wave process. At the same time, for oppositely charged particles (electrons and atom nucleus) the process proceeds along the potential gradient, i.e. the corpuscular mechanism is realized. Each particle can have three main types of motion: translational, rotational and oscillatory. Quantum mechanics does not consider the issue of electron trajectory because it is possible to speak only about the possibility of its position in the given point in space.
But the electron moves and if the translational movement flows along the potential gradient then it can correspond to the corpuscular process, and the rotational motion-to the wave one (i.e. against the field gradient). Electric current is the motion of electrons along the potential gradient. If we assume that the magnetic field created by it is a wave process, there should be the correlation between electric and magnetic constants. The difference between phases of electric and magnetic oscillations is π/2.
Entering coefficient (2/π )2 we have the equation for Planck’s constant with the accuracy close to the one of the initial data.
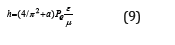
Here а = 0.0023293-experimental quantum correction to spine gs-factor of the electron, ɛ-electric constant, μ-magnetic constant, h-Planck’s constant. For a free electron Pе=Wr, where W = 0.510034 МeV= 0.81872˟10-13J. The value of classical electron radius r = 2.81794˟10-15m was used as a dimensional characteristic and, therefore, Ре = 2.30712˟10-28 Jm.
The proportionality coefficient in equation (9) has the velocity dimensionality (m/sec) for the correlation (Ф/Гн), i.e. in such a way the velocity of redistributions of energy in the system “particlewave” is characterized. Summing up the formalism of equations (2,3,4,8) on all the other interactions proceeding along the potential gradient, it can be concluded that in these cases corpuscular interactions proceed, but the wave dualism corresponds to the interactions against the potential gradient.
Rotation angles
Let us consider some macroprocesses important in this case. The silk worm winds the natural (organic) silk thread only at a definite rotation angle. In cosmonautics the cellulose-viscose thread is wound around the metal cylinder of the spaceship following the special technology, and, what is important, at the same winding angle as the silkworm. The spaceship becomes most durable, more technologically high-quality and lighter [9,10]. We can also speak of other examples of such phenomenon.
This angle (mainly as applicable to organic systems) was called the geodesic angle: φ = 54.730 = 54044’.
In [9,10,11] the concepts of breaking point during the extension of thread plastics by its winding pitch are used: σα-axial, σβ-circumferential stresses, which are replaced by value Nα-axial “strain” proportional to them and Nβ-circumferential “strain”. At the same time, the following equation is executed:
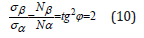
“This condition allows obtaining the stress-ration system of threads with the minimum weight of the item” [9,10]. Thus, the rotation angle numerically determines the correlation of triangle two legs, whose values characterize energy dependencies in the system with quantum and wave processes via axial and circumferential stresses. All this is widely revealed in many macroand microprocesses. Here are some examples.
1) Characteristic of spin-orbital interaction-fine structure constant = r/λ, where r-electron classical radius, λ-its Compton wavelength.
2) Formally but similarly: interaction force of two long conductors with current is proportional to the ratio l/2πr, where l-length of conductors, r-distances between them.
3) π equals the ratio of circumference length to its diameter.
4) In quantum mechanics the ratio of magnetic moment of the particle to its mechanical moment is called the gyromagnetic ratio-g. Here gs=2, if the electron magnetic moment is conditioned only by the spine component and g = 1, if it is formed by the orbital motion of electrons. Their ratio gs/g = 2 and also tg2φ=2 characterize the corresponding corpuscular-wave dependencies.
5) Babylonian Table written thousands of years ago is based on the ratio of rectangular triangle legs. Apparently this trigonometry was used for unique constructional works, whose mechanism is still unknown.
In these examples, the same as in many others, this approach allows assessing structural interactions based on their corpuscular and wave dependencies in each action, e.g., in the equation of the dependence of rotational and orbital motion of planets [12]. Using the logarithm in the ratio ρ/α to obtain the linear dependence with the rotation angle we have:
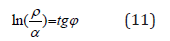
In homogeneous systems with the proximity of the values of their P-parameters (wave process) if α→0, then tgφ→∞, and φ=90°. With the corpuscular interaction mechanism if α→∞, then tgα→0, and φ=0 In general case, in the system “particle-wave” the rotation angle φ changes from 0° (at ρ=0%) up to 90° (at ρ=100%). It can be as assumed that an equally strained system is obtained under the condition of approximate equilibrium of corpuscular and wave parameters. I.e. ρ=50% at the geodesic angle. The calculation of coefficient α by the equation (11) gives 12.16%, which approximately corresponds to the coordinates obtained in the nomogram in Figure 1.
Entropy in corpuscular-wave processes
In the second law of thermodynamics only those processes are possible in the isolated system, which flow with entropy increase (ds):
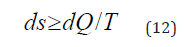
where dQ-change in the heat energy, T-thermodynamic temperature.
In thermodynamics reversible and irreversible processes are distinguished. Thus, in irreversible expansion the gas transits from less probable to more probable state, i.e. this process flows along the probability gradient. Similarly, the transit of heat from a hotter body to a colder one is irreversible, which also flows along the temperature gradient. As it was already demonstrated, corpuscular interactions also flow along the field gradient. Therefore, it is presumed that the entropy can be a theoretical concept of corpuscular processes. In the open system there is an interaction with the external environment and general change of the entropy (ds) is expressed by the equation:
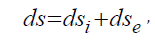
where dsi -changes of the entropy as a result of the processes inside the system, dse change of the entropy conditioned by the interaction with the external environment. Then within the time dt:
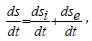
where ds/dt-total velocity of the entropy change in the closed system, dsi/dt -entropy products, dse/dt - entropy flow (negative entropy). For the dynamic stationary state the total velocity of entropy change must equal zero: ds/dt=0
And then 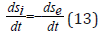
Thus, the entropy products in the stationary state are completely compensated by the negative entropy flow. The processes flowing in an open system are reversible. For example, all mechanical processes without friction belong to them. But there is friction in actual processes, as well as the conversion of mechanical work into heat, and this is already an irreversible process [13]. In the thermal machine there is heat conversion from a colder body to a hotter one. In this case and in all reversible processes the work is performed against the field gradient. And the entropy corresponding to these processes is called negative entropy. As it was demonstrated, the system work against the field gradient corresponds to the wave processes, e.g., in electric field generator.
Such analogy in directed entropic and corpuscular-wave processes allows assuming that the entropy is a theoretical concept of corpuscular interactions, and negative entropy-a concept of wave interactions. Besides, this analogy gives the possibility to use the entropic equation of the stationary state of open systems for the corresponding corpuscular-wave processes. At the same time, the following correlation is fulfilled in the heat machine: “At the circular process the increase in the system entropy due to the incoming heat is completely compensated by the decrease in entropy due to the heat output, and the total entropy value equals zero” [14]:
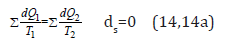
As applicable to corpuscular-wave processes, the condition of dynamic stationary state is the condition of equilibrium of their degrees of structural interactions:

This condition is graphically fulfilled when nomogram No 1 (entropy) is overlapping nomogram No 2 (negative entropy), which gives the following value:
ρ=50%.
Such equality of corpuscular and wave interactions determines the resonance stationary state of the system and it corresponds to the most optimal technological variants.
The stationary state is mathematically fulfilled by the equation (11). Thus, e.g., for the constant fine structure this equation is as follows:
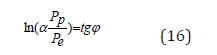
Here: Pp =Wp R=938.2756 МeV х 0.856 fm = 803.107 МeVfm
Pe=We r=1.43998 МeVfm
α-fine structure constant
Pp and Pe-energy parameters of free proton and electron
Wp and We-their energy masses
R-dimensional characteristic of proton [15]
r-classical radius of electron
φ-geodesic angle.
The equation (16) is fulfilled within the accuracy limit of the initial data.
Similarly for the equation for π:
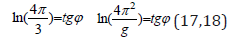
Here g–acceleration of free fall, and coefficient 4π2/g is used in the equation of dependence of rotational and orbital motion of planets [11].
The equations (17,18) are fulfilled with the accuracy of up to 1%. But such possible deviations are graphically shown in nomograms No 1 and No 2.
Conclusion
The resonance stationary state of structural processes takes place under the condition of equality of the degrees of corpuscular and wave interactions-equation (15). This condition is fulfilled in the macroworld: work of a silkworm, production of spaceships, linen winding on the base and many other examples. It is assumed that construction technology of ancient pyramids was also based on the same principles. This condition is also fulfilled in the microworld, which is confirmed by the equations of Planck’s constant, fine structure constant and for π. The conclusions obtained can be practically used to seek for optimal technological solutions.
Acknowledgement
The author thanks the co-authors of scientific papers in multifaceted manifestation of entropy-Prof. G.E. Zaikov, Prof. VI. Kodolov, Prof. Yu G. Vasiliev, Prof. P.L. Maximov, Prof. AK. Osipov and Assoc. Prof. PB. Akmarov.
References
- Gribov LА, Prokofyeva NI (1992) Basics of physics. OJSC Vysshaya Shkola Publishers, Moscow, Russia, p. 430.
- Korablev GA (2018) Spatial-energy interactions. Monograph. Stary Oskol p. 132.
- Eyring G, Walter J, Kimball G (1948) Quantum chemistry. p. 528.
- Fischer CF (1972) Atomic Data. 4: 301-399.
- Waber JT, Cromer DT (1965) J Chem Phys 42(12): 4116-4123.
- Clementi E, Raimondi DL (1967) J Chem Phys 38(11): 2686-2689.
- Clementi E, Raimondi DL (1963) J Chem Phys 47(4): 1300-1307.
- Rubin АB (1987) Biophysics. Book 1. Theoretical biophysics. Vysshaya Shkola Publishers, Moscow, Russia, p. 319.
- Pidgainy YM, Morozova VM, Dudko VA (1967) Mechanics of polymers 6: 1096-1104.
- Ayusheev TY (2005) Geometrical issues of adaptive technology for producing structures with winding from fiber composite materials. Ulan-Ude: BNC SO RAS Publishers, Moscow, Russia p. 212.
- Kodolov VI (1992) Polymeric compositions and technology of producing engines for aircrafts from them. Izhevsk Mechanical Institute, Izhevsk, Russia, p. 200.
- Korablev GA (2017) On dynamics of rotational motions in macro- and microsystems. European Chemical Bulletin 6(2): 79-82.
- Chulanovskaya MV (1972) Course of physics for biologists, part 1. Leningrad University, Russia, p. 248.
- Gevorkyan RG, Shepel VV (1972) Course of general physics. Vysshaya Shkola Publishers, Moscow, Russia, p. 600.
- Murodyan RM (1977) Physical and astrophysical constants and their dimensional and dimensionless combinations. Fiz Elem Chast Atom Yadra 8(1977) 175-192.
© 2019 Korablev GА. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






