Influence of the Structure of a Multiphase Polycrystal on Local Fluctuations of Invariants of Stress/Strain Tensors, Energy of Shape/Volume Change

Introduction

In most modern works, a material deformed under load is considered as a hierarchically organized system of elements of different scales. This system evolves during loading and adapts to the applied impacts, and the elements of its internal structure the microstructure are capable of self-organization. Given the impossibility of considering in detail the interactions of material particles of different phases in a representative volume, it is advisable to construct equations of connection between macro and microstates that satisfy the laws of thermodynamics and the condition of the uniqueness of the solution of the problem of representing real material in the model [1,2]. The advantage of phenomenological models built on fundamental principles is their generality, regardless of some details about the evolution of the structure, deformation mechanisms, etc. To describe the behavior of multiphase polycrystals in the reversible region of deformation, two-level models are used [1]. It is assumed that stresses t_ij and strains d_ij at a given point of a representative volume depend only on the orientation of the crystallographic axes of the grain and do not depend on the position of a given point inside it. This means that the deformations within the grain are considered homogeneous, which excludes the bending and curvature of grains from being considered. In addition, regardless of the position of a given grain, the stress and strain in a subset of grains with a given orientation of the crystallographic axes are also assumed to be the same. With this formalization of a continuous medium, the real environment of the crystallite is replaced by a homogeneous medium with effective properties, and the shape of the crystallite is assumed to be ellipsoidal.

If an external uniform field is applied to such a medium with an inclusion, i.e., a field that in the absence of the inclusion would be uniform throughout the entire region of the representative volume, then inside the inclusion, as shown in [3], the field will also be uniform. As part of this formalization of the environment, Kroner the following relationship was established between local t_ij,d_ij and macroscopic t_ij, d_ij stresses and strains.

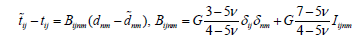
Where G is the macroscopic shear modulus ν and is Poisson’s ratio.

Krener’s approach was further developed in [4-6]. The disadvantages of models based on linear relationships between stress and strain fluctuations include inconsistency with the first law of thermodynamics. The work [7] shows that

for any variants of the tensor values B_ijnm , with the exception of the limiting values:B_ijnm=0(uniform stress state), B_ijnm = ∞ (uniform deformed state). Note that within the framework of linear relationships, only deviatoric quantities change within each phase; volumetric stresses and strains change only during the transition from one phase to another.

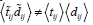
In [7-9], an approach was developed in which the relationship between stresses and strains is established without limiting the shape of the structural elements. The developed model is based both on the classical principles of mechanics and thermodynamics, and on three additional principles: averaged connections [7], orthogonality of fluctuations of stress and strain tensors [8], extremum of discrepancy between macroscopic measures and suitable average values of microscopic analogues [9]. Based on them, it is possible to describe a wide range of thermorheological effects not covered by other models. In particular, the dependence of volumetric stresses/strains of sub elements on the orientation of the crystal lattice, a decrease in the plasticity of the material with decreasing temperature, grain size, increasing strain rate, the effect of cyclic loading of maximum normal stresses, in sub elements, under monotonic macroscopic influence, etc. Within the framework of a model based on nonlinear equations connecting local and macroscopic parameters, the behavior of only singlephase polycrystalline materials was studied. In this work, we will consider the pattern of changes in extreme values of stress invariants, strains, and energies of shape/volume change in a system of sub elements of a multiphase material.

Principles of transition from micro stresses and strains to macro stresses and strains

To describe reversible deformation processes, we consider a two-level constitutive model. It is assumed that the elementary volume of the material consists of an infinite number of interconnected sub elements having different thermorheological properties. Stresses and strains satisfy the principles of R Hill [10]

where t_ij , d_ij stress and strain tensors at each point of the region, ΔV₀ respectively, t_ij , d_ij macroscopic stress and strain tensors, . volume averaging sign ΔV₀ . Each sub element is identified with a set of material particles inside a representative volume that have the same characteristics. Particles of the same sub element can have different positions in the space of the conglomerate. The number of particles in each sub element determines their weight and does not change during deformation. It is assumed that the interaction between particles of a given sub element with particles of other sub elements leads to a state similar in nature to the interaction of a sub element with a homogeneous matrix of material with effective characteristics. Because of this, a principle has been formulated: the interaction between sub elements in a representative volume is formed under the influence of only averaged connections.

The problem of the equality of the sum of the deformation energies of sub elements and the macroscopic deformation energy is solved based on the principle of orthogonality of vibrations of the stress and deformation tensors.

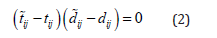
the stress and strain tensors into spherical and deviatoric components in (2)

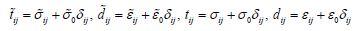
we obtain the following scalar equation for the connection between macro and microstates

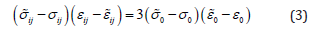
For fluctuations of stress and strain deviators, we accept the simplest expression

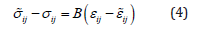
Where B is an internal parameter reflecting the inhomogeneity of the distribution of stresses and strains in a representative volume.

In accordance with [8,9], microscopic variables that have a certain physical meaning are divided into two categories: variable averaged values of which depend only on the data on the surface of the representative volume and variable averaged values of which depend not only on the data on the surface of the representative volume but also on the structural features of the material. It is shown natural macroscopic measures of the energy of change in volume and shape do not coincide with the corresponding averaged micro measures. It is natural to assume that variables containing information about the characteristics of the microstructure of a material have certain fundamental properties. In [9], the principle of extremum discrepancy between macroscopic measures and suitable average values of microscopic analogues is proposed. In particular

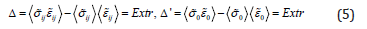
Expressions (1), (3), (5) represent a closed system of equations for the relationship between macro and microstates. They do not contain references to the properties of the material; therefore, they are valid both for describing reversible and irreversible deformation processes. On their basis, it is possible to construct constitutive equations at the macroscopic level if the constitutive equations at the microscopic level are known. Note that in multi element models, averaging is performed not over volume, but over a set of realizations, i.e. the use of the ergodic hypothesis is considered legitimate. In the elastic region, the values ij t , ij d are determined by averaging over the orientation factor of the crystal lattice.

Definition elasticity constants and heterogeneity of a polycrystal with a cubic lattice

Let us represent the relationship between stresses and strains in crystals with cubic symmetry in the form.

where C=C₄₄ is the crystal shear constant (relates shear stress to shear strains), A is the anisotropy factor (A = 2C₄₄/C₁₁−C₁₂ )) , K is the volumetric modulus of elasticity of the crystal, x’_i crystallographic coordinate system, x_i is the global coordinate system. Note that the use of constants that have a clear physical meaning simplifies the writing of the equations used. We denote the elasticity constants of crystals, stress and strain in phase with weight c_k through

. Considering these notations in (6), (5), after simple transformations we obtain the following relations between local and macroscopic deformations.

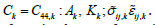
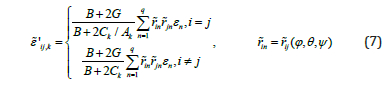
where ϕ,θ ,ψ are the Euler angles (they specify the orientation of the orthogonal axes of crystallites relative to the main macroscopic coordinate system).

Writing (7) in the global coordinate system and integrating over the crystal lattice orientation factor, we obtain.

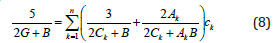
When deriving (8), we considered the formulas.

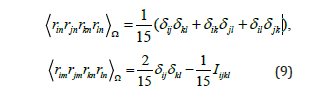
Note that in these formulas summation over n and m is not performed.

Considering (7) in (5) and integrating the resulting expression considering (9) we find

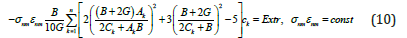
System of equations (7), (10) in the case of single-phase polycrystalline materials has a simple analytical solution [9].

Here GV the shear modulus obtained in [11] within the framework of approximation d_ij = d_ij ; shear modulus obtained in [12] within the framework of the approximation t_ij =t_ij . It is important to note that for a single-phase polycrystal with a cubic lattice, the discrepancy between the measures

, in the reversible region of deformation depends only on the anisotropy factor [9].

For multiphase polycrystals, only a numerical solution is possible. Let us consider the patterns of changes in the macroscopic shear modulus G and the inhomogeneity parameter B using the example of three two-phase materials: Al-Cr, Al-Ni, Al-Cu. Crystals of the materials under study have the following elastic characteristics [13]: Al(A1=1.215, C₁=2.85.h, K1=3.69.h), Cr(A2=0.71, C₂=10.1.h, K₁=16.13.h), Ni(A2=2.54, C₂=12.5.h, K₂=18.h), Cu(A2=3.21, C₂=7.54.h, K₂=13.7.h), h=104 MPa. The volumetric content of the harder phase c₂ is denoted by c₂=c, In the phase Al-c₁=1-c. The results of numerical studies for the shear modulus are presented in Figure 1. The curve marked in red corresponds to the alloy -Al-Fe, lilac -Al-W, brown -Al-Cu. According to Figure 1 macroscopic shear modulus G=G(c) increases monotonically with c growth. Numerical results for parameter B are presented in Figure 2. Unlike the shear modulus G=G(c) expressions B=B(c) have a more complex form. For all materials under study, the function B=B(c) is non-monotonic with respect to c. The following pattern is observed: at small values c of the B parameter increases to a certain maximum value, and then both a continuous drop and a new growth are possible.

Figure 1:Dependence of the macroscopic shear modulus G on the volumetric content of the solid phase c.

Figure 2:Dependence of the heterogeneity parameter B on the volumetric content of the solid phase c.

It is of interest to compare the numerical solution of system (7), (10) with the result of calculation using formula (11) generalized to the case of two-phase polycrystals.

Where GV(c), GV(c) shear modulus found from (10) for two limiting cases: a homogeneous stress state (B=0) and a homogeneous deformed state B = ∞ . The calculation results for various alloy options showed that the relative deviation

. Consequently, as a first approximation, we can assume that the shear modulus G ≈ G_M is equal to the geometric mean value of the moduli obtained in two limiting cases (B=0, B = ∞ ). Based on the approximation M G ≈ G and formula (10), it is possible to obtain an analytical solution for the parameter. After a series of transformations, we establish the following cubic equation.

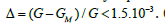
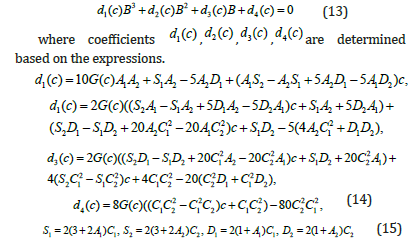
Analysis (13), (15) considering the conditions: C_k>0, A_k>0 showed that the established cubic equation for parameter B has three real roots: one positive, which is accepted as a solution to the problem, and two-negative. Assuming in (14), G(c)=G_M(c) we obtain a good analytical method for determining the parameter B=B(c). The calculation results for three alloys are presented in Figure 2 (solid lines). By comparing the numerical solution, marked with dots, with the approximate one solid line, we will establish a good coincidence. Deviations of about 4% are observed only in the region of the maximum value of parameter B.

Study of the pattern of changes in the invariants of deviators of stress and strain tensors in multiphase materials

Based on expression (6), the relationship between the components of local and macroscopic deformation deviators is established. Let us pass in (6) from the components of strain deviators to the components of stress deviators we obtain the relations.

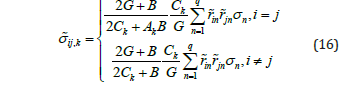
Note that in (16) both individual characteristics of phases (C_k, A_k) and global characteristics appear, which depend both on the elastic characteristics of the phases and on their volumetric content. According to [14] along with the main macroscopic coordinate system x_i^(m) in which the non-diagonal components of the deviator are equal to zero (main coordinate system), there is also a system x_i⁽ⁿ⁾ in which the diagonal components are canceled (auxiliary system). The position of the auxiliary coordinate system x_i⁽ⁿ⁾ relative to the main system x_i^(m) depends on the parameter characterizing the type of stress tensor deviator.

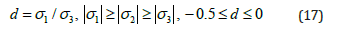
The indices for the eigenvalues σ₁,σ₂,σ₃ in (16) are assigned based on the condition that inequality (17) is satisfied. The orientation of the auxiliary coordinate system x_i⁽ⁿ⁾ relative to the main system x_i^(m) is determined by the following values of the Euler angles.

The relationship between the deviator components in the auxiliary coordinate system and the main values is determined by equalities.

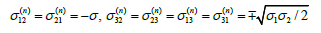
Extreme values of stress/strain deviator invariants are established based on two theorems formulated in [14].

Theorem 1: The maximum values of stress deviator invariants (A_k>1) arise in grains whose crystallographic axes are coaxial with the macrosystem with zero diagonal components and the minimum values occur in grains whose crystallographic axes are coaxial with the main coordinate system. If the opposite picture is observed.

Theorem 2: The types of deviators of stress/strain tensors in crystals with extreme values of invariants in each phase of a polycrystalline material coincide with the macroscopic type of deviator, i.e.

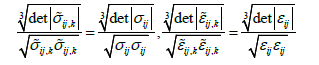
According to the formulated theorems, the invariants of A_k>1 stress/strain deviators vary within

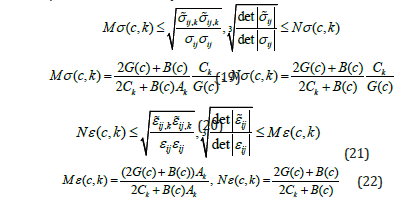
If A_k>1 then in (19),(21) the parameters M(c,k) and N(c,k) are swapped. Note that in (20) and (22) c refers to the volume fraction of the hardest phase; the volume fractions of the remaining phases are specified considering the expression Σc_k=1

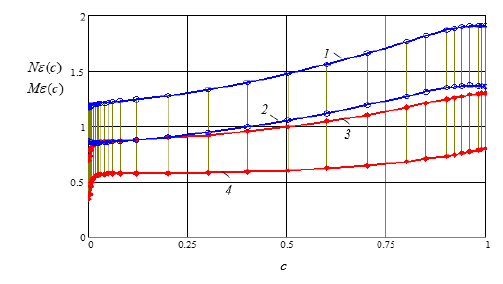
From (19), (22) it follows that the parameter B(c) has a more significant influence on the limits of change in the invariants of stress/strain deviators than the shear modulus. Due to this, the dependences for the invariants of stress and strain deviators are also nonmonotonic functions of B(c). In Figure 3 shows diagrams, Mσ (c, k) , Nσ (c, k) for the Al-Ni alloy in the Al (diagrams 3, 4) and Ni (diagrams 1, 2) phases. The shaded areas between the diagrams Mσ (c, k) , Nσ (c, k) determine the limits of relative changes in the invariants of stress deviators in the phases of the polycrystal.

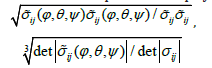
From those presented in Figure 3 diagrams show that the highest values of stress deviator invariants in the Al phase are observed at c=0.01, Nσ =1.046, Mσ = 0.904 and in the Ni phase c=0.03, Nσ = 2.544 ,Mσ =1.518. The limits of changes in stress invariants in the Ni phase are significantly greater than in the Al phase. The patterns of changes in the limiting values of the invariants of strain deviators in Al-Ni alloy grains depending on the volumetric content of the Ni phase are shown in Figure 4. From a comparison of the results obtained for stress deviators (Figure 3) and deformation (Figure 4), we find a qualitative difference. The limits of change in stress deviator invariants in the harder phase are greater than in the soft phase [15]. For deformation invariants, the opposite picture is observed. The patterns of changes in volumetric stresses and strains are established based on the postulate about the orthogonality of fluctuations of stresses and strains (4). If the postulate about the orthogonality of stress and strain fluctuations is extended to each phase, then (4), considering (5), can be represented in the form:

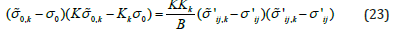
For the quantity, considering (16) we obtain the following expression (q=1,2,3)

Figure 3:Patterns of changes in the limiting values of stress deviator invariants in Al-Ni alloy grains depending on the volumetric content of the Ni phase.

Figure 4:Regularities of changes in the limiting values of the invariants of deformation deviators in grains of the Al- Ni alloy depending on the volumetric content of the Ni phase.

Both roots of equations (25) have a physical meaning. Formula (25) contains an unknown function for the macroscopic volumetric modulus of elasticity K(c). The modulus K can be determined using the principle of inconsistency of measures for spherical quantities.

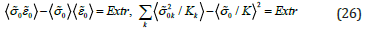
From (25) there follow two equal values of the volume σ²_0k stresses k, which determine the energy of volume change in the crystals. Because of this, in (26) σ²_0k we will take the average value of the energy of volume change. By squaring (25) for each root and adding the resulting expressions, after simple transformations we obtain.

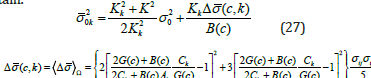
When integrating by the factor of orientation of crystallographic coordinate systems, formulas (9) were used. Considering (25) in (26) we establish the following expression for determining the bulk elastic modulus (the term Δσ (c, k) does not depend on K).

Note that the value

is the volumetric modulus of elasticity obtained within the framework of the assumption of uniformity of strain 0k 0 ε =ε , and the value

is the volumetric modulus of elasticity obtained within the framework of the assumption of homogeneity of stresses 0k 0 σ =σ . Consequently, the bulk modulus of elasticity of a multiphase polycrystal obtained from the condition of the extremum of the mismatch of measures is equal to the geometric mean value of the moduli obtained in two limiting cases: uniform stressed and uniform deformed states ( K = Kσ .Kε

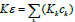
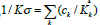
In Figure 5 shows diagrams of changes in the limiting values of volumetric stresses in the Ni phase in the Al-Ni alloy, depending on the volume content, c calculated based on formula (25). Curves 1 and 2 correspond to a positive root, and curves 3 and 4 to a negative root. Diagrams 1 and 3 0 0 ( )n σ →σ refer to Ni crystals the orientation of the crystallographic axes relative to the main macroscopic coordinate system is determined by the following values of the Euler angles ϕ =π / 4 , θ =π / 2 , ψ =α and diagrams 3, 4- ϕ =θ =ψ = 0 0 0 ( )m σ →σ under uniaxial tension (t11=20MPa). The region of changes in volumetric stresses depending on the orientations of crystallographic coordinate systems is shaded in brown. Curve 5 in Figure 5 determines the dependence of the width of the zone of changes in volumetric stresses depending on the volumetric content c. From those presented in Figure 5 diagrams show the non-monotonic nature of changes in volumetric stresses from c. At the volumetric content of nickel in the solid phase, c=c*=0.01 maximum volumetric stress occurs 0 11 σ =1.8t and minimal 0 11 σ = −0.7t . Diagrams of changes in the limiting values of volumetric stresses in the Al phase are presented in Figure 6. The numbering diagrams presented in Figure 6 are like the numbering of diagrams in Figure 5.

Figure 5:Diagrams of changes in the limiting values of volumetric stresses in the Ni phase of the Al-Ni alloy depending on the volumetric Ni content.

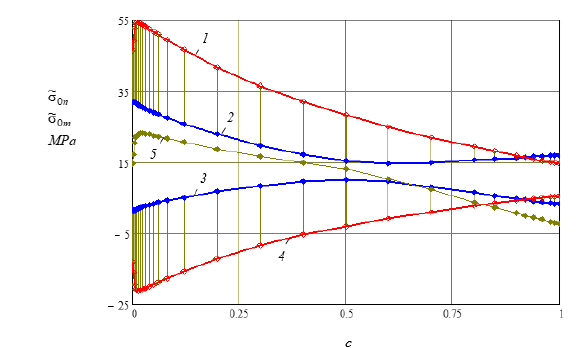
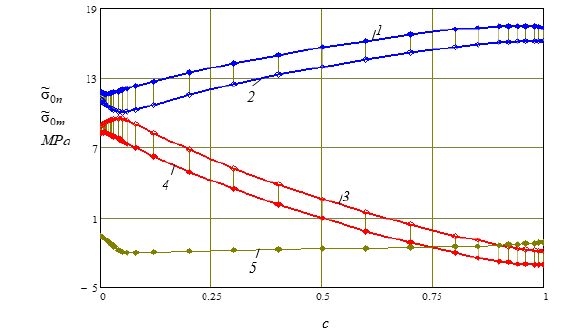
Figure 6:Diagrams of changes in the limiting values of volumetric stresses in the Al phase of the Al-Ni alloy depending on the volumetric Ni content.

Regularity of changes in deformation energy in crystals of multiphase materials

Let us consider expressions for the energy of change in shape f U and volume 0 U in crystals of a given phase of a polycrystal and a body element f U , 0 U .

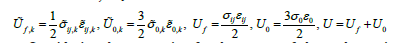
Considering the expression for the energy of shape change in (7) and (16) and considering notations (20), (22) we obtain

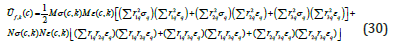
Based on equalities

To shorten the entries, the variablesϕ,θ ,ψ at rij in (26) are not indicated. According to (25) and (26), the relative energy of shape change in a given grain depends on two factors: the orientation of the crystallographic coordinate system relative to the main macroscopic system and the type of stress tensor deviator d =σ 3 /σ1 (the numbering of the axes is chosen in accordance with inequality (17)). According to the theorems formulated, limiting invariant quantities arise in grains of orientation of crystallographic systems of which (relative to the main macroscopic coordinate system) are determined by the following Euler angles: ϕ =θ =ψ = 0 ,ϕ =π / 4 ,θ =π / 2 ,ψ =α . Let us denote the energies of change in shape and volume in the coordinate system

by,

and in the system

through,

. Then from (25), (32) and (33) we obtain the following formulas for extreme values of the energy of change in shape and volume.

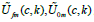
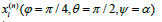
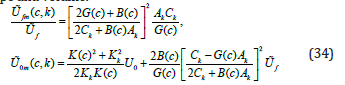
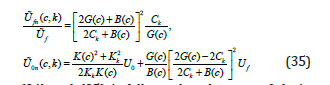
From (34) and (35) it follows that the type of deviators of the stress/strain tensors does not affect the extreme values of the shape change energy. The patterns of changes in the limiting values of the energy of shape change in crystals of the Al-Ni alloy (at Uf=1) are presented in Figure 7. Curves 1 and 2 establish the limits of variation in the energy of shape change in crystals of the Ni phase, and curves 3, 4 in the Al phase [16]. From those presented in Figure 7 diagrams show that the energy of shape change in crystals, depending on the volumetric Ni content, changes according to very complex laws. The largest value U_fn (c,k) occurs in the Ni phase at c=0.04 (max( ( , ) 1.44 ) U_fn (c,k) = U and the smallest in the Al phase at c→1. The width of the zone of change in the energy of shape change in crystals of the Al phase is greater than in crystals of the Ni phase.

Figure 7:Diagrams of changes in the energy of shape change in crystals of the Al-Ni alloy.

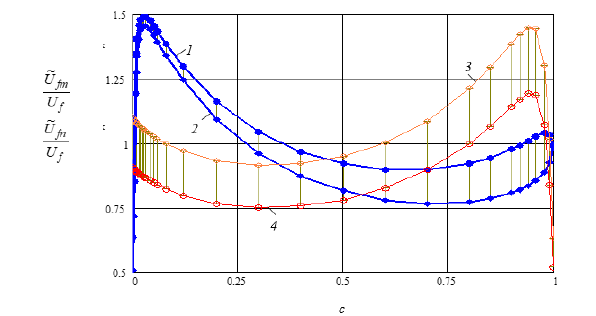
Diagrams of changes in the energy of volume change in crystals of the Al-Ni alloy are presented in Figure 8. Numerical studies show a significantly more complex nature of changes in the components of strain energy in sub elements compared to variations in stress and strain invariants. Curves 1 and 2 establish the limits of variation in the energy of volume change in crystals of the Ni phase, and curves 3, 4 in the Al phase. Note that between the patterns of variation in the energy of shape change and the energy of volume change, there is not only a quantitative but also a qualitative difference. In particular, the width of the zone of variation in the energy of volume change is significantly greater in the Ni phase than in the Al phase.

The average value of the shape change energy U_sf is determined by integration (30) over the orientation factor Ω.

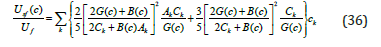
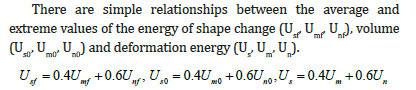
Patterns of variation in the average value of shape change energy at a constant value of the macroscopic measure of shape change energy Usf. For three alloys: Al-Cr (curve - 1), Al-Ni (curve - 2), Al-Cu (curve - 3) are shown in Figure 9. For the alloy Al-Cr, the largest relative discrepancy in the shape change energy is 0.872 at a volume content of Cr`~ 0.5 and in the Al-Ni alloy-at volumetric content Ni`~ 0.58 In the Al-Cu alloy, a monotonous increase in the mismatch of measures is observed, reaching the highest value-0.922 at volumetric content Consequently, the patterns of change in the mismatch of measures in alloys differ not only quantitatively but also qualitatively.

Figure 8:Diagrams of energy changes in the volume of Al-Ni alloy crystals.

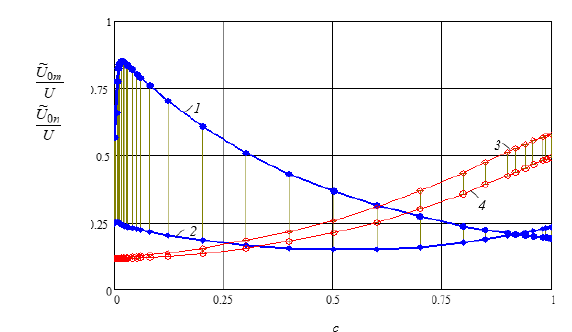
Figure 9:Patterns of variation in the average value of the shape change energy at a constant value of the macroscopic measure for three alloys: Al-Cr (curve - 1), Al-Ni (curve - 2), Al-Cu (curve - 3).

Conclusion

A system of equations is obtained based on which the influence of the concentration of phases with their mechanical properties on the macroscopic shear modulus and the heterogeneity parameter of the alloys is studied. General expressions have been established for extreme values of invariants of stress/strain deviators in polycrystal phases, which include both individual phase characteristics (anisotropy factor and crystal shear constant) and global characteristics. It is shown that when the anisotropy factor is greater than one, the maximum values of stress deviator invariants appear in grains, the crystallographic axes of which are coaxial with the macrosystem, in which the diagonal components are equal to zero, and the minimum - in grains, the crystallographic axes of which are coaxial with the main coordinate system. When the anisotropy factor is less than one, the opposite picture is observed. The nonmonotonic nature of the change in the invariants of the deviators of the stress tensors with increasing volume content of the harder component in two-phase polycrystalline materials has been established. The largest deviations of the limiting values of the invariants of the deviators of the stress tensors in the sub elements are observed at very low values of the concentration of the solid phase c~0.01÷0.06. The width of the zone of change in the limiting values of invariants increases with increasing phase anisotropy factor. The strain deviator invariant takes the greatest values in crystals with the lowest stress deviator invariant values.

Based on the principle of orthogonality of fluctuations of stress and strain tensors, a quadratic equation for volumetric stresses is obtained, the roots of which are taken as a solution to the problem. In pure macroscopic shear, the roots differ only in sign. In this case, external pressure has a nonlinear effect on the patterns of changes in the limiting values of volumetric stresses in the phases of a polycrystal. Extreme values of volumetric stresses arise in grains with extreme values of stress deviator invariants. As in the case of stress deviator invariants, the extreme values of local volumetric stresses change non-monotonically with increasing concentration of the harder phase. The patterns of changes in the energy of changes in the shape and volume of sub elements have been studied depending on the orientation factor of the crystallographic axes and the elastic characteristics of the phases. Numerical studies show a significantly more complex nature of changes in the components of strain energy in sub elements compared to changes in stress and strain invariants. The influence of the elastic characteristics of phases and their volumetric content on the discrepancy between macroscopic measures of the energy of change in shape and volume and the average values of microscopic measures is analyzed. For the Al-Cr alloy, the largest relative deviation of the shape change energy is 0.872 at the volumetric content of chromium, and for the Al-Ni alloy-at the volumetric content. In the Al-Cu alloy, a monotonic increase in the divergence of measures is observed, reaching the highest value-0.922 at volumetric content. The patterns of change in the divergence of measures in alloys differ not only quantitatively, but also qualitatively.

References

1. Marina V Yu, Marina VI (2021) Single approach to the description of the relation between micro-and macro states in reversible and irreversible deformation of polycrystals. Int Appl Mech 57(6): 707-719.
2. Trusov PV (2021) Classical and multi-level constitutive models for describing the behavior of metals and alloys: Problems and prospects (in order of discussion). News of the Russian Academy of Sciences MTT 56(1): 55-64.
3. Kroner E (1967) Elastic modulus of perfectly disordered composite materials. J Mech Phys Solids 15(5): 319-329.
4. Fokin FAG, Shermergor TD (1968) Towards the calculation of elastic moduli of heterogeneous media. PMTF 3(39): 123-129.
5. Hashin Z (1983) Analysis of composite materials: A survey. J Appl Mech 50(3): 481-505.
6. Flipona, B, Kellera C, Queyb R, Barbea FA (2020) Full-field crystal-plasticity analysis of bimodal polycrystals. International Journal of Solids and Structures 184: 178-192.
7. Marina V Yu (1987) Nonlocal approach to the problem of irreversible deformation of an inhomogeneous body, Numerical studies in continuum mechanics. Stinta, Chisinau, Moldova, pp. 47-53.
8. Marina V Yu (1997) Equations of an elastoplastic body under proportional non-isothermal loading. Applied Mechanics 6: 9-17.
9. Marina V Yu (1998) Principles of transition from micro to macro stress-strain state. News of the Academy of Sciences of Moldova, Mathematics Series 2: 16-24.
10. Hill R (1963) New derivations of some elastic extremum principles. Progress in Appl Mech the Prager Anniv Vol, New York, USA, p. 99.
11. Voight W (1982) Textbook of crystal physics, Teubner Verlag, Leipzig, Germany, p. 962.
12. Reuss A (1929) Calculation of the yield point of mixed crystals pf reason for the plasticity condition for one-term troughs. Z Angev Math and Mech 1: 49-63.
13. Shermergor TD (1977) Theory of elasticity of micro inhomogeneous media, Moscow, p. 400.
14. Marina V Yu (2023) Regularities of changing the limiting values of stress and strain invariants in micro inhomogeneous media. Mechanics of Solids 3(58): 727-747.
15. Kroner E (1963) On the physical reality of torque stresses in continuum mechanics Gauge theory with dislocations. Inst I Engng Sci 1(2): 261-278.
16. Marina V Yu, Marina VI (2020) Analysis of the relationships between local and general mechanical parameters used to describe the behavior of polycrystalline materials. Metal physics and the latest Technologies 42(3): 415-431.