- Submissions

Full Text
Evolutions in Mechanical Engineering
An Iterative Method for Solving the Problem of Diffraction of Longitudinal Shear Waves on A System of Thin Rigid Inclusions
Vsevolod Popov*
National University Odesa maritime academy, Odesa, Ukraine
*Corresponding author:Vsevolod Popov, National University Odesa maritime academy, Odesa, Ukraine
Submission: May 06, 2021;Published: June 28, 2021

ISSN 2640-9690 Volume3 Issue4
Abstract
The problem of the diffraction field determination is arising as a result of the longitudinal shear wave interaction with the thin rigid inclusions system arbitrarily situated in an infinity body was solved. Inclusions are considered to be fully coupled to the elastic medium and are moving. Unknown amplitudes of inclusions are determined from the equations of motion. The solution method is based on the submission diffraction field displacement as sum of discontinuous solutions to the Helmholtz equation, the constructed for each inclusion. As result the original problem is reduced to the system of the singular integral equations for un-known jumps of stresses on the inclusions surface, The iterative method of this system solving, where the zero approximation are the solutions of the integral equations for the single inclusions, is proposed. This integral equation for single inclusions are numerical solved the mechanical quadrature method. The final result is the approximate formulas for calculating stress intensity factors and the amplitudes of the oscillations.
Keywords: Thin ridged inclusion; Wave interaction; Integral equations; Iterative method First
Introduction
Nowadays methods of mechanics of deformable bodies (potentials method, discontinuous solutions method, etc.) make it easy to reduce the problem of determination of wave fields in a body with arbitrary numbers system of thin inclusions or cracks to the solution systems of integral equations. But as shows the analysis of the scientific publications, the main attention is paid to bodies with systems of cracks. Research of dynamic stress state bodies with systems of thin rigid inclusions is much less. One of the first works in this direction, probably should be considered [1], where is solved the problem of diffraction of waves on two parallel thin rigid incautions. Interaction of waves with periodic systems of curvilinear inclusions is considered in [2]. The method of explosive articles decisions Wave fields and Stress Intensity Factors (SIF) for elastic waves diffraction on systems of radially placed inclusions are defined of discontinuous solutions method in [3-5]. Achievements in solving dynamic problems for bodies with arbitrary systems of inclusions are associated with the development of for boundary integral equations and boundary elements methods can be seen in [6,7]. But when applying methods, based on the reducing the original boundary value problems for bodies with inclusions to systems of integral equations, there is a significant problem. It consists in the need to solve systems of integral equations of large dimension. That’s why during calculation of SIF and wave fields, authors of the limited case of a few, often just two, inclusions. Thus, the determination of dynamic stress state and wave fields in bodies with systems of thin rigid inclusions is not completely solved. In the submitted article, iterative method for determination of SIF and wave fields in the interaction of the longitudinal shear waves of N inclusions. As a result, there is no need to solve a system of N integral equations, and the N single equations are solving on each iteration. These equations correspond to a single inclusion and differ only i the right side.
Statement of the Problem
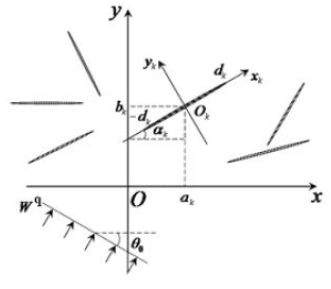
Let an elastic body that is in a longitudinal shear strain condition, N through thin rigid inclusions are situated. These inclusions are occupied on the plane Oxy by the segment’s length 2dk and with centers at points with coordinates (ak ,bk ), k =1, 2,....N (Figure 1).
The wave of longitudinal shear interacts with them which is propagated in the body and causing the following displacement along axis Oz:
Figure 1:The system of the thin ridged inclusions in the body.
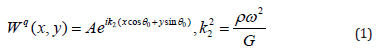
Where ω - the frequency of the oscillations, ρ , G - density and modulus of shear of the body, 0θ - the angle between the direction of propagation of the wave and the positive direction of the axis Ox. Multiplier e−iωt which determines dependency from time here and then rejected. Let W (x, y) is the only different from 0 in the conditions of longitudinal shear strain component of the vector of displacements caused by waves reflected from the defects. Then it must satisfy the Helmholtz equation

where Δ - the Laplace operator in a system of coordinates Oxy. This equation must be seen with conditions on the inclusions for the formulation that the local coordinate. systems Okxkyk connected with each of them. The relationship between the global and the local coordinate systems as well as between local coordinate systems connected with a variety of inclusions are given formulas
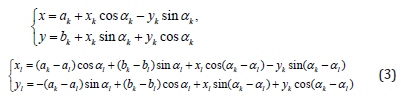
l, k =1, 2,3,....N
It is assumed that inclusion is completely coupled with an elastic medium that leads to equation
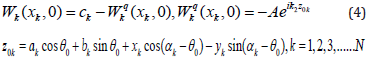
Also, the surface impurities cause a discontinuity stress unknown jumping which denomination
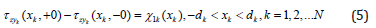
In equality (4) consists of k c -unknown displacement inclusions under the influence of propagating wave. They are determined from the equations of motion of inclusions, which in the case of harmonic oscillation are of the form
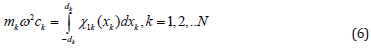
where k m -mass of k -th inclusion.
When formulated conditions the problem of determination the displacement and stress of the diffraction field in the body and SIF for inclusions is posed.
Solution of the Problem
For the solution of the problem for each inclusion with a number l in a coordinate system l l l O x y connected with it, of discontinuous solutions of equation (2) [8,9] from jumping (5) are built
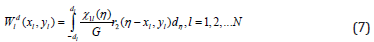
Displacement of the scattered wave field in the coordinate system Oxy is represented in the form of

Where g  are obtained from (7) as a result of the first
coordinate transformation formulas (3) for k=l. But in order to use
the formulas (8) it is necessary to determine the unknown jumps
of stress (5) on the inclusions. For determination of the unknown
jumps
are obtained from (7) as a result of the first
coordinate transformation formulas (3) for k=l. But in order to use
the formulas (8) it is necessary to determine the unknown jumps
of stress (5) on the inclusions. For determination of the unknown
jumps 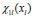 from the conditions (4) the system of integral equations
must be obtained. That the received system has received singularity
Cauchy type, (4) is replaced by the following equivalent equalities.
from the conditions (4) the system of integral equations
must be obtained. That the received system has received singularity
Cauchy type, (4) is replaced by the following equivalent equalities.
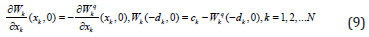
The first equality (9) is the result of applying to (4) the operation of differentiation, and the second equality is equivalence of differentiated and initial equalities. After transformations of coordinates in the (8) for other formulas (3) and substitution to (9) the following system of singular integral equations with additional conditions to determine the jumps are obtained:

In this system, introduced the notation
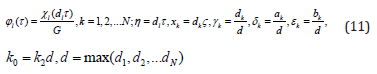
Kernels of integral operators and the right-side equations (10) are determined by the formulas.
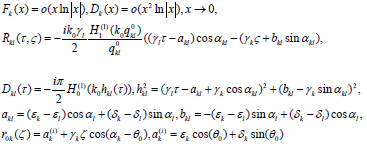
To the system (10) we must also add the equality (6) to determine the unknown amplitudes of oscillation of inclusions in the notation (11) take the form
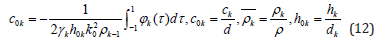
where hk,ρk are the thickness and density of the material of kth inclusion.
Iterative Method Solution
The system of integral equations (10), (12) can be solved approximately using the by the mechanical quadrature method, as i in [3-5]. But the immediate use of this method requires solving a system of linear algebraic equations, which is proportional to the number of inclusions N. Therefore, the iterative method for solving the system (12) is proposed for elimination of this problem. For this, the zero approximation is
solution of N separate equations for single inclusion
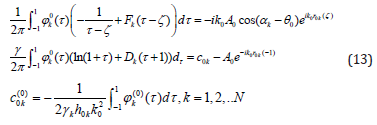
Then an iterative process continues by solving the next equations at every step

Solution of integral equations (13), (14) is based on the representation of unknown functions in the form.
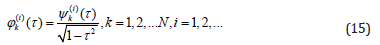
and approximation of functions of the interpolation polynomial
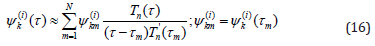
where Tn(τ) is the Chebyshev polynomial, m τ are the roots of this polynomial. The formula (15), (16) provide an opportunity to numerically solve equations (13), (14) method of mechanical quadrature’s using Chebyshev polynomials Un−1(ζ): roots
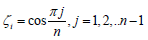
as collocation points. When applying this method known quadrature formula [10] is used for Cauchy integrals and Gauss- Chebyshev f quadrature formula [11] is used for regular integrals. To the integral with logarithmic singularity the formula obtained [3,4,9] is applied.
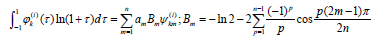
As a result, equations (14) are reduced to the solution of systems of linear algebraic equations sequence that differ only in the right sides of
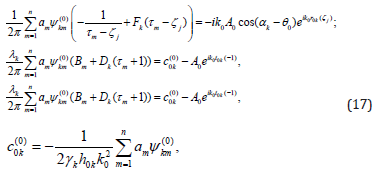
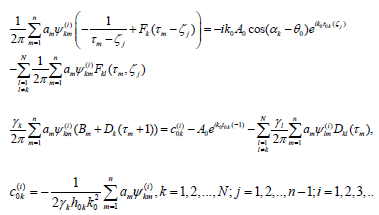
After solving this system functions 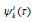 are approaching
interpolation polynomials (16). As it is known [12] stresses in the
body around the thin rigid inclusions are defined by asymptotic
formulas.
are approaching
interpolation polynomials (16). As it is known [12] stresses in the
body around the thin rigid inclusions are defined by asymptotic
formulas.

where (r, θ) are polar coordinates with the pole in right or left
end of the inclusion. The coefficients 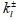 are usually called Stress
Intensity Factors (SIF) for inclusions. After solving the system (17)
their approximate value by results of the ith iteration are calculated
on formulas
are usually called Stress
Intensity Factors (SIF) for inclusions. After solving the system (17)
their approximate value by results of the ith iteration are calculated
on formulas
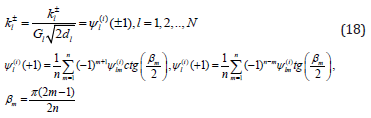
Results of Numerical Analyses
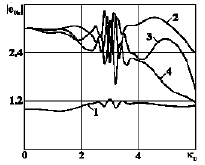
One of the main purposes of the numerical analysis was to study practical convergence of iterative method is proposed. This was a system with three inclusions of the same length 2d is considered, Inclusion is placed at the sides of the proper triangle with sides long 4d, as shown in Figure 2 The thickness and density of the inclusions [13].
There are considered to be the same: 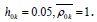 It was
assumed that plane wave of longitudinal shear, propagating
along the positive direction of the axis
It was
assumed that plane wave of longitudinal shear, propagating
along the positive direction of the axis 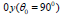 interacts with
inclusions. The Figure 3 shows the dependency graphs of absolute
value of the dimensionless SIF
interacts with
inclusions. The Figure 3 shows the dependency graphs of absolute
value of the dimensionless SIF 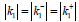 for first inclusion of
the dimensionless wave number k0 = k2d. Curve 1 corresponds to
the values SIF obtained as a result of the immediate solution of the
system of integral equations (14) mechanical quadrature method.
Curves 2.4 show the value of the SIF is obtained by the formula
(18) as a result of the implementation of the specified number of
iterations. We can see that after 4 iterations the results are obtained
by different methods almost do not differ. The continuation of the
iterative process lids to the complete coincidence of the results.
And at the frequencies of oscillations such that convergence results
is observed already after two iterations. Further the interaction of
such the waves with system of 7 inclusions Figure 4 is considered.
This system consists of inclusion at each end of which 3 radially
inclusion, which are three times less length are placed.
for first inclusion of
the dimensionless wave number k0 = k2d. Curve 1 corresponds to
the values SIF obtained as a result of the immediate solution of the
system of integral equations (14) mechanical quadrature method.
Curves 2.4 show the value of the SIF is obtained by the formula
(18) as a result of the implementation of the specified number of
iterations. We can see that after 4 iterations the results are obtained
by different methods almost do not differ. The continuation of the
iterative process lids to the complete coincidence of the results.
And at the frequencies of oscillations such that convergence results
is observed already after two iterations. Further the interaction of
such the waves with system of 7 inclusions Figure 4 is considered.
This system consists of inclusion at each end of which 3 radially
inclusion, which are three times less length are placed.
Figure 2:The system of the three inclusions.

Figure 3:Practical convergence of iterative method.

Figure 4:The system of the three inclusions.
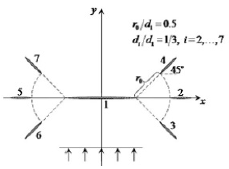
Results of calculation of SIF are shown in graphs in Figures 5 &
6. Curves 1, 2, 3, 4 in Figure 5 show the change in the absolute values of the SIF around the nearby ends of inclusions: 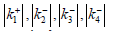 . We can see that the growth frequency (dimensionless wave
number) the monotonous increase SIF is observed for all inclusions
i, then the frequency dependence becomes oscillating. The largest
value of SIF is observed s for short inclusions inclining to long
inclusion. The graphs dependence of the absolute values of the SIF
on the dimensionless wave number (dimensionless frequency)
around the distant ends of inclusions are shown in Figure 6 Curves
with the numbers 2, 3, 4 correspond to the values
. We can see that the growth frequency (dimensionless wave
number) the monotonous increase SIF is observed for all inclusions
i, then the frequency dependence becomes oscillating. The largest
value of SIF is observed s for short inclusions inclining to long
inclusion. The graphs dependence of the absolute values of the SIF
on the dimensionless wave number (dimensionless frequency)
around the distant ends of inclusions are shown in Figure 6 Curves
with the numbers 2, 3, 4 correspond to the values 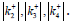 These charts show tendency of increasing SIF to reaching for the
greatest value around which oscillation is there. -We can also see
that short inclusions SIF around the distant ends significantly
exceed SIF around the nearby ends of inclusions. Curves 1-4 on
the Figure 7 illustrate the dependence of amplitude oscillations of
the appropriate inclusions
These charts show tendency of increasing SIF to reaching for the
greatest value around which oscillation is there. -We can also see
that short inclusions SIF around the distant ends significantly
exceed SIF around the nearby ends of inclusions. Curves 1-4 on
the Figure 7 illustrate the dependence of amplitude oscillations of
the appropriate inclusions 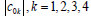 on dimensionless wave
number k0.
on dimensionless wave
number k0.
Figure 5:Absolute values of the SIF around the nearby ends of inclusions.
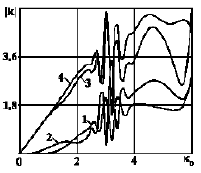
Figure 6:Absolute values of the SIF around the distance ends of inclusions.
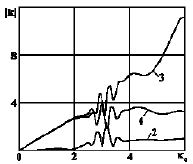
Figure 7:Dependence of amplitude oscillations on dimensionless wave number.
Conclusion
The above results allow making the following general conclusions Effective iterative method of solving the problem by definition stress condition and diffraction fields in body with arbitrary system of thin rigid inclusions at the interaction with the longitudinal shear waves. This method can be used for systems of inclusions with implicate geometry and sufficiently tightly placed inclusions. Numerical investigation has determined that the configuration of a system of inclusions, their size and relative locating substantially influence the value of the SIF. Interaction repeatedly reflected from inclusions of the waves provides dependence to SIF on the frequency of implicate shape with lots of maximums and minimums. On account of the wave interaction short and thus lighter inclusions have larger amplitude of oscillation. For inclusions with larger amplitude of oscillations also and large values of SIF are looked on. The existence of areas with a strong oscillation for frequencies such that satisfied 0 2.5 ≤ k ≤ 3.5 is common for both the SIF and the amplitude. This fact is due to effect of multiple reflection waves on the surface of inclusions at these frequencies.
References
- Jain DL, Kanval RP (1972) Diffraction of elastic waves by two coplanar parallel rigid strips. Int J Solids and Struct 10(11): 925-937.
- Nazarenko OM, Lozkin OM (2007) Plane problem of diffraction of elastic harmonic wave on periodic curvilinear inserts. Materials Science 43(2): 249-255.
- Popov VG (1996) Diffraction of elastic shear waves on radially distributed rigid inclusions. International Applied Mechanics 32(8): 624- 630.
- Popov VG (1999) Interaction of plane elastic waves with systems of radial defects. Izv RAN Мehanika tverdogo tela 4: 118-129.
- Lytvyn OV, Popov VH (2007) Interaction of plane harmonic waves with inclusions in the elastic space. Materials Science 43(3): 361-369.
- Enry Liu, Zhon Liu Zhang (2001) Numerical study of elastic wave scattering by cracks or inclusions using the boundary integral equation method. Journal of Computational Acoustics 9(3): 1039-1054.
- Jun Jei, Qingheny Yung, Sheng Wang, Thung C (2009) An investigation of dynamic interaction between multiple cracks and inclusions by TDBEM. Composites Science and Technology 69(7-8): 1279-1285.
- Popov VG (1992) Investigation of fields of displacements and stresses under diffraction of elastic shear waves on a thin rigid delaminated inclusion. Izv Ros Akad Nauk Mekh. Tverd Tela, pp. 139-146.
- Popov VG (1995) Ulanovskiy Comparative analysis of diffraction fields during the passage of elastic waves through defects of different nature. Mechanics of Solids 30(4): 93-102
- Belotserkovskiy SM, Lifanov IK (1985) Numerical methods in singular integral equations. Nauka, Moskow, Russia.
- Krylov VI (1967) Approximate calculation of integrals. Nauka, Moskow, Russia, p. 500.
- Sulym HT (2007) Bases of mathematical theory of thermoelastic equilibrium of de-formable solids with thin inclusions. Lviv, p. 716.
- Simons DA (1980) Scattering of elastic waves by thin inclusions. Journal of Ap-plied Physics 51(2): 934-940.
© 2021 Vsevolod Popov. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






