- Submissions

Full Text
Evolutions in Mechanical Engineering
Delay-Induced Synchronization on a Network of Euler’s Beams Indirectly Interconnected Via Piezoelectric Patches
Mba Feulefack SC and Nana Nbendjo BR*
Laboratory of Modelling and Simulation in Engineering, Biomimetics and Prototypes, Faculty of Sciences, University of Yaounde, Cameroon
*Corresponding author:Blaise Romeo Nana Nbendjo, Laboratory of Modelling and Simulation in Engineering, Biomimetics and Prototypes, Faculty of Sciences, University of Yaounde, Cameroon
Submission: February 14, 2020;Published: April 9, 2021

ISSN 2640-9690 Volume3 Issue3
Abstract
In this paper, Amplitude Death (AD) phenomenon is reported in a network of Euler’s beams in- directly coupled via an electrical circuit consisting of piezoelectric patches. AD phenomenon appears in this system when global synchronization of all beams takes place. The occurrence of global synchronization, which was preceded by dynamical clustering, is dependent on the size of the network as well as on the load resistance of the electrical circuit which indirectly interacts with all the beams. The results further show that the AD state can be observed for relatively very weak coupling strength and large system-size.
Keywords: Synchronization; Piezoelectric; Equilibrium; Electromechanical; Coupling
Introduction
In recent years, a great deal of interest has been devoted on exploring the complex behaviors generated from time delayed nonlinear oscillators. The interaction between the subsystems may exhibit rich forms of emergent phenomena such as: synchronization; hysteresis; phase locking; riddling; and oscillation quenching [1-3]. This great attention is due to the fact that delay is ubiquitous in a large number of dynamical systems and in different fields of application. It is well known that in the presence of time delay can induce complex phenomena on certain simple systems which do not occur in its absence. This delay can influence either negatively or positively the stability and dynamics of a system. Therefore, time delay can alter the stability of an equilibrium point, gives birth to a limit cycle, leads to bifurcation, chaos [4-7]. In structural control engineering, it is particularly important to take into account the effect of the delay in the active control of structures because its origin and influence have been shown both theoretically and experimentally. Indeed, the delay can be generated either by the time interval between the detection of the vibration by the control device and the application of the force necessary to attenuate it, or the time taken to calculate the force necessary to quench the vibration [8-10]. It seems therefore natural to include time delay in the modelling of mechanical and civil structures under control. On other hand, real world systems exhibit complex dynamics which can be described as a mutual interaction between many subsystems with different network topologies. Based on the nature of interactions among these subsystems, they can be coupled mainly in two ways: direct or indirect coupling. Resmi et al. [2] in their work presented the appearance of quenching phenomenon on a network of coupled oscillators through competing between the indirect or environmental coupling and diverse types of direct coupling as diffusive, replacement, and synaptic couplings . Quintero-Quiroz et al. [11] investigated the collective behavior of a system of chaotic Rossler oscillators indirectly coupled through a common environment. They found two collective states by varying the coupling strength: non-trivial collective behavior and dynamical clustering. Applications of network dynamics have been widely discussed in different contexts in physics, chemistry, biology, social sciences, and engineering. In the collective behaviour of real life systems, time delay is usually associated with finite propagation velocities of information signals, finite reaction times of chemicals, transportation of matter or information of electrical signals on transmission lines and so on. Time-delayed coupled dynamical oscillators can induce a large variety of dynamical phenomena such as synchronization, clustered chimera states, oscillation quenching and so on [1,12].
In this work, we intend to show the effect of time delay on a network of Euler’s beams indirectly coupled through an electrical circuit constituted of piezoelectric patches and a load resistance. The outline of this paper is as follows: In section 2, we introduce the description of a delayed network of indirectly coupled Euler’s beams through an electrical circuit and then discuss analytical results obtained from stability analysis. This is followed in section 3 by the numerical investigation of the dynamical states of the network and a global stability analysis. The effect of the delay on the synchronization state and the occurrence of SAR state is also analyzed in this section. Finally, section 3.1 is devoted to the conclusion.
Description of the Delayed Network of Indirectly Coupled Beams and Stability Analysis
System description
The system consists with a network of N simple sup- ported beams as shown in Figure 1. Each beam is assumed isotropic, uniform and flexible. We assume that all beams are identical Euler’s beams and that they are excited by a common force of amplitude f0 and frequency ω. The network of beams are interconnected indirectly through an electrical circuit. On this configuration, all the beams interact with the electrical part at the same time the dynamical state of each beam is also influenced by the electrical part. This configuration is known in the literature as indirect coupling or environmental coupling [2,11,13]. The electrical part integrates a load resistance and the capacitance of the piezoelectric patches. The piezoelectric layers are laminated along each side of both beam. Applying both continuous mechanical principles to the mechanical part and the Kirchhoff’s laws to the electrical part, the system of delayed indirectly coupled beams can be defined by the following set of equations
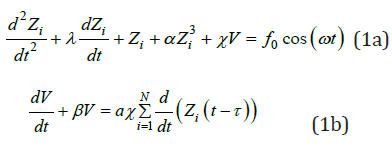
Figure 1:Schematic diagram of a feedback time delay indirectly coupled network of beams.

where the variables Zi and V represent the displacement of the ith beam and the voltage across the load resistance, respectively with i=1, 2, ..., N . χ which represents the strength of the electromechanical coupling parameter, τ which is the time delay between the detection of vibrations and the actuation feedback action of the controller, and other parameters in Eq. (1) are assumed positive throughout this work. The simulations are carried out for λ=0.39, α=0.25, β=1.24, a=318.26, ω=0.3, f0=5.0, N=20, otherwise if the values are changed, the new values will be specified. Equation (1) is obtained assuming the Euler-Bernoulli formalism with the requirements that the beam is thin and relatively long and that the torsional and axial vibrations are negligible compared to the flexural vibration. The equations modelling such a system have been established for a network of beams indirectly interconnected to an electrical circuit, without time delay consideration [14].
Linear stability analysis
To study the local stability of the equilibrium point (0,0,0), the amplitude of the external excitation is set to be f0=0.0 (autonomous case). The overall network of coupled beams are assumed to be in a synchronized state. Thus, equation (1) can be recast in the following linearized form: i i
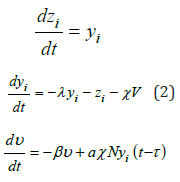
We set the Lyapunov concept by applying the fundamental solution est [9,15]. The characteristic equation related to the fixed point (0,0,0) is given in the following form:
s3 + (β + λ ) s2 + (1+ λβ + aNχ2 e−ST )s + β = 0 (3)
To obtain the stability boundary in the control parameter space (χ,β), we use the D-subdivision method [10,16]. According to this method, the stability boundary in the space of control parameters (χ,β) is determined by the points that lead either to a root s=0, or a pair of pure imaginary roots of Eq. (3). Substituting s = 0 into Eq. (3) yields:
β = 0 (4)
Setting s=ib (where b is a real parameter) into the characteristic equation (3), one finds the following system of equations:
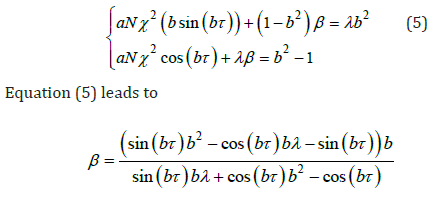 (5)
(5)
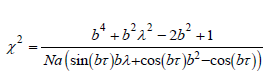 (6)
(6)
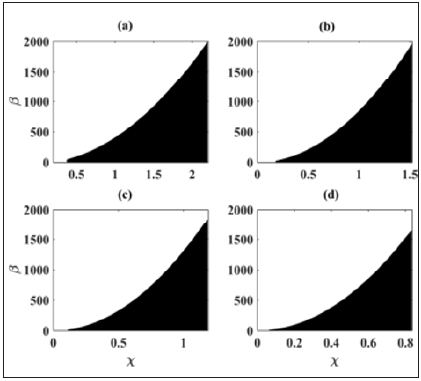
The bifurcation curve in plane (χ,β) delimiting the stability boundary can be found from the parametric equations (6) where b is varying, while assuming that the conditions χ≥0 and β≥0 are verified. Figure 2 shows the stability boundary in the parameter space χ−β for different values of the time delay. The white colour indicates the region where the whole system is stable, whereas the black colour represents the region where the system is unstable. As the time delay increases, the stable region is reduced. Thus, we lead to the conclusion the control parameters along with the time delay have an important effect on the stability and the efficiency for a control process.
Figure 2: Stability boundary in the parameter space χ-β: showing the reduction of the stable region in the system for different values of the time delay: (a) τ=0.1, (b) τ=0.2, (c) τ=0.3, (d) τ=0.5.
Effect of Time Delay on the General Behavior of the Network of Indirectly Coupled Beams
On the stability of the network
Figure 3: Bifurcation diagrams of the network of coupled beams (Eqs. (1)) depicting the local maxima of the first beam as χ increases: showing the effect of the delay τ on the occurrence.
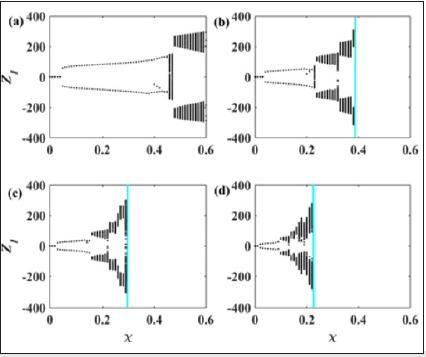
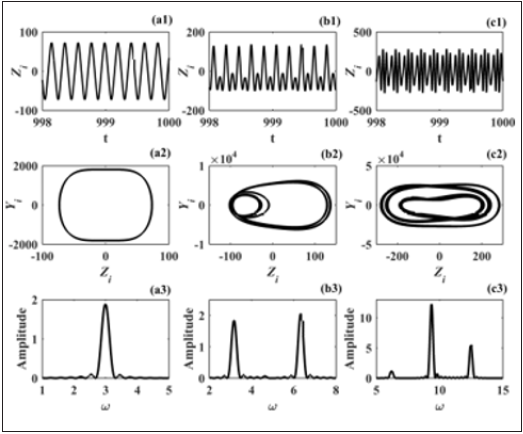
Bifurcation diagrams are plotted in order to complement the results obtained from the stability analysis. We observe the effect of the delay on the generalized behavior of the network of coupled systems as the coupling parameter increases. Figure 3 shows the bifurcation diagrams of the displacement of the first beam Z1 as function of the electromechanical coupling parameter χ for different values of the time delay τ . According to the time delay, the trajectory of the beams increases and diverges from the equilibrium point of the network of coupled beams (ye,ze)=(0,0) as the electromechanical coupling parameter increases. Moreover complex motions are observed in the network with a certain range of the coupling parameter. Nevertheless, as the coupling parameter reaches a certain value, the trajectories of all beams in the network diverge towards infinity and whole system exhibits unstable motion. Some representative time series of the displacement Zi, phase portrait and amplitude of Fourier spectra of responses of any beam in the system are shown in Figure 4 for τ=0.1 and different values of the electromechanical coupling parameter χ. As the coupling parameter χ increases, the amplitude of vibrations also increases, and the periodic oscillations observed for χ=0.1 in- volve to a period doubling motion for χ=0.45 and finally a quasiperiodic motion is observed for χ=0.55. Correspondingly, the Fourier spectra have been drawn corresponding to the time series in (Figure 4) (a3)-(b3)- (c3). The increase of χ generates several harmonics and enlarges the range of frequencies in the network. The consideration of the time delay on the feedback control of the network of beams leads to the disappearance of the strong amplitude reduction observed in the case without delay shown in [5] and brings out disturbance and instability around the system.
Figure 4: Time series, phase portrait and Fourier spectra of any beam in the network with τ=0.1 and (a) χ=0.1, (b) χ=0.45, (c) χ=0.55.
On the synchronization and strong amplitude state
In order to characterize the collective behavior of the network of coupled beams and show the effect of the time delay on the Strong Amplitude Reduction (SAR) state, we introduce the following approaches. On one hand, the occurrence of the global synchronization in the overall system of coupled beams can be numerically investigated through the asymptotic time-average ⟨σ⟩ of the instantaneous standard deviations of the distributions of state variables related to the beams [11,17], defined as
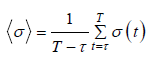 (7)
(7)
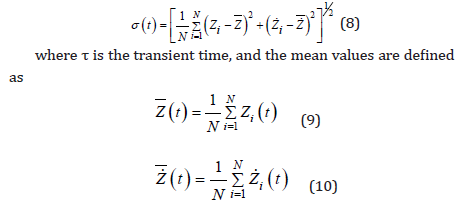
Global synchronization which describes a collective dynamic of the system of coupled beams, corresponds to the value ⟨σ⟩=0. Numerically, we consider that synchronization state is obtained as ⟨σ⟩<10−7. On the other hand, the strong amplitude reduction phenomenon is characterized with the time-average amplitude ⟨A⟩ of the displacement variables. ⟨A⟩ is calculated by the average difference between the global maximum and global minimum values of the time series of each beam of the system over a sufficient long time [13]. The average amplitude ⟨A⟩ is then written as,
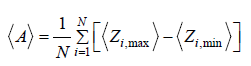 (11)
(11)
The case where ⟨A⟩∼0 is considered as strong amplitude reduction state. Thus, the average amplitude parameter can be useful to identify the coupling parameter regions for which the vibration control strategy is highly efficient. Figure 5 shows the time-average standard deviation ⟨σ⟩ of a network of indirectly coupled beams as function of the coupling strength χ for different network-sizes and with a time-delay τ=0.001. It is found that the network of coupled beams remain in a synchronization state over the coupling parameter range for small values of networksize (N≤15). As the number of coupled beams is more increased (N≥25), the synchronization state is lost for large values of the coupling strength. Furthermore, in Figure 6, the variation of the average amplitude ⟨A⟩ of the network of coupled beams, with the coupling strength χ, for different network- sizes is investigated. For small values of the network-size (N≤15), first we observe that the vibration state of the global network of coupled structures increases for small values of the coupling strength. After a threshold value of the coupling parameter, a continuous vibration reduction is observed which leads to a strong amplitude reduction state for large values of the coupling strength. Amplitude reduction is more important when the number of coupled systems increases. When the number of coupled systems grows more (N≥25), we observe at first the same behavior as in the case of small network- sizes. But for large coupling values, the average amplitude of the system increases abruptly, which means that the system becomes unstable for these values of the coupling parameter. This finding coincides with that made in Figure 5, reflecting the fact that the strong amplitude reduction state is only reached when the network of coupled beams is in a synchronization state. A global representation of the synchronization state and the average amplitude can be obtained by scanning different values of the network-sizes, N and coupling strength, χ. The time-average standard deviation ⟨σ⟩ and the average amplitude ⟨A⟩ are evaluated for different values of the time-delay. We note that these quantities are associated in each panel to the colour bars which represent the synchronization state and the global vibration state of the network of coupled beams, respectively. Figure 7 shows that the region of the global synchronization state of the network of coupled beams decreases with the increase of the delay and the number of coupled beams.
Figure 5: Time-average standard deviation σ of a network of indirectly coupled beams, under the variation of the coupling strength χ, for network-sizes N=5,10,15,25,30. With τ=0.001 and other parameters defined above.

Figure 6: Time-average amplitude A of a network of indirectly coupled beams, under the variation of the coupling strength χ, for network-sizes N=5,10,15,25,30. With τ=0.001 and other parameters defined above.
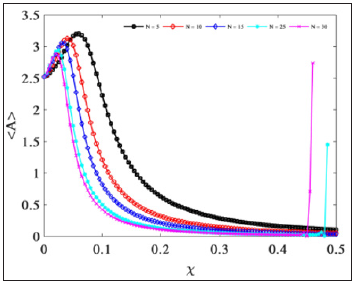
Figure 7:The schematic phase diagram of the time-average standard deviation σ in parameter space (χ, N ) for different values of the delay. (a) τ=0.001, (b) τ=0.01, (c) τ=0.1 and the other parameters are defined above.
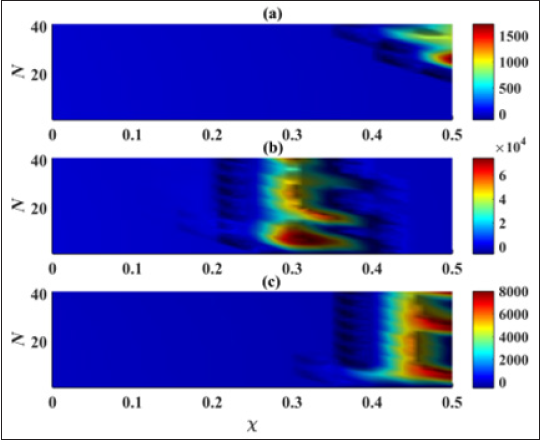
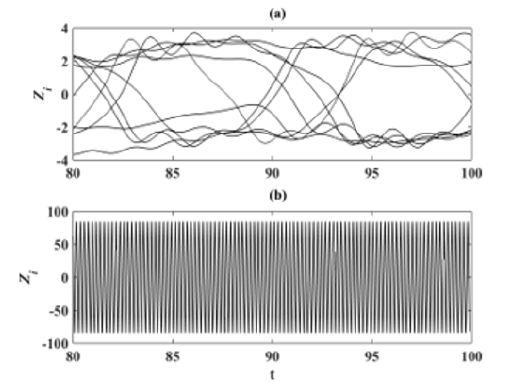
Figure 8 shows the variation of the average amplitude of the network with the increase of the delay. The dynamical states observed in (Figures 8 (a) & (b)) coincide nearly with the synchronization state of the net- work of coupled beams showed in Figures 7(a) & 7(b). The strong amplitude reduction state is represented as a part of the region in blue colours, and this state is followed by an abrupt increase of vibratory state in the overall network. For value of the time-delay τ=0.1, the strong amplitude reduction state is almost missed as showed in Figure 8(c). In this case, the large region of synchronization state observes in Figure 7(c) can be explained by the fact the beams are driven by the same external excitation. Taking into account that in a real environment, the excitation force can fluctuate from one structure to another. Thus, it seems interesting to investigate the effects of time delay on a network of coupled beams excited by heterogeneous loads. The case where the beams are excited by external loads with the same amplitude and randomly distributed frequencies such as ωi∈[0,0.5] is investigated. Figure 9 shows the effects of time delay both on the synchronization and the SAR state of a network of indirectly coupled beams, with randomly distributed external frequencies for different network-sizes and coupling strength. Both the case without delay and the with delay are considered. Thus, the network of coupled beams does not synchronize in the case without delay when a synchronization state appears on a certain range of small coupling strength as shown in Figures 9(a) & 9(b), respectively. The strong amplitude reduction state is also lost on both cases as shown in Figures 9(c) & 9(d). In order to confirm previous observations, some representative time series of the displacement Zi of a network of N=10 indirectly coupled beams are shown in Figure 10 for the case without delay (τ=0.0) and the case with delay (τ=0.1). So, the network is in de- synchronization state of the case without delay (Figure 10 (a)) while a synchronization state is observed for the case delay (Figure 10 (b)). In the last case it can be seen that the presence of the delay in the system contributes to the suppression of the complex dynamics of the network whereas the vibrations amplitude of the beams increase.
Figure 8:The schematic phase diagram of the average amplitude of the network of coupled beams A in parameter space (χ, N) for different values of the delay. (a) τ=0.001, (b) τ=0.01, (c) τ=0.1 and the other parameters are defined above.
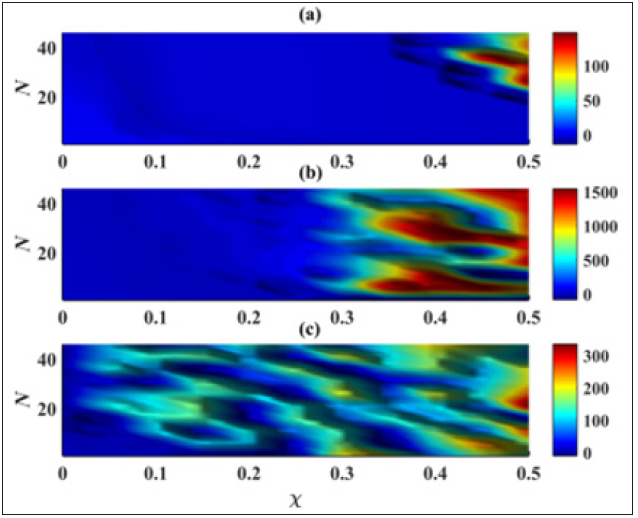
Figure 9:The schematic phase diagram of the time-average standard deviation σ for (a) τ=0.0, (b) τ=0.1, and the average amplitude of the network of coupled beams A for (c) τ=0.0, (d) τ=0.1 in parameter space (χ, N). With f0=10.0 and the other parameters defined above.
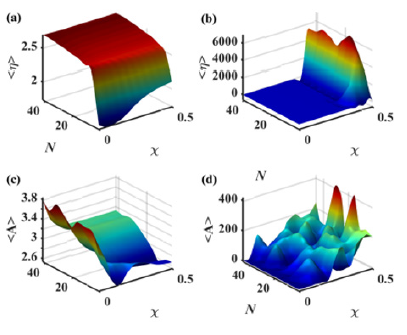
Figure 10: The schematic phase diagram of the time-average standard deviation σ for (a) τ=0.0, (b) τ=0.1, and the average amplitude of the network of coupled beams A for (c) τ=0.0, (d) τ=0.1 in parameter space (χ, N). With f0=10.0 and the other parameters defined above.
Conclusion
In this paper, we have investigated the effect of the delay on a network of indirectly coupled Euler’s beams through an electrical environment. The electrical part consists of piezoelectric patches mounted in a parallel configuration and those patches are used to absorb the mechanical energy of the network of coupled beams. An analytical analysis of stability of the overall system has been done and it has been shown that the increase of the time delay reduces the area of stable motion of the system. This has also been confirmed numerically through bifurcation diagrams and time histories. The generation of the delay in a vibration control strategy can give birth to divers dynamical states. The vibratory state and the collective dynamics of the network coupled beams have been characterized using the average amplitude function ⟨A⟩ and the time-average standard deviation ⟨σ⟩. It has been shown that the variation of the time-delay affects both the synchronization state and the strong amplitude reduction of the network of coupled beams as the coupling strength and the number of coupled structures increase. It has been observed that the large values of the delay leads the suppression of the SAR state with the increase of the coupling parameter. The vibration control strategy developed is interesting as it can be used for the spontaneous control of several mechanical structures at the same time. On other way, we have also shown that in some ways, the delay could be beneficial for the synchronization state of coupled systems.
References
- Pikovsky A, Rosenblum M, Kurths J (2001) Synchronization : A universal concept in nonlinear sciences. The Cambridge Nonlinear Science Series, Cambridge University Press, UK.
- Resmi V, Ambika G, Amritkar RE (2011) General mechanism for amplitude death in coupled systems. Physical Review E 84(4): 046212.
- Djanan AN, Nbendjo BN, Woafo P (2014) Effect of self-synchronization of DC motors on the amplitude of vibration of a rectangular plate. Eur Phys J Special Topics 223(4): 813-825.
- Atay FM (2010) Complex time-delay systems: Theory and applications. Springer, Germany.
- Jeevarathinam C, Rajasekar S, Sanjun MAF (2013) Effect of multiple time-delay on vibrational resonance. Chaos 23(1): 013136.
- Rusinek R, Weremczuk A, Kecik K, Warminski J (2014) Dynamics of a time delayed duffing oscillator. International J of Non-Linear Mechanics 65: 98-106.
- Tchakui MV, Woafo P (2016) Dynamics of three unidirectionally coupled autonomous duffing oscillators and application to inchworm piezoelectric motors: Effects of the coupling coefficient and delay. Chaos 26(11): 113108.
- Morgan R, Wang A (2002) An active-passive piezoelectric absorber for structural vibration control under harmonic excitations with time-varying frequency, part1: algorithm development and analysis. J of Sound and Vibration 124(1): 77-83.
- Nbendjo BN, Salissou Y, Woafo P (2005) Active control with delay of catastrophic motion and horseshoes chaos in a single well duffing oscillator. Chaos, Solitons & Fractals 23(3): 809-816.
- Zhang L, Yang CY, Chajes MJ, Cheng AHD (1993) Stability of active tendon structural control with time delay. J of Engineering Mechanics 119(5): 1017-1024.
- Quintero Quiroz C, Cosenza M (2015) Collective behavior of chaotic oscillators with environmental coupling. Chaos, Solitons & Fractals 71: 41-45.
- Sethia GC, Sen A, Atay FM (2008) Clustered chimera states in delay-coupled oscillator systems. Physical Review Letters 100(14): 144102.
- Verma UK, Kamal NK, Shrimali MD (2018) Co-existence of in-phase oscillations and oscillation death in environmentally coupled limit cycle oscillators. Chaos, Solitons & Fractals 110: 55-63.
- Mba Feulefack SC, Nbendjo BN, Vincent UE, Woafo P (2017) Dynamical clustering, synchronization and strong amplitude reduction in a network of Euler’s beams coupled via a dynamic environment. Nonlinear Dynamics 88(1): 455-464.
- Tuwa PN, Woafo P (2018) Analysis of an electrostatically actuated micro-plate subject to proportional-derivative controllers. J of Vibration and Control 24(10): 2020-2029.
- Kolmanovskii VB, Nosov VR (1986) Stability of functional differential equations. Elsevier, Netherlands.
- Palazzi M, Cosenza M (2014) Amplitude death in coupled robust-chaos oscillators. Eur Phys J Special Topics 223(13): 2831-2836.
© 2021 Nana Nbendjo BR. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






