- Submissions

Full Text
Evolutions in Mechanical Engineering
Effect of Transport Coefficient Modeling on Hypersonic Non-Equilibrium Flow Simulations
Xiaowen Wang*
Department of Aerospace Engineering and Mechanics, The University of Alabama, USA
*Corresponding author: Xiaowen Wang, Department of Aerospace Engineering and Mechanics, The University of Alabama, Tuscaloosa, AL 35487, Alabama, USA
Submission: September 03, 2019;Published: January 09, 2020

ISSN 2640-9690 Volume3 Issue1
Abstract
Many important scientific and engineering applications, such as strong shock and turbulence interactions and hypersonic boundary-layer stability and transition, involve strong shocks and high temperature effects. These processes are strongly nonlinear and proven to be very complex to understand with existing tools. The most widely used shock capturing methods may incur numerical oscillations near the shock and may not be accurate enough for numerical simulations of hypersonic boundary-layer stability and transition problems. To solve such problems, a unique approach of using high-order shock-fitting method is adopted, where the shock is treated by shock-fitting method as a sharp boundary. However, there are no reported studies on the effects of transport coefficient modeling, chemical reaction rate and equilibrium constant modeling, internal energy mode modeling, and energy relaxation modeling. In this paper, the effect of transport coefficient modeling on hypersonic non-equilibrium flow simulations is considered using the recently developed high-order shock-fitting solver. The study is carried out by comparing numerical simulations with experimental datasets. The results consistently show that an increase of Lewis number leads to a decrease of shock standoff distance. For low and moderate enthalpy cases, different models of transport coefficient lead to minor change in shock standoff distance and flow field. Nevertheless, the pressure difference indicates that for pressure sensitive problems such as hypersonic boundary-layer stability and transition, one still needs to consider the effects of transport coefficient models.
Introduction
Hypersonic flow is categorized by certain physical phenomena that do not typically play an important role in subsonic and supersonic flows. These effects could be thin shock layers, entropy layers, viscous-inviscid interactions, and high temperature gas effects [1]. All these effects need to be considered for scientific and engineering applications involving strong shocks, such as strong shock and turbulence interactions [2-4] and hypersonic boundarylayer stability and transition [5-7]. At temperatures up to 500-800K, gas flow stays calorically perfect. Only translational and rotational energy modes are fully excited while the excitations of vibration energy mode and chemical reactions are negligible. As a result, specific heat capacities remain constant. For temperatures in the range of 800-2000K, vibration energy mode takes an important role in sharing the total energy with the translational and rotational modes. Near the lower temperature limit of this regime, translation-vibration energy relaxation between harmonic oscillator molecules dominates because most of the molecules are near the ground vibrational state. Near the higher limit of this regime, vibration-vibration energy relaxation becomes significantly active because not only are vibrationally excited molecules highly populated, but also vibration-vibration energy relaxation is considerably faster than its translation-vibration counterpart. Also, the vibrational oscillation becomes inharmonic as the temperature approaches the dissociation level. However, results within the harmonic oscillator approximation are known to be sufficiently accurate for most practical purposes [8].
For temperatures above 2000-2500K, vibration energy mode is fully excited and O2 starts dissociating. Around 4000K, O2 is completely dissociated and N2 starts dissociating. When the temperature reaches 9000k, most of the N2 is dissociated. Coincidentally, this is the temperature where dissociated N and O atoms become ionized. Around 12000K, all the gases are completely dissociated and about 14% of them are ionized such that there is a sufficient amount of free charges. Radiation emitted and absorbed by the gas can become important and could eventually modify the energy distribution in the flow field. At 20000K, double dissociation begins. And finally, when it reaches 30000K, the gas is completely ionized [9]. This regime corresponds to M∞ greater or much greater than 30.
All high temperature effects are due to molecular collisions which occur at finite rates. When the collision rates are much faster than flow rates, it is called as “equilibrium flow”. On the other hand, if the collision rates are much slower than flow rates, it is called as “frozen flow”. Unfortunately, these two situations cannot completely describe the hypersonic flow over a space/air vehicle. There will always be regions where the collision rates are in the same vicinity of the flow rates. Moreover, different species will have different reaction rates and different energy relaxation rates. Therefore, energy transfers between bulk kinetic energy, translational energies, chemical energies, and vibration energies of different species are actively in progress in a hypersonic thermochemical non-equilibrium flow. When these effects start to play dominant roles, the flow is called “non-equilibrium flow”.
In the past years, interest in various types of vehicles in hypersonic flow regime produced numerous structured grids based non-equilibrium flow solvers. According to recent publications, Laura, DPLR, and Lore are the most frequently referenced and are intensively validated against each other [10] and against wind tunnel tests. LAURA (Langley Aerothermodynamic Upwind Relaxation Algorithm) is mainly developed by Peter Gnoffo at the NASA Langley Research Center [11-14]. It uses Roe’s flux difference splitting scheme with Yee’s second-order symmetric total variation diminishing scheme to model the inviscid fluxes. Steady state solution is obtained using either point or line relaxation time integration scheme. The vibration energy mode is assumed to be in equilibrium with the electronic energy, and the translational energy is assumed to be in equilibrium with the rotational energy mode. The code supports multi-block structured grids and MPI communication for massive parallel computing. DPLR (Data- Parallel Line Relaxation) is initially developed at University of Minnesota by Wright et al. [15]. It is further developed at NASA Ames research center [10]. DPLR implicit method is optimized for efficient parallel computing by arranging the body normal dependent data with local CPU in order to perform the relaxation process simultaneously in parallel mode. DPLR uses third order modified Steger-Warming flux splitting scheme with MUSCL data reconstruction to model the inviscid fluxes. Unlike LAURA, the vibration energy mode is separately treated from the electronic energy modes, and the translational energy is assumed to be equilibrium with the rotational and electronic energy mode. It also supports multi-block structured grids. Lore [16] was developed at the Advanced Operations and Engineering Services Group in Europe. The flow solver uses modified AUSM scheme with MUSCL data reconstruction to achieve second-order accuracy coupled with a van Albada limiter. Time advancement to a steady-state solution is achieved using an alternating direction line Gauss-Seidel implicit relaxation method. The code supports multi-block structured grids. This code covers a wide range of flight regimes from subsonic to hypersonic.
However, the most widely used shock capturing methods may incur numerical oscillations near the shock and may not be accurate enough for numerical simulations of hypersonic boundary-layer stability and transition. To solve problems including strong shocks and thermochemical non-equilibrium phenomena, a unique approach of using high-order shock-fitting method is proposed. The main shock is treated by the shock-fitting method as a sharp boundary. The shock dynamics is governed by shock jump conditions so that the interaction of the main shock with freestream disturbance is computed accurately. The main advantages of the shock-fitting method are its uniform high-order accuracy for flow containing shock waves and no spurious oscillations near the shock. On the contrary, most of the popular shock-capturing methods are only first-order accurate at the shock and may incur spurious numerical oscillations near the shock. The shock-fitting solver is implemented based on 5-species chemistry set of air and a two-temperature model. It is assumed that translational and rotational energy modes are in equilibrium at translational temperature whereas vibration energy, electronic energy, and free electron energy are in equilibrium at vibration temperature. The flow solver uses fifth-order shock-fitting method of Zhong [17] with local Lax-Friedrichs flux splitting.
However, there are no reported studies on the effects of transport coefficient modeling, chemical reaction rate and equilibrium constant modeling, internal energy mode modeling, and energy relaxation modeling. In this paper, the effect of transport coefficient modeling on hypersonic non-equilibrium flow simulations is considered using the recently developed highorder shock-fitting solver. The study is carried out by comparing numerical simulations with published experimental datasets.
Models of Transport Coefficients
The governing equations, high-order numerical methods, and models for thermochemical non-equilibrium flow used in the current study have been discussed in another paper [18]. One can refer to it for more details. Since the goal is to study the effect of transport coefficient modeling on hypersonic non-equilibrium flow simulations, two regularly used models of transport coefficients are implemented to the code. At first, the viscosity of each species is calculated from the following curve fits (Model I). For the five species air, coefficients of curve fits are listed in Table 1, with the original data being obtained from Candler’s dissertation [19].
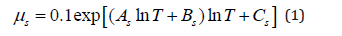
By combining the viscosity of each species, the total viscosity is calculated as
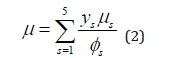
Heat conductivities of each species corresponding to translation temperature and vibration temperature are calculated as
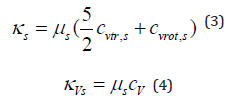
Table 1: Curve fit coefficients of 5-species air viscosity.

Total heat conductivities are calculated from species heat conductivities in a way similar to calculating total viscosity from species viscosities,
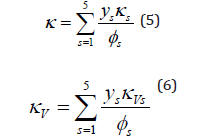
In equations (2) to (6),
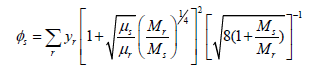
The diffusion coefficient is determined by assuming a constant Lewis number,

To investigate the effect of Lewis number, extra simulations based on a constant Lewis number of 0.25 is also considered.
A more complex model of transport coefficients is then applied (Model II) [20]. According to this model, transport coefficients are calculated as follows,
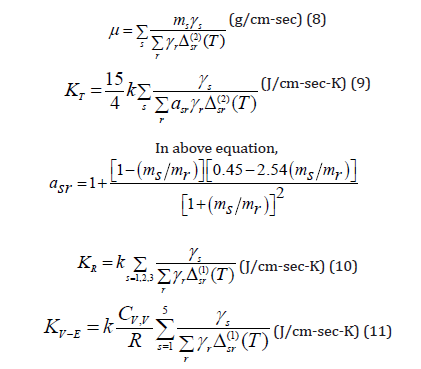
To calculate viscosity and heat conductivity, from equation (8) to equation (11), the collision terms are as follows,
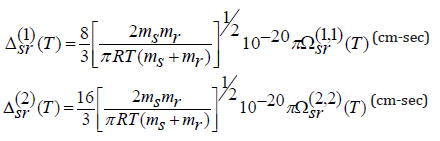
Collision integrals involving neutrals (Non-Columbic collision integrals) are
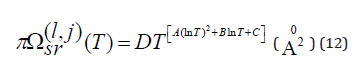
Species diffusion coefficients are defined as,
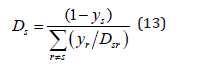
where ys is the molar fraction. For binary diffusion between heavy particles,
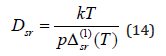
Result and Discussion
The effect of transport coefficient modeling on hypersonic nonequilibrium flow simulations are considered for two- and threedimensional experiments. The flow conditions and mesh structures are listed below. For the two published experiments ([21,22]), freestream velocities are on the same order of magnitude. Therefore, specific total enthalpy of the flow is mainly determined by pressure and density. Higher pressure and lower density lead to a higher specific total enthalpy. Figure 1 indicates that specific total enthalpy of hypersonic flows increases from Lobb’s experiment to Hornung’s experiment. Later, the two experiments are referred to as low enthalpy case and moderate enthalpy case.
Figure 1: Flow conditions and mesh structures of the two cases of simulations.

Air flow over a sphere
In this case, the flow over a sphere corresponding to Lobb’s experiment [21] is tested. The same flow has been numerically studied by Candler et al. [19]. Numerical simulation results are compared with Lobb’s experimental measurement.
Figure 2 shows that shock standoff distance obtained from the current numerical simulation has a very good agreement with the experimental measurement of Lobb, which also indicates that the non-equilibrium models are accurately implemented to the highorder shock-fitting method. Figure 3 compares pressure contours for three cases of simulations (Mode I with Lewis number being 0.25 and 1.4 and Mode II). It shows that pressure contour does not change significantly for different models of transport coefficients. The edge of pressure field again shows that shock standoff distance does not change significantly for different models of transport coefficients.
Figure 2: Comparison with Lobb’s experiment: shock standoff distance.

Figure 3: Comparison of pressure contours for three cases of simulation.
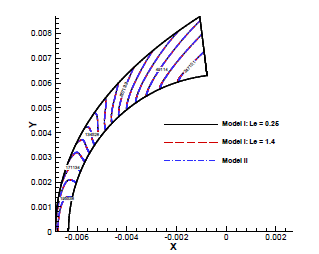
Figure 4 shows temperature contours of the simulation based on Mode II of transport coefficients. The dramatic difference between translation temperature and vibration temperature shows non-equilibrium phenomenon in the flow field. However, for this low enthalpy case, the temperatures are not that high.
Figure 5 shows a comparison of shock standoff distance and the pressure difference contour between the simulations using different transport coefficients. Although the difference in shock standoff distance is minor, Figure 5a shows that the increase of Lewis number leads to a decrease of shock standoff distance. However, the usage of Mode II of transport coefficients leads to a slight larger shock standoff distance. Figure 5b shows the pressure difference between simulations (Model I with Lewis number being 0.25 and Model II) is up to 3.34%. The result indicates that for pressure sensitive problems such as hypersonic boundarylayer stability and transition, where the disturbances are general about the magnitude 10-5 of the mean flow, one definitely needs to consider the effects of transport coefficient models.
Figure 4: Temperature contours of the simulation based on Mode II.

Nitrogen flow over 1-inch radius cylinder
In this case, the nitrogen flow over a cylinder corresponding to Hornung’s experiment [22] is tested. This flow has a moderate total enthalpy. The shock standoff distance of numerical simulation has been verified in a previous paper [23]. Figure 6 compares pressure contours for three cases of simulations (Mode I with Lewis number being 0.25 and 1.4 and Mode II). It shows that pressure contour and shock standoff distance do not change significantly for different models of transport coefficients for the moderate enthalpy case. Figure 7 shows temperature contours of the simulation based on Mode II of transport coefficients. Non-equilibrium phenomenon in the flow field is also shown. However, for this moderate enthalpy case, the temperatures are still not that high.
Figure 5: Comparison of shock standoff distance and pressure difference contour.
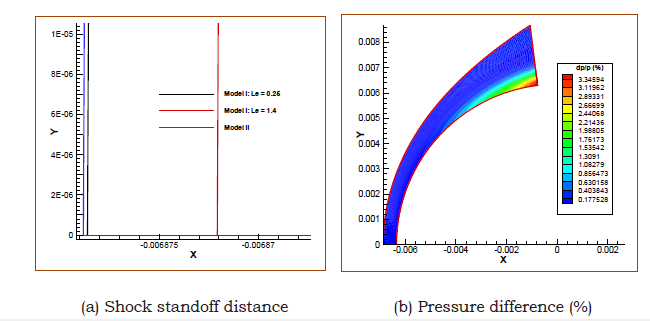
Figure 6: Comparison of pressure contours for three cases of simulation.
Figure 7: Temperature contours of the simulation based on Mode II.
Figure 8 shows a comparison of shock standoff distance and the pressure difference contour between the simulations using different transport coefficients. Figure 8a again shows that the increase of Lewis number leads to a decrease of shock standoff distance. However, the usage of Mode II of transport coefficients leads to an even smaller shock standoff distance. Figure 8b shows the pressure difference between simulations (Model I with Lewis number being 1.4 and Model II) is up to about 1.0%. The result also indicates that for pressure sensitive problems such as hypersonic boundary-layer stability and transition, where the disturbances are general about the magnitude 10-5 of the mean flow, one needs to consider the effects of transport coefficient models.
Figure 8: Comparison of shock standoff distance and pressure difference contour.
Summary
In this paper, the effect of transport coefficient modeling on hypersonic non-equilibrium flow simulations is considered using the high-order shock-fitting non-equilibrium flow solver. The code is implemented based on a two-temperature model. In the computer code, the 5-species chemistry set of air is implemented. The effect of transport coefficient modeling on hypersonic non-equilibrium flow simulations are considered for two- and three-dimensional problems. The results consistently show that an increase of Lewis number leads to a decrease of shock standoff distance. For low and moderate enthalpy cases, different models of transport coefficient lead to minor change in shock standoff distance and flow field. Nevertheless, the pressure difference indicates that for pressure sensitive problems such as hypersonic boundary-layer stability and transition, one still needs to consider the effects of transport coefficient models.
References
- Anderson JD (1998) Hypersonic and high temperature gas dynamics. McGraw-Hill, USA.
- Rawat PS, Zhong X (2010) On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions. Journal of Computational Physics 229(19): 6744-6780.
- Rawat PS, Zhong X (2010) Numerical simulation of strong shock and turbulence interactions using high-order shock-fitting algorithms. Bulletin of the American Physical Society 55(16).
- Lele SK, Larsson J (2009) Shock-turbulence interaction: What we know and what we can learn from peta-scale simulations. Journal of Physics: Conference Series 180(012032).
- Wang X, Zhong X (2005) Receptivity of a Mach 8 flow over a sharp wedge to wall blowing suction. AIAA paper 2005-5025.
- Wang X, Zhong X (2012) Numerical simulation and experiment comparison of leading-edge receptivity of a Mach 5.92 boundary layer. AIAA paper 2006-1107, 2006.
- Wang X, Zhong X (2009) Effect of wall perturbations on the receptivity of a hypersonic boundary layer. Physics of fluids 21 (044101).
- Vincenti WG, Kruger CH (1967) Introduction to physical gas dynamics. Krieger Publishing Co, Krieger Lane/Malabar, Florida, USA.
- Mannella GG (1966) Chemical reactions in electrical plasmas. The OHIO Journal of Science 66(3): 334-339.
- Wright MJ, Olejniczak J, Walpot L, Raynaud E, Magin T (2006) A code calibration study for Huygens entry aero heating. AIAA 2006: 0382.
- Gnoffo PA, Mccandless RS, Yee HC (1987) Enhancements to program LAURA for computation of three-dimensional hypersonic flow. AIAA 1987-0280.
- Gnoffo PA (2001) Computational aerothermodynamics in Aero assist applications. AIAA 2001-2623.
- Gnoffo PA (2003) Computational fluid dynamics technology for hypersonic applications. AIAA 2003-3259.
- Hash D, Olejniczak J, Wright MJ, Dinish P, Pulsonetti M, et al. (2007) FIRE II calculations for hypersonic nonequilibrium aerothermodynamics code validation: DPLR, LAURA, and US3D. AIAA 2007-0605.
- Wright MJ, Candler GV, Bose D (1998) Data-parallel line relaxation method for the navier–stokes equations. AIAA Journal 36(9): 1603-1609.
- Walpot L (2002) Development and application of a hypersonic flow solver. TU Delft University, Netherlands.
- Zhong X (1998) High-order finite-difference schemes for numerical simulation of hypersonic boundary-layer transition. Journal of Computational Physics 144(2): 662-709.
- Wang X (2017) Non-equilibrium effects on the stability of a Mach 10 flat-plate boundary layer. AIAA Paper 2017-3162.
- Candler GV (1988) The computation of weakly ionized hypersonic flows in thermo-chemical nonequilibrium. Stanford University, California, USA.
- Gupta RN, Yos JM, Thompson RA, Lee KP (1990) A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 K. 1990, NASA Reference Publication 1232.
- Lobb RK (1964) Experimental measurement of shock detachment distance on spheres fired in air at hyper velocities, in the high temperature aspects of hypersonic flow. In: Nelson WC (Ed.), MacMillan Co, New York, USA.
- Hornung HG (1972) Non-equilibrium dissociating nitrogen flow over spheres and circular cylinders. Journal of Fluid Mechanics 53(1): 149-176.
- Wang X, Zhong X (2009) Nonequilibrium and reactive high-speed flow simulations with a fifth order WENO scheme. AIAA Paper 2009-4041.
© 2020 Xiaowen Wang. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






