- Submissions

Full Text
Evolutions in Mechanical Engineering
On Soliton Solutions of the Drinfeld-Sokolov- Wilson System by He’s Variational Principle
Mohammed K Elboree*
Department of Mathematics, Egypt
*Corresponding author:Mohammed K Elboree, Department of Mathematics, Egypt
Submission: November 29, 2018; Published: April 4, 2019

ISSN 2640-9690 Volume2 Issue4
Abstract
The aim of this paper is to obtain the traveling wave solutions for the Drinfeld-Sokolov-Wilson system by He’s semi-inverse variational principle which includes the solitary and periodic wave solutions by a suitable choice for the parameters. We analysis these solutions physically by some gores to complement this study. Finally, this method can be used successfully for solving integrable and nonintegrable equations.
Keywords: He’s semi-inverse variational principle; Traveling wave solutions; Dronfield-Sokolov-Wilson system; Soliton solutions; Periodic wave solutions
Introduction
Nonlinear partial differential equations (NLPDEs) is used to describe many important phenomena in mathematical physics, mechanics, chemistry, biology, etc. Such as Cortège de Vries equation, Burgers equation, Schrodinger equation, Bossiness equation and so on. So, the discovery of the exact solutions of nonlinear partial differential equations is of the most important priorities. Many effective methods are used to construct traveling wave solutions of NLPDEs, among of these methods, Adomian decomposition method [1], the homotropy perturbation method [2], the variational iteration method [3, 4], the He’s variational approach [5], the extended homoclinic test approach [6, 7], homogeneous balance method [8-11], Jacobi elliptic function method [12-15], Baclund transformation [16, 17], G0=G expansion method [18] . He’s semi-inverse variational principle is used to obtain the traveling wave solutions for Dronfield-Sokolov-Wilson system which include the solitary and periodic wave solutions by a suitable choice for the parameters.
It is important to point out that a new constrained variational principle for heat conduction is obtained recently via the semi-inverse method combined with separation of variables[19], which is an exactly the same with He-Lee’s variational principle[20] a short remark on the history of the semi-inverse method for establishment of a generalized variational principle is given in [21]. In soliton theory, we aim to search for the solitary wave solutions for NLPDEs using various methods [22]. In particular, we used in this paper the variational principle, which enables us to and the Lagrangian for the Drinfeld-Sokolov-Wilson system, which related to the conservation laws which plays an important role in solution process [23,24] and provides physical insight into the nature of the solution of this problem as shown by gures. Also, this method helps in establishing connections between the physics and mathematics and much more active than the Noether’s theorem [25, 26].
The key idea in this paper is to use the He’s semi-inverse variational principle to and out several exact solutions for Drinfeld-Sokolov-Wilson system. Conclusions is given in the last of this paper.
Methodology
Suppose we are given a nonlinear partial differential equations (NLPDEs) in the following form

where x and t are the independent variables.
This method can be summarizing as follows
A. By using the wave solutions
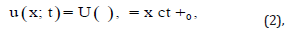
we can transform Eq. (1)
into an ordinary differential equation (ODE)
N(U; cU ; U ; cU ; :::) = 0
B. Integrating Eq. (2) and setting the integration constants equal to zero for simplicity.
C. Construct the Lagrangian in the following form according to the He’s semi-inverse method,

where L is a Lagrangian for the Eq. (2)
D. By a Ritz method [27], one can obtain a different forms of solitary wave solutions, such as
U( )= Asech (B); U( ) = Acsch (B); U( ) = A tanh (B); ss
and so on. In this paper, we concentrate to obtain a solitary wave solution in the form
U( )= Asech (B) (4)
where A and B are constants to be determined.
Substituting Eq. (4) into Eq. (3) and making I stationary with respect to A and B results in

We can obtain A and B by solving Eqs. (5) and (6). Therefore, we can construct the solitary wave solution for Eq. (4)
Soliton solutions to Drinfeld-Sokolov-Wilson system
We aim in this section to obtain the soliton solutions for the Drinfeld-Sokolov-Wilson system
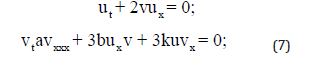
where a; b and k are constants [28].
By using the transformation
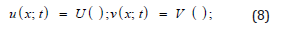
where = x ct + 0, c; 0 are constants.
Substituting Eq. (8) into Eq. (7), we and that

where the prime denotes to the derivative with respect to the variable a, b, c and k are constants. Integrating Eqs. (9), we obtain the relation between the variables V (), U () as follows

Substituting V () in Eqs. (9), we obtain after integration and setting the constant of integration zero for simplicity
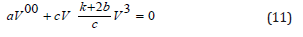
According to [29], by He’s semi-inverse variational principle [3], we can obtain the following variational formulation
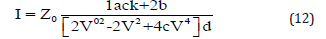
According to the Ritz-like method, we search a solitary wave solution in the form
V ( ) = Asech (B ) (13)
Substituting Eq. (13) into Eq. (12), we have
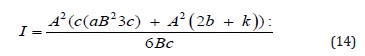
To and the constants A and B, we solve the following equations
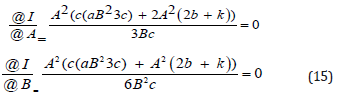
From Eqn. (15), we get

Therefore, the solitary wave solutions for Drinfeld-Sokolov- Wilson system constructed as follows
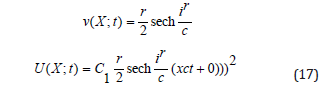
For a suitable choice for a parameter in Eq. (17), Figure 1 & 2 describes the shape of solitons for waves u (x; t) and v (x; t) respectively (Figure 1)
Figure 1:The soliton solution of Eq. (17).
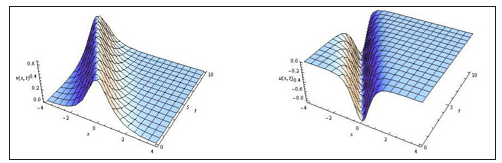
Figure 2:The soliton solution of Eq. (17).

For another constant A and B in Eq. (16) (Figure 2)
We search another soliton solution in the form [30]
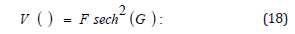
where F and G are constants to be determined. Substituting Eq. (18) into Eq. (12), we obtain
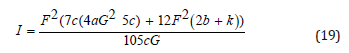
To and the constants F and G, we solve the following equations (19)
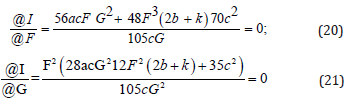
From Eqn. (20), we get
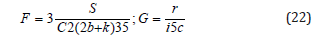
For a suitable choice for a parameter in Eq. (22), Figure 3 & 4 describes the shape of solitons for waves u (x; t), and v (x; t) respectively for another constant F and G in Eq. (21)
Figure 3:The soliton solution of Eq. (22).
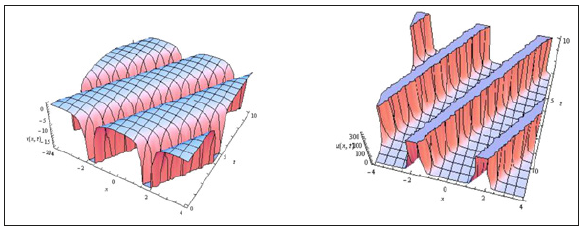
Figure 4:The soliton solution of Eq. (22).
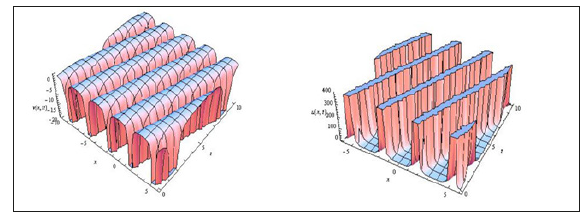
Physical Discussions
In this section, we discusses the physical explanation of the solutions obtained for the Drinfeld-Sokolov-Wilson system (7), namely (17), (22) which are soliton pattern solutions caused by the delicate balance between nonlinearity effect V3 and dispersion effect V1000 which have an infinite tails and keep their form and velocity after an entire interaction with others solitons. We display the time evolution of these solutions by some gores to describe the dynamical properties in 3D graphs in Figure 1-4 are the forth solutions (22).
We note the wave speed c acts a critical role in a physical structure of the solutions for Drinfeld-Sokolov-Wilson system. The 3D graphs in Figure 1-4 show the shape of propagation of soliton solutions (17) and (22) for the Drinfeld-Sokolov-Wilson system (7).
Result and Discussion
He’s semi-inverse variational principle was used to obtain the traveling wave solutions for Drinfeld-Sokolov-Wilson system including new type of solitary wave solutions. He’s variational principle is a very dominant instrument to and the soliton solutions for various nonlinear equations in mathematical physics and may be important for the explanation of some practical physical problems. This method is a powerful mathematical tool for solving other nonlinear evolution equations arising in mathematical physics. This method makes the underlying idea clear and not darkened by the unnecessarily by complicated form of mathematical expression. Also, we can combine the well-known method such as Jacobi elliptic function method and exp-function method with He’s semi-inverse variational method, but they need a mathematical software, and this method is extreme simplicity and concise results for a wide range of NLPDEs compared with the Noether’s theorem.
References
- Abbasbandy S, Darvishi MT (2005) A numerical solution of Burgers’ equation by modified Adomian method. Applied Mathematics and Computation 163(3): 1265-1272.
- Ji-Huan He (2005) Application of homotropy perturbation method to nonlinear wave equations. Chaos, Solitons and Fractals 26(3): 695-700.
- Ji-Huan He (2004) Variational principles for some nonlinear partial differential equations with variable coefficients. Chaos Solitons Fractals 19(4): 847-851.
- Darvishi MT, Khani F, Hamedi NS, Ryu SW (2010) New modification of the HPM for numerical solutions of the sine-Gordon and coupled sine- Gordon equations. Int J Comput Math 87(4): 908-919.
- Naja H, Naja M, Arbabi MA (2012) New soliton solutions for Kaup- Boussinesq system. Internat J Appl Math Research 1(4): 402-408.
- Darvishi MT, Mohammad N (2011) A modification of extended homoclinic test approach to solve the (3+1)-Dimensional potential-YTSF equation. Chin Phys Lett 28(4): 040202.
- Mohammad N, Maliheh N, Darvishi MT (2012) New exact solutions to the (2+1)-Dimensional Ablowitz-Kaup-Newell-Segur equation: Modification of the extended homoclinic test approach. Chin Phys Lett 29(4): 040202.
- Mohammed K (2009) New exact traveling wave solutions of the (3 + 1) dimensional Kadomtsev-Petviashvili (KP) equation. Commun Nonlinear Sci Numer Simul 14(4): 1169-1175.
- Mohammed K (2009) Exact traveling wave solutions of the Boussinesq- Burgers equation. Math Comput Model 49(3-4): 666-671.
- Abdel Rady AS, Osman ES, Mohammed K (2010) The homogeneous balance method and its application to the Benjamin-Bona-Mahoney (BBM) equation. Appl Math Comput 217(4): 1385-1390.
- Abdel RAS, Osman ES, Mohammed K (2010) On soliton solutions for a generalized Hirota-Satsuma coupled KdV equation. Commun Nonlinear Sci Numer Simul 15(2): 264-274.
- Abdel RAS, Mohammed K (2010) On soliton solutions for Boussinesq- Burgers equations. Commun Nonlinear Sci Numer Simul 15(4): 886-894.
- Abdel RAS, Khater AH, Osman ES, Mohammed K (2009) New periodic wave and soliton solutions for system of coupled Korteweg-de Vries equations. Appl Math Comput 207(2): 406-414.
- Saad ZR, Mohammed K (2010) New periodic wave and soliton solutions for a Kadomtsev-Petviashvili (KP) like equation coupled to a Schrödinger equation. Commun Nonlinear Sci Numer Simul 15(10): 2818-2827.
- Mohammed KE (2012) New soliton solutions for a Kadomtsev- Petviashvili (KP) like equation coupled to a Schrödinger equation. Appl Math Comput 218(10): 5966-5973
- Abdel RAS, Osman ES, Mohammed K (2009) Multi soliton solution for the system of Coupled Korteweg-de Vries equations. Appl Math Comput 2101: 177-181.
- Abdel RAS, Osman ES, Mohammed K (2010) Multi-soliton solution, rational solution of the Boussinesq-Burgers equations. Commun Nonlinear Sci Numer Simul 15(5): 1172-1176.
- Mohammed K, Elboree (2012) Hyperbolic and trigonometric solutions for some nonlinear evolution equations. Commun Nonlinear Sci Numer Simul 17(11): 4085-4096.
- Tao ZL, Chen GH (2013) Remark on a constrained variational principle for heat conduction. Thermal Science 17 (3): 951-952.
- Fei DD (2013) A short remark on He-Lee’s variational principle for heat conduction. Thermal Science 17(5): 1561-1563.
- Li XW (2013) On the semi-inverse method and variational principle. Thermal Science 17(5): 1565-1568.
- Hassanabadi H, Zarrinkamar S, Hamzavi H, Rajabi AA (2012) Exact solutions of d-dimensional klein-gordon equation with an energydependent potential by using of Nikiforov-Uvarov method. Arab J Sci Eng 37(1): 209-215.
- Mehdi A, Yasir Khan (2013) Nonlinear dynamic analysis of conservative coupled systems of mass-spring via the analytical approaches. Arab J Sci Eng 38(1): 155-162.
- Johnpillai AG, Khalique CM (2011) Conservation laws of KdV equation with time dependent coefficients. Commun Nonlinear Sci Numer Simulat 16(8): 3081-3089.
- Naz R (2012) Conservation laws for some compacton equations using the multiplier approach. Appl Math Lett 25(3): 257-261.
- Ahmad Y, Al Dweik (2012) On the conservation laws for a certain class of nonlinear wave equation via a new conservation theorem. Commun Nonlinear Sci Numer Simulat 17(4): 1566-1575.
- Ritz WJ, (1909) About a new method for solving certain variation problems of mathematical physics. J fr die Reine und Angew Math 1909(135): 1.
- Hirota R, Grammaticos B, Ramani A (1986) Soliton structure of the Drinfel’d-Sokolov-Wilson equation. J Math Phys 27(6): 1499.
- He JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Modern Phys B 20(10): 1141-1199.
- Ye YH, Mo LF (2009) He’s variational method for the Benjamin-Bona- Mahony equation and the Kawahara equation. Comput Math Appl 58(11-12): 2420-2422.
© 2019 Mohammed K Elboree. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






