Piezoelectric Material Non-Linear Characteristics, Compensation Methods and Application

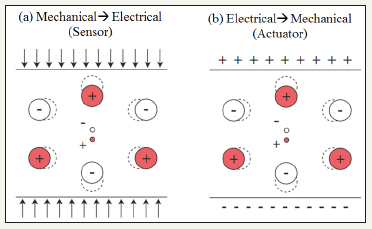
Piezoelectric material has been widely used as sensor and actuator in many applications such as in structural vibration reduction [1-3], control of flexible structures [4,5], positioning control [6,7] and energy harvesting [8]. This is due to the piezoelectric effects which converted the mechanical energy to the electrical energy (i.e., sensing ability) and conversely from electrical energy to the mechanical energy (i.e., actuating ability). These piezoelectric effects were firstly discovered but only been used in 1940 (Figure 1a & 1b). Show both of the piezoelectricity working principle of sensing and actuating abilities, respectively. From these Figure 1a & 1b, the first effect is due to the mechanical stress which transfers the energy to the electrical charge across the material and the second effect is conversely due to the applied electrical charge to the material resulting in mechanical stress [9].

The detail of piezoelectric constitutive equations in the stresscharge form are given by:

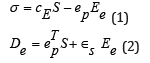
Where S is the strain, σ is the stress, D_e is the electric displacement, E_e is the electric field strength, ep is the piezoelectric coupling coefficient in the stress-charge form, c_E contains stiffness coefficients under constant electric field and ϵ_S is the electric permittivity matrix under constant strain. Subscripts E indicates zero or constant electric field and σ is the zero or constant stress field, while superscript T denotes matrix transposition. Piezoelectric actuators are known for their various shapes, flexibility, high frequency response and high stiffness but very limited on displacement [10-12]. Thus, they are suitable for the vibration isolation of stiff structures. For example, piezoelectric actuator has been used to control the vibration in automotive [13,14], aerospace [1,15], robotic [7] and civil structures [16].

Figure 1:Sensing and actuating abilities from piezoelectric effect [10].

Non-linear hysteresis and creep are the inherent characteristic of the piezoelectric actuator, which affect their performance and these characteristics will be described in the next section. In general, there are three types of piezoelectric materials which can be used as an actuator such as ceramics, polymers or composites. Poly vinylidene fluoride (PVDF), Lead Zirconate Titanate (PZT) and Lithium Niobate (LN) are the examples of piezo polymer, piezo crystal and piezo composite, respectively [17]. All of them can be used as an actuator due to their characteristics which are lightweight and flexible and suitable for many applications. From all these materials, PZT (i.e., ceramic material) is still the most widely used material compared to the PVDF and LN due to lower voltage consumption for the actuation process [12]. Piezoelectric actuators in the market are available in various prices and shapes.

The price depends on the complexity, size and function of the piezoelectric actuator. In term of shape, there are many types of piezoelectric actuators that have been developed, such as stack, patch, bender, tube and shear-type piezo actuators [18]. The force and displacement of the actuator depend on the diameter and length, respectively. The high blocking force of the piezo stack actuator made it suitable for the control of instrumentation such as rotors and fuel injector. For example, two piezo stack actuators were used as control actuators in the Active Vibration Control (AVC) of the rotating machines for both steady-state and transient motions [19]. For the rail diesel engine, piezo stack actuator is used to actuate the fuel injector resulting in improved efficiency and emission reduction [20].

Piezoelectric actuator suffers from the non-linear hysteresis which can negatively affect its performance. Hysteresis is defined as a dynamic lag phenomenon between the input voltage and output displacement or force of the piezoelectric actuator in the time domain operation [12]. The hysteresis characteristic of the piezoelectric actuator was noticeable when operating in the large voltage range with slow or fast speed motion, which can bring about large positioning error [10]. The hysteresis of the piezoelectric actuator occurred in both static and dynamic operations. Figure 2 shows the typical hysteresis curve of the piezoelectric actuator when operating in open-loop condition. From the Figure 2, there are two mechanisms to characterize the hysteresis of the piezoelectric actuator; displacement and voltage. When the piezoelectric actuator was energized, the displacement of the piezoelectric actuator will move from the position 1 to position 2 with the maximum supplied voltage of 50V and return back to the position 1 when the piezoelectric actuator was de-energized.

However, the increment route (from position 1 to position 2) and the decrement route (from position 2 to position 1) are not the same due to the hysteresis effect. This effect become worse when operating the piezoelectric actuator in a larger voltage range as shown by position 3 (i.e., maximum voltage of 75V) and position 4 (i.e., maximum voltage of 100V) in Figure 2. To date, many of dynamic models have been developed to predict the hysteresis behavior of the piezoelectric actuator. The models can be categorized in two types which is operator-based control and differential-based control.

Figure 2:Typical hysteresis curve of an open-loop piezoelectric actuator [12].

For operator-based hysteresis models, such as Prandtl- Ishlinski, Preisach and Preisach have successfully model the hysteresis and a lot of works have been reported. Generally, it involves the integration models which the kernel has infinite number of hysteretic operators, which can describe hysteresis shape accurately. Whereas, differential-based models such as Duhem and Bouc-Wen models are alternate in modelling this non-linear characteristic. In this approach, the model will have finite dimensional and easily extended to continuous input using approximation and a limited process that avoid computation time [21-25]. The advantage and disadvantages of the different types of hysteresis models are summarized as in Table 1.

Table 1:List of the compensation methods for hysteresis characteristics.

Figure 3:Step response of the piezoelectric actuator with displacement difference resulted from the hysteresis [34].

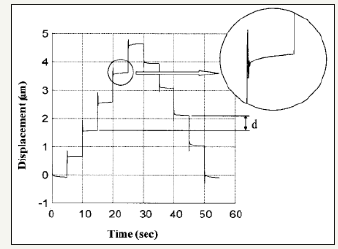
Onward, the fundamental task is to exploit the characteristics of these models and design the corresponding control that can mitigating the hysteresis effect [26-31]. Another non-linear characteristic of the piezoelectric actuator to be considered is a creep. It can define as phenomena with displacement drift without accompanying change in input voltage [32]. It appears as effect of piezoelectric viscoelastic material properties and also exist in both electrical and mechanical domains [33]. Found that constant input voltage lead to displacement creep of the piezoelectric as shown in Figure 3. The highlight circle shown clearly the creep effect in piezoelectric application [34]. Clearly, the presence of the creep can cause substantial errors especially in atomic force microscopes [35-37] and micro-manipulators [38].

In some applications, the creep effect can be removed using the sensor technology, but it will limit the performance especially for micro or nano-positioning applications. Nevertheless, the cost for the sensor with high accuracy and high bandwidth are very expensive and large in size such as interferometers, optical sensors and camera-microscope measurement systems [39]. Concerning the creep, there are several methods have been proposed. One of them is logarithmic function. The method aims to compensate the creep by having an opposite logarithmic model applied to the voltage so the final strain will remain constant. Another method to be considered is a dynamic operator. The method is composed of many elementary first order operators. The advantage and disadvantages of the different types of creep compensation methods are summarized as in Table 2.

Table 2:Comparison of different type of compensation method for creep.

In closed-loop method, it offers several advantages like accuracy, repeatability and vibration rejection. Indeed, it is an expensive option, whereby there is a requirement of sensor to be used. Second option (open loop) is a low-cost compensation method, whereby it does not used the sensor, but it subjected to low accuracy and problem in the reliability of the data. Based on the previous study, both closed and open loop share one limitation, only can be used for 1-DOF problems [40,41].

Non-linear hysteresis and creep are the inherent characteristic of the piezoelectric material which can negatively affect its performance. There are plenty of models that have been developed to characterize this characteristic of the piezoelectric actuator. This problem can be compensated using the method listed above. Future works should concentrate on other non-linear characteristics of the piezoelectric material and advanced control strategies to compensate them for the application as sensor and actuator in the AVC system.

1. Mallick R, Ganguli R, Bhat MS (2014) An experimental and numerical study of piezoceramic actuator hysteresis in helicopter active vibration control. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 228(5): 690-705.
2. Mystkowski A, Koszewnik AP (2016) Mu-synthesis robust control of 3D bar structure vibration using piezo-stack actuators. Mech Syst Signal Process 78: 18-27.
3. Tůma J, Šimek J, Škuta J, Los J (2013) Active vibrations control of journal bearings with the use of piezo actuators. Mech Syst Signal Process 36(2): 618-629.
4. Saad MS, Jamaluddin H, Mat Darus IZ (2015) Online monitoring and self-tuning control using pole placement method for active vibration control of a flexible beam. J Vib Control 21(3): 449-460.
5. Bruant I, Proslier L (2015) Improved active control of a functionally graded material beam with piezoelectric patches. J Vib Control 21(10): 2059-2080.
6. Zheng J, Fu M (2013) Saturation control of a piezoelectric actuator for fast settling-time performance. IEEE Transactions on Control Systems Technology 21(1): 220-228.
7. Choi SB, Seong MS, Ha SH (2013) Accurate position control of a flexible arm using a piezo actuator associated with a hysteresis compensator. Smart Mater Struct 22(4): 402.
8. Hurlebaus S, Gaul L (2006) Smart structure dynamics. Mech Syst Signal Process 20(2): 255-281.
9. Chandrasekaran S, Lindner DK (2000) Power flow through controlled piezoelectric actuators. J Intell Mater Syst Struct 11(6): 469-481.
10. Wu Y, Culter S, Pannozzo G, Leang K, Devasia S (2008) Modeling and control of smart actuators: Integrating nano/bio technology into ME curriculum. ASEE Annual Conference and Exposition, USA, pp. 1-22.
11. Sohn JW, Paeng YS, Choi SB (2010) An active mount using an electromagnetic actuator for vibration control: Experimental investigation. Proc Inst Mech Eng Part C J Mech Eng Sci 224(8): 1617-1625.
12. (2009) Physik instrumente. Piezo Nano Positioning.
13. Kunze H, Riedel M, Schmidt K, Bianchini E (2003) Vibration reduction on automotive shafts using piezoceramics. Proceeding of SPIE, The international Society for Optical Engineering 5054: 382.
14. Teoh CY, Mohdripin Z (2017) Dither effect on drum brake squeal. J Vib Control 23 (7): 1057-1072.
15. Sabatini M, Gasbarri P, Monti R, Palmerini GB (2012) Vibration control of a flexible space manipulator during on orbit operations. Acta Astronaut 73: 109-121.
16. Song G, Sethi V, Li HN (2006) Vibration control of civil structures using piezoceramic smart materials: A review. Eng Struct 28(11): 1513-1524.
17. Nakamura N (2012) Ultrasonic transducers: Materials a design for sensors, actuators and medical applications. Woodhead Publishing Limited, Cambridge, United Kingdom.
18. (2018) Piezo transducers: Flexure actuators, piezo stacks, tubes, bimorph benders, shear actuators. PI Motion & Positioning.
19. Simões RC, Steffen V, Der Hagopian J, Mahfoud J (2007) Modal active vibration control of a rotor using piezoelectric stack actuators. J Vib Control 13(1): 45-64.
20. Satkoski CA, Shaver GM, More R, Meckl P, Memering D (2009) Dynamic modelling of a piezoelectric actuated fuel injector. IFAC Proceedings Volumes 42(26): 235-240.
21. Omer A, Mohany A (2014) The effect of high frequency vortex generator on the acoustic resonance excitation in shallow rectangular cavities. Can Acoust Acoust Can 42(3): 16-17.
22. Al Janaideh M, Feng Y, Rakheja S, Su SY, Rabbath CA (2009) Hysteresis compensation for smart actuators using inverse generalized Prandtl-Ishlinskii model. American Control Conference, pp. 307-312.
23. Hassani V, Tjahjowidodo T, Do TN (2014) A survey on hysteresis modeling, identification and control. Mech Syst Signal Process 49(1-2): 209- 233.
24. Deng L, Tan Y (2003) Modeling of rate-dependent hysteresis in piezoelectric actuators. Proceedings of the IEEE International Conference on Intelligent Robots and Systems, pp. 978-982.
25. Rakotondrabe M (2012) Classical Prandtl Ishlinskii modeling and inverse multiplicative structure to compensate hysteresis in piezoactuators. American Control Conference, pp. 1646-1651.
26. Hu H (2002) On the classical Preisach model for hysteresis in piezoceramic actuators. Mechatronics 13(2): 85-94.
27. Park JKN, Washington GN (2004) Prediction of hysteretic effects in PZT stack actuators using a hybrid modelling strategy. The International Society for Optical Engineering (5383): 48.
28. Lin CJ, Lin PT (2012) Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput Math with Appl 64(5): 766-787.
29. Gomis BO, Ikhouane F, Montesinos M (2008) Control of Bouc Wen hysteretic systems: Application to a piezoelectric actuator. International Power Electronics and Motion Control Conference, pp. 1670-1675.
30. Habineza D (2016) Multivariable generalized Bouc Wen modelling, identification and feedforward control and its application to multi-DoF piezoelectric actuators. IFAC Proceedings 47(3): 10952-10958.
31. Miri N, Mohammadzaheri M, Chen L (2013) A comparative study of different physics-based approaches to modelling of piezoelectric actuators in EEE/ASME. International Conference on Advanced Intelligent Mechatronics. Mechatronics, pp. 1211-1216.
32. Changhai R, Lining S (2005) Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sensors Actuators A: Phys 122(1): 124-130.
33. Wood RJ, Steltz E, Fearing RS (2005) Nonlinear performance limits for high energy density piezoelectric bending actuators. In Proceedings IEEE International Conference on Robotics and Automation, pp. 3633- 3640.
34. Jung H, Shim JY, Gweon DG (2000) New open-loop actuating method of piezoelectric actuators for removing hysteresis and creep. Rev Sci Instrum 71(9): 3436-3440.
35. Salapaka S, Sebastian A, Cleveland JP, Salapaka MV (2002) High bandwidth nano-positioner: A robust control approach. Rev Sci Instrum 73(9): 3232.
36. Sebastian A, Salapaka S (2003) H∞ loop shaping design for Nano-positioning. In Proceedings of the American Control Conference, pp. 3708- 3713.
37. Croft N, Shed G, Devasia S (2001) Creep, hysteresis, and vibration compensation for piezo actuators: Atomic force microscopy application. J Dyn Syst Meas Control 123(1): 35.
38. Goldfarb M, Celanovic N (1997) Modelling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst 17(3): 69-79.
39. Rakotondrabe M (2012) Modelling and compensation of multivariable creep in multi-DOF piezoelectric actuators in Proceedings. IEEE International Conference on Robotics and Automation, pp. 4577-4581.
40. El Rifai OM, Youcef T (2002) Creep in piezoelectric scanners of atomic force microscopes. Proc Am Control Conf 5: 3777-3782.
41. Rakotondrabe M, Clévy C, Lutz P (2010) Complete open loop control of hysteretic, creeped, and oscillating piezoelectric cantilevers. IEEE Trans Autom Sci Eng 7(3): 440-450.