- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Evolutions in Mechanical Engineering
Anomalous Diffusion Through Homopolar Membrane: One-Dimensional Model
Guilherme Garcia Gimenez1 and Adélcio C Oliveira2*
1 Discente de Engenharia Mecatrônica e bolsista pela FAPEMIG, Universidade Federal de São João del Rei, Brazil
2 Departamento de Estatística, Física e Matemática, Universidade Federal de São João del-Rei, Brazil
*Corresponding author:Adélcio C Oliveira, Departamento de Estatística, Física e Matemática, Universidade Federal de São João del-Rei, Campus Alto Paraopeba-Ouro Branco, MG, Brazil
Submission: September 11, 2018;Published: October 16, 2018
ISSN: 2640-9690Volume1 Issue3
Abstract
We investigate the stationary state solution of the fractional diffusion equation applied to Electrodialysis. This model corresponds to the anomalous diffusion case, that has several applications on Biology, Chemistry and Engineering. With the tools of fractional calculus, we have obtained the analytical solution for the fractional diffusion equation considering an external field. We use the mean field approximation to obtain the solution.
Keywords:Anomalous diffusion; Electrodialysis; Fractional calculus; Membranes; Mean field approximation
Introduction
Electrodialysis is an electrochemical separation process that uses ion-selective membranes as separation agents. Therefore, electrodialysis is a technique in which the separation of substances is accelerated by the application of an adequate electric field. In this way, the ions are transported through these membranes from one solution to another, by means of an electric field as a driving force, without the need of the addition of chemical reagents. Then, cation and anion membranes are organized alternately, to form dilute and concentrated flows between the membranes. In a recent work, [1] stated the electroneutrality condition can be understood as the fixed and mobile charge have, both, a local null charge. However, this condition is not valid for the entire process of electrodialysis separation and it is not a necessary condition, instead of electroneutrality, [2,3] have shown that Mean Field Approximation reproduce better the well-known behavior of polarization curve of electrodialysis membrane. In this work, we investigate the validity of the Mean Field Approximation with the aid of a fractional calculation to analyze the ionic transport through a membrane. This correspond to the anomalous diffusion case [4]. The anomalous diffusion models have a lot of applications in Biology and Medicine Peng et al. [5]; Paiva et al. [6]; Hidalgo & Tello [7], Physics, Astrophysics and Seismology Combe et al. [8]; Wegler [9]; Hughes [10], just to cite a few examples.
Mathematical Model for Anomalous Diffusion
There are many approaches to anomalous diffusion, and also many mathematical definitions of it, see [4] and references there in. The most widely used is a time dependent stochastic process of random variable x which the mean square displacement is a linear function of time (t) , for t 0 , i.e. x2 ≈ Dtα ,α determines the diffusion type, if α =1 normal diffusion, α < 1 sub-diffusion and α >1 super-diffusion. An important approach to anomalous diffusion is obtained by the porous media equation [11], it is given by:
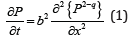
where is the probability density, and is a constant with dimension of (Time)(Length)α/2. is related with by the Tsallis-Bukman scaling law [12],
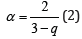
the stationary solution of Eq. (1) for an initial delta function is given by:
where p N is a normalizing constant that depends on q A [11]
and q A is a fit parameter that depends on q . The distribuition Eq.
(3) is the so called q-Gaussian, that is due to the fact that is the
usual Gaussian. It is
usual to define the
Anomalous Electrodialysis Diffusion Model
In this section, we use the transport equation for the separation process in a cell, where a constant electric field ( ) E is applied in the studied system. In a recent work, [4] suggested that, since the mean field approximation E = E0, i.e. constant in space directions, was used to support the non-electroneutrality condition, the study should focus on transport in stationary state. To perform the analyzes, we consider that the ions are immersed in a fluid that can be modeled by a diffusion term. In this way, we use the equation and continuity of Nerst-Plank, where the flow of particles can be expressed, in dimensionless form, as:
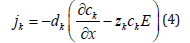
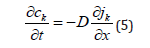
where is an arbitrary scale factor, and all variables and fields are defined in a dimensionless form. Thus, is the dimensionless flux density of the ion, is the diffusion coefficient of ion divided by, is the ion concentration, is the ion valence, is the time, is the position in a opposite direction of the membrane’s surface scaled by the membrane thickness. We are interested in the steady state, so we use the fractional equation similar to the stationary equation for the diffusion with Mean Field Approximation, given by: We are interested in the steady state, so we use the fractional equation similar to the stationary equation for the diffusion with Mean Field Approximation, given by:
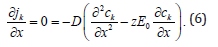
For a general case using ck= u (t) y (x) then:,
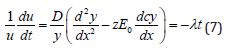
where λ > 0 ,λ =w2/D. Thus, for the spatial part, we will have:
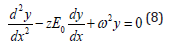
Thus, the equivalent fractional equation will be given by:
where k = −zE0 , ò∈(0,1] and x∈[0, L]. Therefore, to solve the Eq. (9) we will make use of the Laplace Transform. In this way:
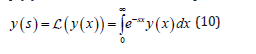
Then, term by term, we have:
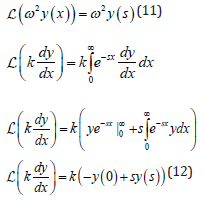
For the fractional term, we have:
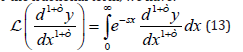
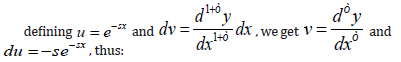
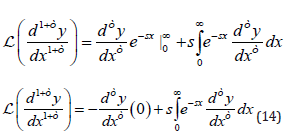
Finally, the integration can be obtained by (Camargo & Oliveira, 2015) as:
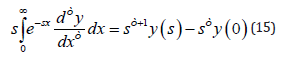
Therefore, after applying the Laplace Transform in all terms of Eq. (9), we have:
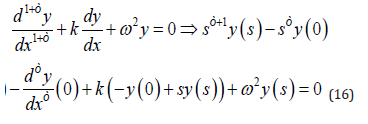
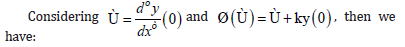
The solution can be obtained by inverting Eq. (17), we use the result of [13], where we have:
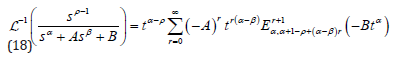
where Euα,β(z) is the three parameter Mittag-Leffler [14-18]. Finally, we can write Eq. (17) as:
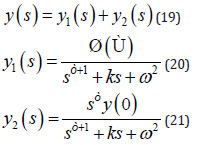
Now, using Eq. (18), we obtain y1 (s) as:
then
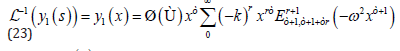
For y2 (s) we get:
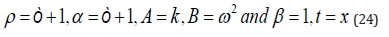
and we have:
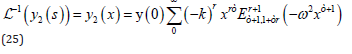
Finally, the general solution is:
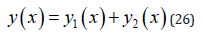
a. Case =1 and k = 0
First we consider only the case ò =1. In this way, the Eq. (9) is now:
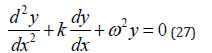
then, the solution can be obtained in a form y = erx . The characteristic polynomial is:
with Δ = k2 − 4ω2 and with three possible cases, Δ > 0 , Δ < 0 and Δ = 0 . Then solution is:
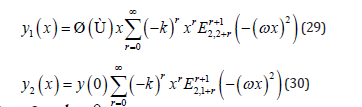
b. Case k = 0
Now, considering k = 0 , we have:
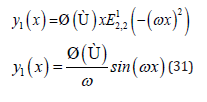
and we have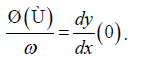 
Conclusion
As a general remark, we point out that it was possible to generalize the model of to include the anomalous diffusion ingredients [19-22]. The generalization was carried out with the aid of the Fractional Calculus and its usual techniques. We found a general solution in terms of three parameter Mittag-Leffler function and it was possible to demonstrate that the general solution yields the correct result obtained by for the non-anomalous case. Since membrane are widely used in many applications and naturally appears in biological systems, then we believe that this result can useful to many other researchers.
Acknowledgement
The authors thank the Foundation for Research Support of the State of Minas Gerais (FAPEMIG), through the term APQ-01366-16.
References
- Golubovic Z, Dragan PV, Zoran GD, Srdan TJ, Milan DM (2015) The Size-distribution of solid particles in a techni-cal water. 2nd International Symposium on Agricultural Engineering, Serbia.
- Tasic SJ, Golubovic ZZ, Petrovic DV, Golubovic Z (2009) On the applicability of morphometric method for evaluation of the waterborn particles size distribution, 26th Symposium on Advances in Experimental Mechanics, Austria.
- Kurt WT, Dragan VP, Zoran G, Natasa T (2012) Mathematical model for the particle size distribution of a kieselguhr lter granulation. Metalurgia International 17(10): 192-197.
- Kurt WT, Dragan VP, Rade RL, Zoran G, Vjekoslav T (2017) One-dimensional diffusion equation for the particle size distribution of perlite filter granulation. Technical Gazette 24(3): 943-948.
- Dragan VP, Rade RL, Kurt WT, Zorana G (2012) The uniformity of wheat seeding over an area and depth. 29th Danubia-Adria-Symposium on Advances in Experimental Mechanics, University of Bel-grade, Serbia.
- Dragan VP, Zoran DG, Zora D, Kurt WT, Rade RL (2012) Facta Universitatis, Series: Mechanical Engineering 10(1): 1-6.
- Kurt WT, Doru P, Dragan PV, Rade RL, Zorana G (2013) Modeling the lateral uniformity of wheat seeding, ISAE-2013, 2nd International Symposium on Agricultural Engineering, University of Belgrade-Zemun, Serbia, pp. 271-279.
- Seber, GAF, Wild CJ (2003) Nonlinear Regression. J Wiley and Sons, USA.
© 2018 Adélcio C Oliveira. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version