- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Evolutions in Mechanical Engineering
Determination of the Probability Size Distribution of Solid Particles in a Technical Water
Tomantschger Kurt W1*, Petrović Dragan V2 and Radojević Rade L2
1 Graz University of Technology, Institute of Analysis, Austria
2 University of Belgrade, Faculty of Agriculture, Institute for Agricultural Engineering, Belgrade-Zemun, Serbia
*Corresponding author:Tomantschger Kurt W, Graz University of Technology, Institute of Analysis and Number Theory, Steyrergasse 30, 8010 Graz, Austria
Submission: September 11, 2018;Published: October 16, 2018
ISSN: 2640-9690Volume1 Issue4
Abstract
Measuring the size distribution of solid contaminants born by the technical cooling water has an important role. Therefore, in this paper a partial differential equation which describes the probability size distribution of solid contaminants born by technical cooling water is presented and solved. It is demonstrated that the differential equation possesses an analytical solution in the form of the Gibbs-Boltzmann distribution function. The fitting function of probability density function represents a solution of the partial differential equation.
Before evaluation, the sampled water was prepared with filtration equipment. Extracing particles are digitized under scanning microscope. Finally, the particle sizes of contaminants are measured by digital image analysis technique, incorporated in a special program.
Keywords:Partial differential equation; Waterborn contaminants; Particle size distribution; Probability density function
Introduction
Heat, which can be used no more, is dissipated in many factories. Since water has a high heat absorption capacity, the heat transport is usually carried out by means of cooling water. This technical water is found not only in cooling systems, but also in radiators, etc. Particles of different sizes appear in such liquids. They also occur in gases, such as air pollution. So not only the experiments [1,2] but also the mathematical modeling [3-5] of different processes in technology and agriculture had been strongly intensived during the last time. An example of these many processes is the counting of particles suspersed in a liquid or gaseous medium.
In this paper a diffusion equation which describes the waterborn solid contaminants size distribution in a technical cooling water is solved. The solutions are experimentally verified in [1,2].
Diffusion Equation
y = y(x, t) denotes the probability size distribution of waterborn solid contaminants with the particle diameter x and the time t, t > 0. Then the differential equation which describes this diffusion process takes the form
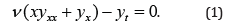
ν is a known positive constant and represents the drift velocity. For getting an idea of how the solution of this diffusion equation might look like, equation (1) is simplified. Writing the factor of in ν the form (xyx)x and replacing x by a constant k, (1) becomes
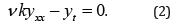
This is the simplest diffusion equation and possesses the solution
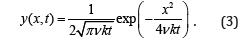
Since the coefficients of a differential equation also determine the solution, in (1) this is x, and because (2) is also a parabolic equation as (1), it can be assumed that the solution of (1) also is of the form (3). t exists in (1) and (2) only as a derivative. Therefore, it is obvious that t also appears in the solution of (1) as powers, as in (2). So, a solution of the form
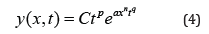
is supposed. C represents an arbitrary constant. The constants a, n, p and q are unknown real numbers. a=0, n=0 and q=0 are excluded. Inserting (4) into the diffusion equation (1) yields the conditional equation
for the four unknown constants. Since x and t are independent variables, the coefficients of each power of x and t vanish. Equation (5) contains four powers of x as well of t. Starting with the comparison of powers of x it is assumed that at least two powers of x in (5) are equal. This excludes trivial solutions. Thus, the following three cases are thereby left:
Case 1: n=-1
Now (5) has the form
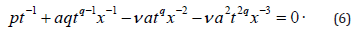
Equating the factor of x-1 or x-2 or x-3 to zero yields a=0, which is useless.
Case 2: n =1/2
In this case (5) is
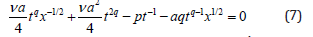
As in Case 1 the factors of x-1/2 and x1/2 yield y=y(t).
Case 3: n = 1
Here (5) becomes
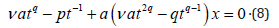
Therefore, the coefficient comparisation with respect to x provides
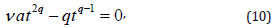
Taking q=-1 from (9) implies p=aν . Substituting q=-1 in (10) the comparison of powers with respect to t yields aν =-1. This gives a= -v-1 and p=-1. So the solution (4) of the partial differential equation (1) is
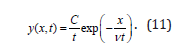
The Normalization Condition
Making use of the normalization condition
and substituting the solution (11) into this integral yield
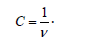
Thus, the final solution
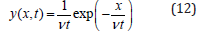
of the diffusion equation is calculated. The papers [1,2] contain the results of the corresponding experiments in which sizes had been measured with a microscopic morphometric method.
Experimental Results
This chapter lists some important results, which are given in [1]. The solid contaminants, suspended in a technical water was used in Tigar Tire company-Pirot, Serbia [6-8]. On the base of experimental data, the empirical probability density function of particle sizes is established using non-linear data fitting by using the iterative algorithm of Levenberg-Marquardt (9), according the exponential function. The peak value (around 600) of the probability density function arises at d=0.125mm (125μm). However, for d>0.75mm (755μm), its value decreases below 10. The smallest evident particle had equivalent diameter of only 0.036mm (36μm). Fitting the probability density function of the equivalent diameter d of solid contaminants, suspended in a technical water, had given
y0 = constant. This function represents a solution (12) with t = 1.
Remark: Formula (13) represents a Boltzmann distribution resp. Gibbs-Boltzmann distribution.
Conclusion
General purpose of mathematical modeling of the processes and operations in modern agriculture is well known and recognized worldwide. Following the common practice, in the present paper is presented a partial differential equation model describing the lateral probability density function of solid particles in a technical water. The basic goal of approximating an experimentally determined probability density function with an analytic function having appropriate shape is to describe a large amount of empirical data, which are represented by empirical statistical distribution.
References
- Golubović ZZ, Petrović DV, Golubović ZD, Tasiić SJ, Milosavljević MD (2015) The Size-distribution of solid particles in a technical water. 2nd International Symposium on Agricultural Engineering, Serbia.
- Tasić SJ, Golubović ZZ, Petrović DV, Golubović ZD (2009) On the applicability of morphometric method for evaluation of the waterborn particles size distribution, 26th Symposium on Advances in Experimental Mechanics, Austria.
- Tomantschger KW, Petrović DV, Golubović Z, Trisović n (2012) Mathematical model for the particle size distribution of a kieselguhr filter granulation. Metalurgia International 17(10): 192- 197.
- Tomantschger KW, Petrović DV, Radojević RL, Golubović Z, Tadić V (2017) One-dimensional diffusion equation for the particle size distribution of perlite filter granulation. Technical Gazette 24(3): 943-948.
- Petrović DV, Radojević RL, Tomantschger KW, Golubović Z (2012) The uniformity of wheat seeding over an area and depth. 29th Danubia- Adria-Symposium on Advances in Experimental Mechanics, University of Bel-grade, Serbia.
- Dragan VP, Zoran DG, Zora D, Kurt WT, Radojević RL (2012) Facta Universitatis, Series: Mechanical Engineering 10(1): 1-6.
- Tomantschger KW, Paunescu D, Petrović DV, Radojević RL, Golubović Z (2013) Modeling the lateral uniformity of wheat seeding, ISAE-2013, 2nd International Symposium on Agricultural Engineering, University of Belgrade-Zemun, Serbia, pp. 271-279.
- Seber GAF, Wild CJ (2003) Nonlinear Regression. J Wiley and Sons, USA.
© 2018 Tomantschger Kurt W. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version