A SIZE- BIASED DISCRETE AKASH DISTRIBUTION WITH PROPERTIES AND ITS APPLICATIONS

Size-biased distributions are a case of weighted distributions which arise naturally in practice when observations from a sample are recorded with probability proportional to some measure of unit size. In field applications, size-biased distributions can arise either because individuals are sampled with unequal probability by design or because of unequal detection probability. Size-biased distributions come into play when organisms occur in groups, and group size influences the probability of detection. Fisher [1] firstly introduced these distributions to model ascertainment biases which were later reformulated by Rao [2] in a unifying theory for problems where the observations fall in non-experimental, nonreplicated and non-random categories. Size-biased distributions have applications in almost every fields of knowledge including environmental science, econometrics, social science, biomedical science, human demography, ecology, geology, forestry etc. Further, size-biasing occurs in many unexpected contexts such as statistical estimation, renewal theory, infinite divisibility of distributions and number theory. Van Duesen [3] has detailed study about the applications of size-biased distributions for fitting distributions of diameter at breast height (DBH) data arising from horizontal point sampling (HPS). Later, Lappi J et al. [4] have applied size-biased distributions to analyze HPS diameter increment data. The applications of sizebiased distributions to the analysis of data relating to human population and ecology can be found in Patil & Rao [5,6].

Let a random variable has probability distribution P0 ( x;θ ) ; x = 0,1, 2,...,θ > 0 . If sample units are weighted or selected with probability proportional to xα , then the corresponding size-biased distribution of order α is given by its probability mass function (pmf)

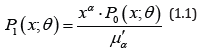
Where 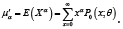The distribution is known as size-biased or area biased according as α =1 or α = 2 respectively.

Shanker [7] introduced one parameter Akash distribution defined by probability density function (pdf) and cumulative distribution function (cdf)

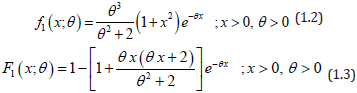
Shanker [7] has discussed its various interesting and important statistical properties, estimation of parameter and applications.

Berhane et al. [8] introduced a discrete-Akash distribution (DAD), discrete form of Akash distribution using infinite series approach of discretization having pmf

Various statistical properties of DAD, estimation of parameter and applications to model count data have been studied by Berhane [8] and it has been observed that it gives better fit than both Poisson distribution (PD) and Poisson-Lindley distribution (PLD), a Poisson mixture of Lindley [9] distribution and introduced by Sankaran [10]. The first four moments about origin and the variance of DAD obtained by Berhane et al. [8] are given by

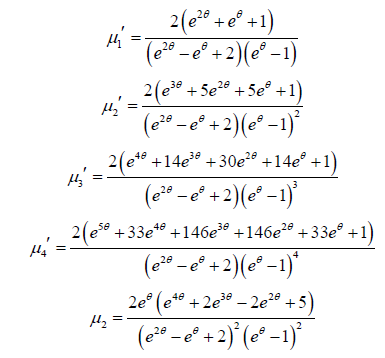
Simon et al. [11] introduced a size-biased discrete Lindley distribution (SBDLD) defined by its pmf

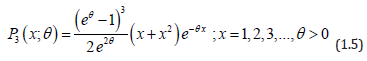
Statistical properties, estimation of parameter using both the method of moment and the method of maximum likelihood and the applications of SBDLD are available in Simon et al. [11] Note that a discrete Lindley distribution (DLD) using infinite series approach of discretization has been proposed by Berhane and Shanker [12] from Lindley distribution and its properties, estimation and applications are available in Shanker et al. [12].

It has been observed that DAD gives much closer fit over DLD, PLD and Poisson distribution, it is expected that size-biased discrete Akash distribution (SBDAD would also give much better fit over SBPD, SBPLD and SBDLD. Keeping these points in mind, SBDAD has been proposed by size-biasing the discrete-Akash distribution (DAD) of Berhane et al. [8], a discrete form of continuous Akash distribution introduced by Shanker [7]. Its moments and momentsbased measures including coefficient of variation, skewness, kurtosis and index of dispersion have been derived. The estimation of its parameter has been discussed using the method of moment and the method of maximum likelihood. Four examples of observed real datasets have been presented to test the goodness of fit of SBDAD over size-biased Poisson distribution (SBPD), size-biased Poisson-Lindley distribution (SBPLD), size-biased Poisson-Akash distribution (SBPAD) and size-biased discrete Lindley distribution (SBDLD).

Using (1.1) and (1.4) and the expression for the mean of DAD, the size-biased discrete-Akash distribution (SBDAD) with parameter θ can be defined by its pmf

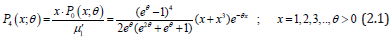
It can be easily verified that SBDAD is unimodal and have increasing failure rate. Since

is a deceasing function of x, P4(x;θ), is log-concave. Therefore, SBDAD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). The definitions and relationship between these aging concepts have been discussed in Barlow [13]. The graphs of the pmf of SBDAD (2.1) for varying values of the parameter (Figure 1).

The size-biased Poisson-Lindley distribution (SBPLD) introduced by Ghitany et al. [13] is defined by its pmf

Figure 1: Graphs of pmf of SBDAD for varying values of the parameter θ .

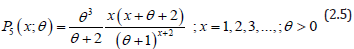
It should be noted that SBPLD is a size-biased version of Poisson-Lindley distribution (PLD) introduced by Sankaran [10]. Ghitany et al. [14] have discussed its various mathematical and statistical properties, estimation of the parameter using maximum likelihood estimation and the method of moments, and goodness of fit. Shanker et al. [15] has critical study on the applications of SBPLD for modeling data on thunderstorms and found that SBPLD is a better model for thunderstorms than size-biased Poisson distribution (SBPD). The size-biased Poisson-Akash distribution (SBPAD) proposed by Shanker [16] is defined by its pmf

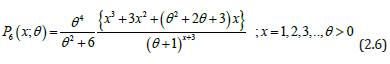
Note that SBPAD is a size-biased version of Poisson-Akash distribution (PAD) suggested by Shanker [17]. Shanker has detailed study on various statistical properties, estimation of parameter and applications of both PAD and SBPAD.

Using (2.1), the r th moment of origin 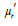of the SBDAD (2.1) can be obtained as

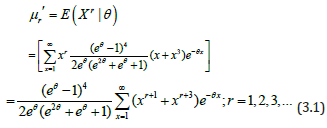
Taking in (3.1), the first four moments about origin of the SBDAD (2.1) are thus obtained as

Now, using the relationship between moments about mean and the moments about origin, the moments about mean of the SBDAD (2.1) can be obtained as

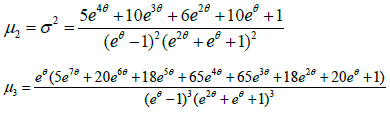
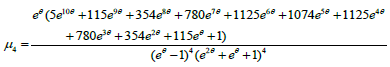
The coefficient of variation(C.V ), coefficient of Skewness , coefficient of Kurtosis (β2) and index of dispersion (γ ) of the SBDAD (2.1) are thus obtained as

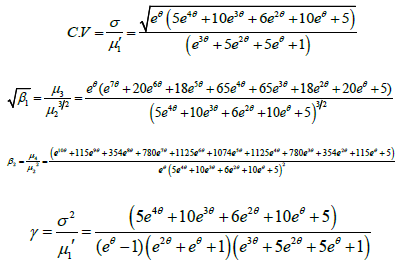
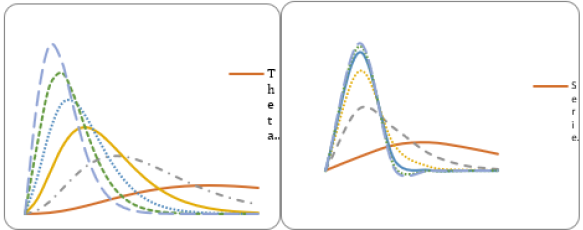
The graphs of coefficient of variation (C.V ), coefficient of Skewness , coefficient of Kurtosis (β2) and index of dispersion (γ ) of the SBDAD are shown in (Figure 2). It is obvious that C.V and index of dispersion are monotonically decreasing whereas coefficient of skewness and coefficient of kurtosis are monotonically increasing for increasing values of the parameter θ.

Figure 2: Graphs of C.V, coefficient of Skewness, coefficient of Kurtosis and index of dispersion of the SBDAD for varying values of the parameter θ .

It can be easily verified that SBDAD is over-dispersed (μ <σ 2 ), equi-dispersed (μ =σ 2 ) and under-dispersed for θ <(=)>θ ∗ = 0.583686 . It should be noted that SBDLD is over-dispersed (μ <σ 2 ), equidispersed (μ =σ 2 )and under-dispersed for θ <(=)>θ ∗ =1.00505 .

Method of moment estimate (MOME): Equating the population mean to the corresponding sample mean, the method of moment estimate (MOME) 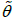of θ of SBDAD is the solution of the following non-linear equation in θ

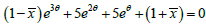, where is the sample mean.

Maximum likelihood estimate (MLE): Let x1, x2,...,xn be a random sample of size from the SBDAD (2.1) and let fx be the observed frequency in the sample corresponding to X = x (x =1, 2,3,..., k) such that 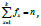where is the largest observed value having non-zero frequency. The likelihood function L of the SBDAD (2.1) is given by

The log likelihood function can be obtained as

The first derivative of the log likelihood function is thus given by

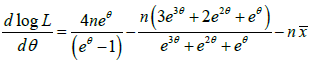
where 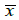is the sample mean

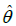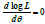The maximum likelihood estimate (MLE), of θ of SBDAD (2.1) is the solution of the equation and is given by the solution of the following non-linear equation

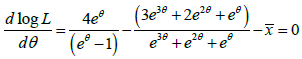
This gives 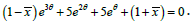Thus, both the method of moment and the method of maximum likelihood gives the same equation for estimating the parameter θ . This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula-Falsi method etc. In the present paper, Newton-Raphson method has been used.

As we know that size-biased distributions are used to model data when organism occur in groups and the size of the group influence the probability of detection. Here we considered four datasets relating to size-distribution of freely forming small groups at various public places, available in Coleman et al. [18]. The goodness of fit of SBPD, SBPLD, SBPAD, SBDLD and SBDAD has been presented for four count datasets (Table 1-3).

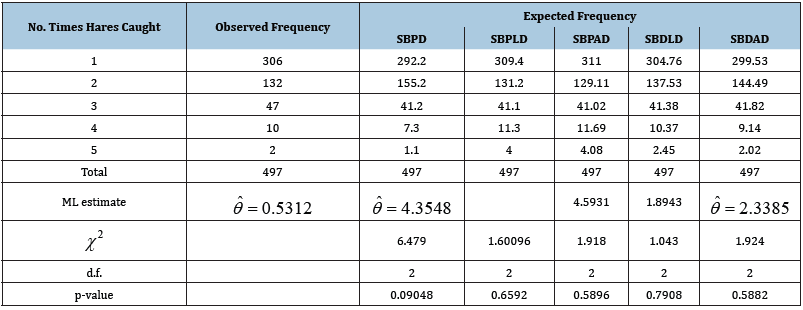
Table 1: Pedestrians-Eugene, Spring, Morning.

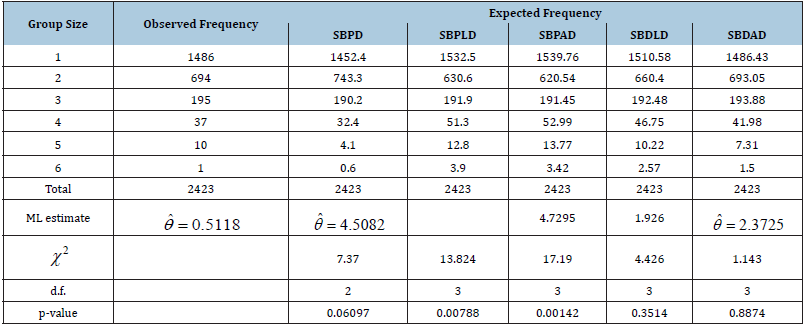
Table 2: Shopping Groups-Eugene, Spring, Department store and Public Market.

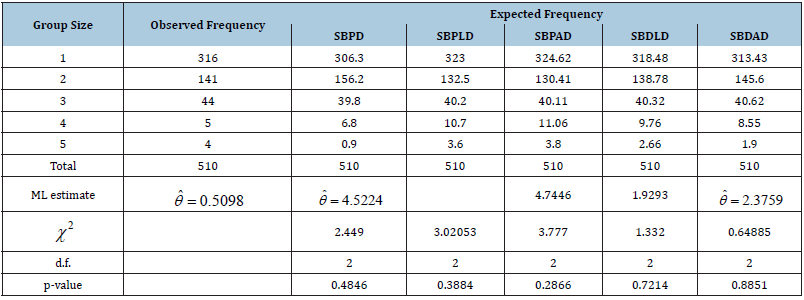
Table 3: Play Groups-Eugene, Spring, Public Playground D.

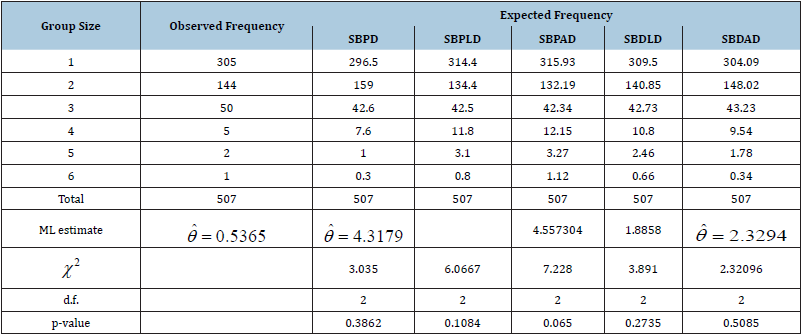
It is obvious from the goodness of fit in these tables that SBDAD gives much closer fit than other size-biased distribution except in (Table 4), where SBDLD gives better fit over other size-biased distributions. Therefore, SBDAD can be considered as a model for size-distribution of freely forming small groups.

Table 4: Play Groups-Eugene, Spring, Public Playground A.

In the present paper size-biased Discrete-Akash distribution (SBPAD), a simple size-biased version of the discrete-Akash distribution (DAD) of Berhane et al. [8] has been proposed and studied. Its raw moments and central moments have been obtained and hence expressions for coefficient of variation (C.V.), skewness, kurtosis and index of dispersion have been presented and their natures have been discussed graphically. The estimation of its parameter has been discussed using the method of moments and the method of maximum likelihood estimation. The goodness of fit of the SBDAD has been discussed with four examples of observed real datasets over SBPD, SBPLD, SBPAD, SBDLD and it is observed that SBDAD gives much closer fit. Therefore, SBDAD can be considered an important distribution for modeling distribution of freely forming group size.

1. Fisher RA (1934) The effects of methods of ascertainment upon the estimation of frequencies. Ann Eugenics 6(1): 13-25.
2. Rao CR (1965) On discrete distributions arising out of methods of ascertainment. in: Patil. GP (eds) Classical and Contagious Discrete Distributions. Statistical Publishing Society Calcutta, India, pp. 320-332.
3. Van Deusen PC (1986) Fitting assumed distributions to horizontal point sample diameters. For Sci 32(1): 146-148.
4. Lappi J, Bailey RL (1987) Estimation of diameter increment function or other tree relations using angle-count samples. Forest Science 33(3): 725-739.
5. Patil GP, Rao CR (1977) The weighted distributions: A survey and their applications. In: Applications of Statistics, Krishnaiah PR (Ed.), North Holland Publications Co., Amsterdam, Netherlands, pp. 383-405.
6. Patil GP, Rao CR (1978) Weighted distributions and size-biased sampling with applications to wild-life populations and human families. Biometrics 34(2): 179-189.
7. Shanker R (2015) Akash distribution and its applications. International Journal of Probability and Statistics 4(3): 65-75.
8. Berhane A, Shanker R (2018 a) A discrete Akash distribution with applications. Turkey Journal of Biostatistics 10(1): 1-12.
9. Lindley DV (1958) Fiducial distributions and Bayes theorem. Journal of the Royal Statistical Society 20(1): 102-107.
10. Sankaran M (1970) The discrete Poisson-Lindley distribution. Biometrics 26(1): 145-149.
11. Simon S, Shanker R (2018) Size-biased discrete Lindley distribution and its applications to model distribution of freely forming small group size. Biometrics & Biostatistics International Journal 7(2): 96-101.
12. Berhane A, Shanker R (2018b) A discrete Lindley distribution with application in biological sciences. Biometrics & Biostatistics International Journal 7(1): 1-5.
13. Barlow RE, Proschan F (1981) Statistical theory of reliability and life testing: probability models. Silver Spring, USA.
14. Ghitany ME, Al Mutairi DK (2008) Size-biased Poisson-Lindley distribution and its applications. METRON-International Journal of Statistics LXVI (3): 299-311.
15. Shanker R, Hagos F, Abrehe Y (2015) On size-biased Poisson-Lindley distribution and its applications to model thunderstorms. American Journal of Mathematics and Statistics 5(6): 354-360.
16. Shanker R (2017b) Size-biased poisson-Akash distribution and its applications. International Journal of Statistics and Applications 7(6): 289-297.
17. Shanker R (2017a) The discrete poisson-Akash distribution. International Journal of probability and Statistics 6(1): 1-10.
18. Coleman JS, James J (1961) The equilibrium size distribution of freely forming groups. Sociometry 24(1): 36-45.