- Submissions

Full Text
COJ Technical & Scientific Research
Mappings on Fuzzy Soft Topological Spaces
Jingshui Ping*
School of Finance and Mathematics, China
*Corresponding author: Jingshui Ping, School of Finance and mathematics, Huainan, China
Submission: September 20, 2019; Published: September 30, 2019

Volume2 Issue3September, 2019
Abstract
This paper had been popularized the operational property of fuzzy soft mapping on the basis of fuzzy soft mapping. We had set up a kind of soft mapping and fuzzy soft continuous on fuzzy soft topology and discussed the application of fuzzy soft mapping and its composite properties on the construction of fuzzy soft topology.
Keywords: Fuzzy soft set; Fuzzy soft mapping; Fuzzy soft topology; Fuzzy soft continuous
Introduction
Molodtsov put forward the soft set theory in order to handling uncertain problems in 1999. This theory had overcome a main shortcoming of mathematical methods; that was lacking parameter tool. The soft set theory has been successfully applied in several fields such as decision analysis, pattern recognition and data collection. Maji [1] perfected the theoretical system of soft set and studied the fuzzy soft set theory. Paper included the research of the algebraic structure of soft set; and Hazra [2] had set up the soft topology construction. In Kharal & Ahmad [3] began to study fuzzy soft mapping. In 2011, Bekir T & Burc K [4] set up a fuzzy soft topology structure. In 2012, Abdülkadir [5] studied some properties of soft mapping on soft topology. Based on all these mentioned above, we research on fuzzy soft mapping on fuzzy soft topology and its application in fuzzy soft topology structure [6].
Problem Statement and Preliminaries
Definition 1
[7] Let A ⊂ E and F(U)be the set of all fuzzy sets in U. Then the pair ( f , A) is called a fuzzy soft set over U , where f : A→ F(U) is a function. A fuzzy soft set ( f , A) can be viewed [2] (f,A) = {a = {ufa(u)|u∈ U} [8-12].
Definition 2
13] Let g~ = (h, p) , where h :U →U′ and p : E → E′ be mappings. Let ( f , A) and (k,C) be fuzzy soft sets, over U and U′ , where A ⊂ E andC ⊂ E′
A fuzzy soft image of a fuzzy soft set ( f , A) under mapping g~ is defined as follows:

A fuzzy soft inverse image of a fuzzy soft set (k,C) under mapping g is defined as
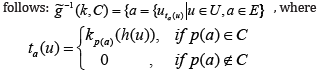
Remark 1: The definition mentioned above, actually, is a kind of improvement of 3.2 definition in document [13].
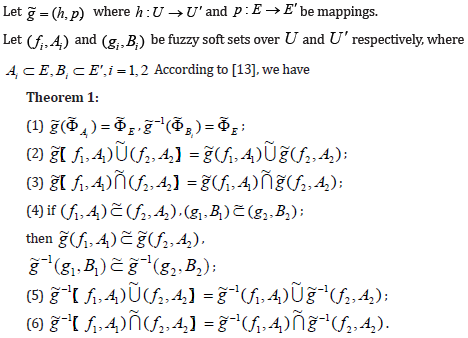
Mappings on Fuzzy Soft Topological Spaces
Definition 3
[14] Let (γ , X ) be an element of F(U;E) , P(γ , X ) be the set of all fuzzy soft subsets of ) , ( X γ and τ ~ be a subfamily of P(γ , X ) .Then τ ~ is called fuzzy soft topology on (γ , X ) if the following conditions are satisfied:
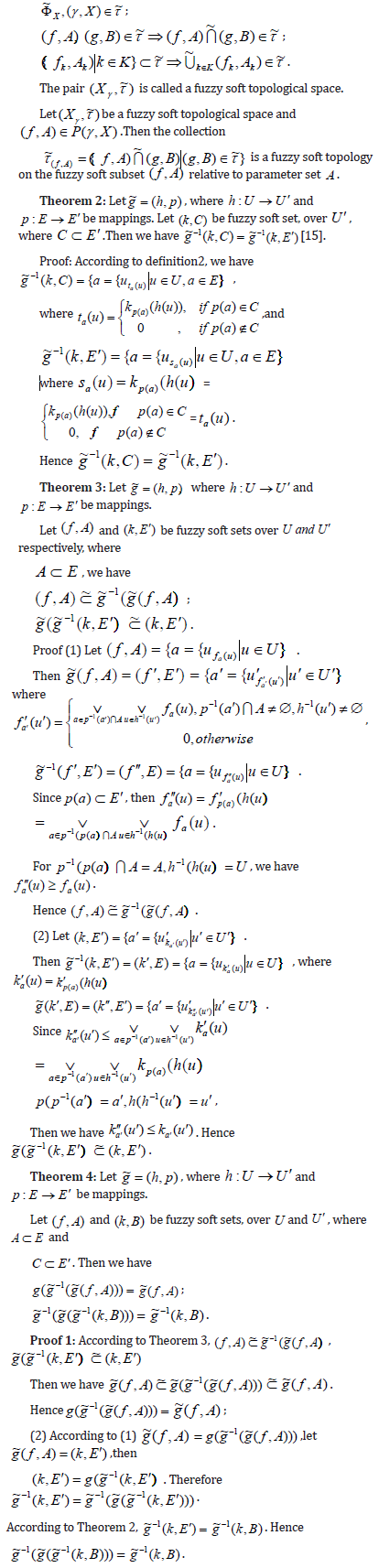
Definition 4


Conclusion
Fuzzy soft mapping is an extremely significant part in studying the spacious property of fuzzy soft topology. This paper popularizes fuzzy soft mapping as well as the operational properties of its inverse and composite operation. We set up the fuzzy soft continuous on fuzzy soft topology and study the application of fuzzy soft mapping’s various properties in the construction of fuzzy soft topology. As for the question that how to establish fuzzy soft quotient topology space by fuzzy soft mapping, detailed information will be given in author’s another paper.
References
- Maji PK, Roy AR, Biswas R (2002) An application of soft sets in a decision-making problem. Computers and Mathematics with Application 44(8-9): 1077-1083.
- Hazra H, Majumdar P, Samanta SK (2012) Soft topology. Fuzzy Inf Eng 4(1): 105-115.
- Kharal A, Ahmad B (2009) Mappings on fuzzy soft classes. Advances in Fuzzy Systems 2009: 6.
- Tanay B, Kandemir BM (2011) Topological structure of fuzzy soft sets. Computers & Mathematics with Applications 61(10): 2952-2957.
- Aygunoglu A, Aygun H (2009) Introduction to fuzzy soft groups. Computers & Mathematics with Applications 58(6): 1279-1286.
- Molodtsov D (1999) Soft set theory-first results. Computers and Mathematics with Applications 37(4-5): 19-31.
- Cagman N, Enginoglu S (2010) Soft set theory and uni-int decision-making. European Journal of Operational Research 207(2): 848-855.
- Cagman N, Enginoglu S (2010) Soft matrix theory and its decision making. Computers and Mathematics with Application 59(10): 3308-3314.
- Zou Y, Xiao Z (2008) Data analysis approaches of soft sets under incomplete information. Know Based Syst 21(8): 941-945.
- Maji PK, Biswas R, Roy AR (2003) Soft set theory. Computers and Mathematics with Applications 45(4-5): 555-562.
- Maji PK, Biswas R, Roy AR (2001) Fuzzy soft sets. The Journal of Fuzzy Mathematics 9(3): 677-692.
- Aktas H, Cagman N (2007) Soft sets and soft groups. Information Sciences 177(13): 2726-2735.
- Feng F, Young BJ, Xian Z (2008) Soft semirings. Computers and Mathematics with Application 56(10): 2612-2628.
- Jun YB, Park CH (2008) Applications of soft sets in ideal theory of BCK/BCI-algebras. Information Sciences 178(11): 2466-2475.
- Aygünoğlu A, Aygün H (2012) Some notes on soft topological spaces. Neural Comput & Applic 21(Suppl 1): 113-119.
© 2019 Jingshui Ping. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






