- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
COJ Technical & Scientific Research
A Pure Mathematical Proof of the Four Color Problem
Fayez Fok Al Adeh*
President of the Syrian Cosmological Society, Syria
*Corresponding author: Fayez Fok Al Adeh, President of the Syrian Cosmological Society, Damascus, Syria
Submission: June 26, 2018;Published: July 05, 2018
Volume1 Issue1 July 2018
Abstract
As stated originally the four-color problem asked whether it is always possible to color the regions of a plane map with four colors such that regions which share a common boundary (and not just a point) receive different colors. In the long and arduous history of attacks to prove the four colortheorem many attempts came close, but what finally succeeded in the Apple-Haken proof of 1976 and also in the recent proof of Robertson, Sanders, Seymour and Thomas 1997 was a combination of some old ideas and the calculating powers of modern-day computers. Thirty years after the original proof, the situation is still basically the same,no pure mathematical proof is in sight.Now I give in my paper such a pure mathematical proof
Introduction
The four color problem asks whether it is always possible to color the regions of a plane map with four colors such that regions which share a common boundary (and not just a point) receive different colors. Coloring the regions of a plane map is really the same task as coloring the vertices of a plane graph. We place a vertex in the interior of each region (including the outer region) and connect two such vertices belonging to neighbouring regions by an edge through the common boundary. The resulting graph G, the dual graph of the map M, is then a plane graph, and coloring the vertices of G in the usual sense is the same as coloring the regions of M. Because of this construction we may as well concentrate on vertex-coloring graphs drawn on the 2-sphere S2 and will do so from now on. Note that we may assume that G has no loops or multiple edges, since these are irrelevant for coloring [1]. First note that adding edges can only increase the chromatic number. In other words, when H is a subgroup of G, then X1 (H) ≤ X1 certainly holds. χ1 is the list chromatic number, hence we may assume that G is connected.
Since ordinary coloring is just the special case of list coloring, we obtain for any graph G
A. χ(G) ≤ χ1(G)
where χ (G) is the ordinary chromatic number. Now we consider the given map M (including the outer region) and its’ dual graph G (including the vertex in the interior of the outer region) the regions of M exhaust all of S2. Thus S2 is SO3-paradoxical using the regions of the map M some of the employed elements of SO3 may coincide with the identity of SO3). Now we color the vertices of the dual graph G in such a way that the two vertices at the two ends of any edge of the graph G receive different colors, and such that the number of colors used is a minimum. Let n be the minimum number of different colors used. For each color i (i=1,2,… …,n ) we collect all the regions of the map M with the property that the vertices of G in the interiors of all of these regions have the same color i. Let Ai be the union of the collection of all such regions.
figure 1:
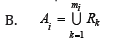
Where Rk (K=1,2,…,mi) are the regions of the map M with the property that the vertices of G in the interiors of all these regions have the same color i [2]. mi the number of these regions Rk (K=1,2,…,mi). For any f∈SO3 acting on S2, and for any function f in general, we have
figure 2:
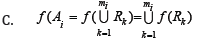
This means that S2 is SO3-paradoxical using the new subsets Ai(i=1,2,….,n). We call these subsets Ai (i=1,2,….,n ). The derived subsets based on minimum coloring of a given map M.
We can then obtain immediately the following easy theorem:
D. Theorem: S2 is SO3-paradoxical using the derived subsets Ai(i=1,2,….,n). The number of these subsets n equals the minimum number of colors used.
We mention now the following known theorem:
E. Theorem: S2 is SO3-paradoxical using four regions, and the four cannot be improved.
What about the greatest lower bound of all the possible minimum numbers of colors used in all possible cases?
According to this last theorem (E) and in reference to theorem (D) above ,we assert that whenever an SO3-paradoxical decomposition of S2 is given using derived subsets in the sense of theorem (D) above [3], the greatest lower bound of all possible numbers of these subsets is four, and the four cannot be improved. Therefore, according to theorem (D) above, the greatest lower bound of all minimum numbers of colors used to color any graph (or map) is four, and the four cannot be improved. This concludes the proof of the four color conjecture.
References
- Aigner M, Ziegler GM (2002) Proofs from the Book. Springer Verlag, Berlin, Germany.
- Wagon S (1994) The banach-tarski paradox. Cambridge University Press, (2nd edn), New York, USA.
- Saaty TL, Kainen PC (1977) The four color problem. Mcgraw-Hill Book Company, New York, USA.
© 2018 Fayez Fok Al Adeh. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version