Artificial Intelligence Algorithm for Path Planning Optimization in Planar Mechanisms

Mechanical mechanisms are the foundation of modern machinery providing the framework through which theoretical principles of mechanics are transformed into practical applications. They are designed to transform input energy into precisely controlled movement of mechanical parts. The evolution of kinematic design, actuators, motors and the control methodologies of mechanisms led to the appearance of modern robotics [1]. The mechanism can be classified in two main categories the planar and spatial mechanisms. Their distinguished performance is based on the relative motion of their rigid bodies [2,3]. The motion of the bodies of planar mechanisms takes place in the same or parallel planes. If their relative motion is performed in a different plane, the mechanism is characterized as spatial [4]. As a result, the movement of the end effectors of planar mechanisms is performed in the 2D space while in spatial mechanisms it is executed in 3D. The kinematic analysis of a mechanism determines its operational behavior. Kinematic analysis examines the motion of the mechanism’s components by analyzing the effect of their position, velocity, and acceleration. The area where the mechanism’s end effector can move without encountering any constraints from its mechanical configuration is called the mechanism’s workspace [5]. The mechanism’s workspace is crucial for securing the feasibility of the desired motions, the trajectory designing and the application field of the mechanism. Path planning algorithms try to find the shortest collision free path that can connect a starting to an ending point region. In the application of path planning algorithms to mechanisms, it is necessary for the generated path to comply with mechanisms capabilities. As a result, the path generation of a planar mechanism requires 2D path planning. Researchers have proposed several algorithms for generating 2D paths [6-9], 3D [10-12] and 4D [13-16]. Path planning algorithms generate a series of coordinates within the workspace of the mechanisms. The procedure of approaching these coordinates from the mechanism’s end effector is by the kinematic model of every mechanism. In industrial robotic arms with 6 degrees of freedom is determined by the Denavit-Hartenberg (DH) notation [17]. The numerical values of the joint angles for approaching the desired coordinates are determined by solving the inverse kinematics problem [18,19].

The grid method is utilized for simulating virtually the real world and solving the path planning problem. The grid method consists of many elementary units with the same dimensions. Each elementary unit is represented by a discrete point in its center. The discrete point can be considered as free or as an obstacle. The free discrete point permits the robot to move on it, whereas the obstacle prohibits its movement in this region. By prohibiting movement, the obstacles encountered within the mechanism’s operating space are digitally simulated. The procedure of path finding is performed within the grid environment; as a result, the inaccurate representation of the real world in the grid environment can lead to paths that cannot be applied to the real-world conditions. The grid environment can represent a section of the workspace or embrace some regions that are not contained in the workspace. The Artificial Fish Swarm Algorithm (AFSA) described in [20] was utilized for solving the 2D path planning. The methodology of multiple laser activation described in [21] was also integrated into the algorithm. The methodologies of simple and advanced elimination, heatmap creation, heatmap random activation and the objective functions were used as described in [20].

The presented AFSA utilizes an expanded navigation model for the artificial fish in the grid environment. Specifically, the 24 possible movement points model is employed. The navigation model determines the set of possible movement points that the artificial fish can move from its current position during the process of the next point selection. The majority of path-planning algorithms in grid environments utilize the 8 possible movement point navigation model. The 24 possible movement point model enables transitions to 24 different positions and 16 directions, while the 8 possible movement point model permits movement to 8 positions along 8 directions. The additional directions provided by the 24 possible movement point model possible movement point model. The incorporation of the multiple laser activation method into the presented AFSA mitigates a fundamental limitation of standard AFSAs, namely the absence of a memory mechanism. The absence of a memory mechanism in the path-planning process hinders the identification of the optimal path, as it prevents the correction of errors within the generated path.

Figure 1:(a) General configuration experimental set up, (b)-(d) Robot position during path implementation (e) Resulting path using AFSA, (f) Resulting path using ACO [11].

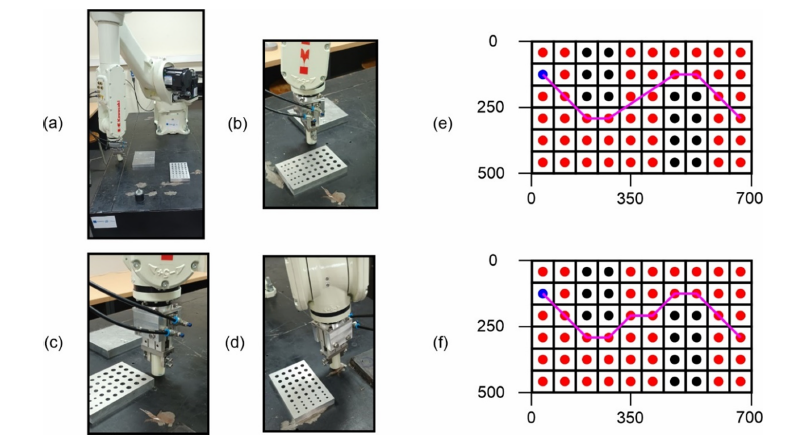
The 2D algorithm was employed for creating paths without collision for an industrial robotic arm with 6 degrees of freedom. The robotic arm operated only in 2 dimensions, its capability to move to the third dimension remained unexploited for experimental purposes. The planar motion of the robot’s end effector is executed within the X-Y plane, while the Z-coordinate is maintained at a constant, predetermined value. Furthermore, the orientation of the robot’s end effector is maintained unchanged throughout the operation. The inverse kinematics of the six-degree-of-freedom industrial robotic arm are determined in accordance with the methodology described in [22]. The Kawasaki RS010N industrial robotic arm was utilized for experiments. The parameter set is the same as [20]. Figure 1a shows the configuration where the experiments are conducted. Figure 1b-1d show the position of the robots end effector during the path prosecution. Figure 1e shows the optimal path created by the algorithm. The grid environment contains 60 discrete points. The environment’s density is considered as thin. The shape of the contained obstacles is rectangular and can be perfectly simulated from the grid’s elementary units. A thin grid environment simulates the workspace less accurately than a dense one because of the larger size of the elementary units. An advantage of a thin environment is the reduced computational requirements relative to the dense environments. In the examined case the utilization of a thin grid does not affect the quality of the solution because the shape and dimension of the obstacles do not lead to their oversized representation, resulting in savings in computational resources.

Figure 1f depicts the resulting path using the Ant Colony Optimization (ACO) method in [11]. The path length obtained using the AFSA algorithm is 843.42mm, whereas the path length derived from the ACO algorithm is 862.99mm. The path length generated by AFSA is 2.26% shorter compared to that obtained using ACO. The principal difference between the two methods is that the AFSA produced a path containing 6 nodes, whereas the ACO developed a path consisting of 10 nodes, indicating that AFSA generated a path comprising 40% fewer nodes. The computation time required by AFSA was 9,5 seconds, whereas ACO required 34,6 seconds (Figure 1).

The effective navigation of the end effector of planar mechanisms is vital in performing complex operations. The AFSA successfully found the shortest collision free path in a 2D environment with obstacles. The generated 2D path was applied in a real-world experiment and performed from an industrial robotic arm. The successful performance of the created path from a mechanism with complex kinematics such as the robotic arms indicates that the path can also be used for trajectory optimization cases in planar mechanisms. The created path specifies the coordinates within the mechanism’s workspace; however, the trajectory design depends on the kinematic model of the implemented mechanism. In cases where obstacles can be accurately represented by the elementary units of the grid environment, the thin density of the environment leads to qualitative solutions with low computational cost. The geometry and dimensions of obstacles are critical factors in establishing the appropriate grid resolution for path planning. Specifically, larger or more complexly shaped obstacles may require a denser grid to accurately capture their boundaries and avoid collisions. Obstacles that incorporate curved surfaces or irregular contours necessitate a higher grid resolution to ensure accurate representation within the environment. The choice of grid density directly impacts both the precision of the path and the computational resources required. A carefully balanced grid resolution ensures that the environment is modeled accurately enough to generate feasible paths while maintaining computational efficiency, particularly in scenarios involving intricate obstacle configurations or tight navigation constraints. The proposed technique may be adapted for more intricate environments, in both two-dimensional and threedimensional contexts, as well as for dynamic circumstances. In a 3D context, the algorithm would need to include vertical movement and avoid obstacles of varying heights and volumes. In dynamic environments, where obstacles may shift or the surroundings may evolve over time, the planner must incorporate real-time sensing and predictive mechanisms to enable on-the-fly path adaptation. These enhancements would enable the method to handle more elaborated scenarios commonly encountered in areas such as industrial automation, autonomous navigation, and aerial robotics.

1. Ceccarelli M (2023) Historical backgrounds on robot mechanism design. Robot Design, Mechanisms and Machine Science, Springer, UK, 123: 3-21.
2. Norton RL (2000) Design of machinery: An introduction to the synthesis and analysis of mechanisms and machines. (2^nd edn), McGraw Hill, USA, p. 924.
3. Unde J, Ito Y, Colan J, Hasegawa Y (2025) Kinematic analysis and experimental verification of transforming planar linkage mechanism. Robomech Journal 12: 1-16.
4. Zhang Y, Finger S, Behrens S (2025) More on machines and mechanisms. Rapid Design Through Virtual and Physical Prototyping, Carnegie Mellon University, USA.
5. Zhao J, Feng Z, Chu F, Ma N (2014) Workspace of the end effector of a robot mechanism. Advanced Theory of Constraint and Motion Analysis for Robot Mechanisms, Academic Press, Massachusetts, USA, pp. 159-200.
6. Lai YK, Vadakkepat P, Xiang C (2024) R2: Optimal vector-based and any-angle 2D path planning with non-convex obstacles. Robotics and Autonomous Systems 172: 104606.
7. Lin M, Yuan K, Shi C, Wang Y (2017) Path planning of mobile robot based on improved A* Proceedings of the 29^th Chinese Control and Decision Conference (CCDC), Chongqing, China, pp. 3570-3576.
8. Tao B, Kim JH (2024) Mobile robot path planning based on bi-population particle swarm optimization with random perturbation strategy. Journal of King Saud University-Computer and Information Sciences 36(2): 101974.
9. Zheng L, Yu W, Li G, Qin G, Luo Y (2023) Particle swarm algorithm path-planning method for mobile robots based on artificial potential fields. Sensors 23(13): 6082.
10. Han J (2019) An efficient approach to 3D path planning. Information Sciences 478: 318-330.
11. Mansour G, Chouridis I, Tsagaris A (2024) Finding the optimal path in a 3D environment with predefined obstacles. International Journal of Advanced Mechatronic Systems 11(1): 50-62.
12. Tu B, Wang F, Han X, Fu X (2024) Q-learning guided grey wolf optimizer for UAV 3D path planning. International Journal of Advanced Computer Science and Applications 15(7): 469-478.
13. Liu Y, Zhang X, Zhang Y, Guan X (2019) Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach. Chinese Journal of Aeronautics 32(6): 1504-1519.
14. Chouridis I, Mansour G, Papageorgiou V, Mansour MT, Tsagaris A (2025) Four-dimensional path planning methodology for collaborative robots’ application in industry 5.0. Robotics 14(4): 48.
15. Zhou J, Zhang H, Xue Q, Li Y (2025) Real-time 4D trajectory planning method for civil aircraft with high security in congested, stochastic, and dynamic airspace environment. Expert Systems with Applications 260: 125347.
16. Pollini L, Chouridis I, Mansour G, Chouridis A, Papageorgiou V, et al. (2025) Digital twin driven four-dimensional path planning of collaborative robots for assembly tasks in industry 5.0. Robotics 14(7): 97.
17. Nicolescu A, Ilie FM, Tudor George A (2015) Forward and inverse kinematics study of industrial robots taking into account constructive and functional parameter’s modeling. Proceedings in Manufacturing Systems 10: 157.
18. Atique, MMU, Ahad MAR (2014) Inverse kinematics solution for a 3DOF robotic structure using denavit-hartenberg convention. 2014 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh.
19. Lu C, Denavit-Hartenberg (D-H) Convention, p. 11.
20. Chouridis I, Mansour G, Tsagaris A (2024) Three-dimensional path planning optimization for length reduction of optimal path applied to robotic systems. Robotics 13(12): 178.
21. Chouridis I, Mansour G, Papageorgiou V, Mansour MT, Tsagaris A (2025) Enhanced hybrid artificial fish swarm algorithm for three-dimensional path planning applied to robotic systems. Robotics 14(3): 32.
22. Dikmenli S (2022) Forward & inverse kinematics solution of 6-DOF robots those have offset & spherical wrists. Eurasian Journal of Science Engineering and Technology 3(1): 14-28.