- Submissions

Full Text
COJ Robotics & Artificial Intelligence
From Robot to Universal Robotics
Vasilyev NS*
Department of Fundamental Sciences, Bauman Moscow State Technical University, Russia
*Corresponding author: Vasilyev NS, Department of Fundamental Sciences, Bauman Moscow State Technical University, Russia
Submission: February 28, 2025;Published: June 24, 2025

ISSN:2832-4463 Volume4 Issue4
Abstract
System-Informational Culture (SIC) ergonomics is based on Artificial Intelligence (AI) applications. The latter becomes the decisive factor of innovations. Robotics is developing in the direction of universality which can be accomplished in the paradigm of cooperative approach. Robots’ system can make decisions autonomously dis-tributing control over its behavior. Autonomous robotics emerges attracting achievements of AI. Robots are able to perform individual parts of the overall task together. They form a single Multiagent System (MAS) with intelligent actors pursuing their own objectives and interacting by messaging. The MAS is simulated as a relational cooperative game. Its formulation uses a variety of relationships. In order to jointly perform a universal task, robots have to solve effectively a scheduling problem. The optimal networking communications structure is built by them with the help of coalitions forming. The equilibrium scheduling can be obtained by means of polynomial distributive algorithm. Becoming of universal robotics takes place in the way.
Keywords:Multiagent system; Cooperative robotics; Intelligent agent; Scale of universal task; Scheduling; Monoidal category of binary relations; Preorder; Relational game; Equilibrium; Pareto effective solution; Communi-cations network
Introduction
An important role in the up-to-date SIC ergonomics plays robotics [1,2]. Robots’ team simulation needs to be made in the most general terms in order to provide universality of the discussed technology. A language of binary relations suits to the aims [3]. Robots are described by means of their preferences relations ρi,i∈I, given on the set of all tasks Α to be provided. They are operations to be made and robots’ locations in the working space. The overall task is ordered by means of a precedence relation .τ It means that all subtasks are to be completed according to the ordering (Α,τ). Allow the object (Α,τ) to be named the universal task. Robots are able to study their system configuration and make rational decisions [2]. Their awareness is based on messaging. They form an AI-powered multiagent system [4]. Agents themselves endeavor to choose the most suitable subtasks leaning on their preferences relations. The latter preorder the set Α in different ways. In particular, the smallest elements of the preordered set (Α,ρi) answer to requirements that cannot be at all accomplished by robots .i∈I It is supposed that every subtask Aj∈Α can be performed by any robot .iI∈ Agents may have heterogeneous capabilities. In the competition to choose tasks, those robots must win that can do the tasks better. For the purpose, robots are compared with the help of the given relationship 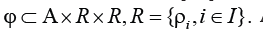 Artificial intelligence can be applied to the discussed MAS. It leads to some relational gaming problem solution [2,5,6]. Intelligent robots are players which apply acceptable strategies depending on their awareness. The classes of their strategies are defined according to the used information exchange [5].
Artificial intelligence can be applied to the discussed MAS. It leads to some relational gaming problem solution [2,5,6]. Intelligent robots are players which apply acceptable strategies depending on their awareness. The classes of their strategies are defined according to the used information exchange [5].
Earlier, the contributed simulation was carried out in case of more general game problems [6]. Now, it’s about relational cooperative game having a special kind. Anyway, robots’ system universality attainment is reduced to a scheduling problem solution [7]. It is grounded on the game principles of optimality [5]. The needed scheduling to be built must be stable and Pareto effective [8]. Based on the scheduling, robots’ team functioning is similar to the trading and load balancing control method applied to distributed systems [9-11].
Problem Formulation
So, there are intellectual players that have preferences relations
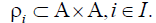 . The set Α does not include tasks impossible
to be executed. Relationship (Α, τ) graph defines time scale of the
universal task Α [6]. The agents are to select and complete the
subtasks
. The set Α does not include tasks impossible
to be executed. Relationship (Α, τ) graph defines time scale of the
universal task Α [6]. The agents are to select and complete the
subtasks  in the moments
in the moments 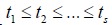 which obey the
ordering (Α, τ). Thus, robots i∈I will serve requirements in the
following sequences:
which obey the
ordering (Α, τ). Thus, robots i∈I will serve requirements in the
following sequences:
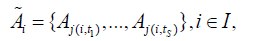
The scheduling must form a partition of the set Α:
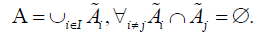
For the aims of the scheduling optimization, the relationships
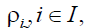 should be laid out from the set Α on the sequences set
should be laid out from the set Α on the sequences set
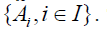 The continuations are denoted i ρ [3].
The continuations are denoted i ρ [3].
Robots’ specialization is to be also taken into account expressed with the help of 3-ary suitability relation ϕ. Its meaning is presented by its binary sections
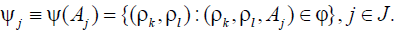
Robot l is more suitable and more effective to perform the
subtask Aj than his partner 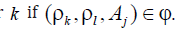 .
.
It is worth mentioning that all binary relations τ,ρi,ψj are preorders [3] known to all players.
Corresponding dynamic game is to be solved in which the players might maximize their continued preferences relations:
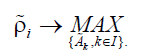
The agents’ goal is to find an optimal scheduling [7,9,11]. In the given case, this is understood as the game solution which is equilibrium and Pareto effective simultaneously [8]. The classes of acceptable strategies are defined by players themselves. They depend on the players’ awareness acquired through messaging [2, 4-6]. The needed equilibrium can be achieved due to communications exchange [5]. The players operate autonomously. Messaging ensures their cooperation. Mult objective optimization for scheduling in networked systems and decentralized control are contemporary manifestation of AI [9-11]. More detailed description of the corresponding relational dynamic game is given in the following section.
Cooperative Scheduling
Distributed decentralized control adds uncertainty to decision making. To diminish it, agents might coordinate their activity by messaging. Corresponding classes of strategies usage may guarantee existence of the game equilibrium solution [2,5,6].
The game communications network Γ building is also the result
of agents’ cooperation and part of agents’ strategies application. It
can be optimized autonomously by robots themselves [2]. In the
process, a set of robots’ coalitions Ck,k =1, 2,...,r emerges. Due
to it, players’ moves become partially ordered [3,5,6]. If a task
is chosen by an agent who informs some partners about it, the
latter make their decisions later than the former on the base of
the data. The coalitions are formed on the basis of consistency of
agents’ interests and suitability relation. Coalitions have their own
characteristic preferences relations ρCk . Coalitional strategies are
also intended for needed scheduling optimization. A reduction of
the problem is allowed in which coalitions are treated as players.
Moreover, the networking relational game has a compositionality
expressed by means of the monoidal category of binary relations
[3]. The tools are monoidal operations such as disjunctive sum
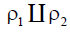 and superposition
and superposition 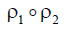 of relations correspondingly.
of relations correspondingly.
Example 1. Allow parallel 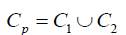 and hierarchical
and hierarchical
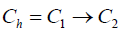 coalitions be made up of previously formed
coalitions C1,C2 . They have the following characteristic relations:
coalitions be made up of previously formed
coalitions C1,C2 . They have the following characteristic relations:
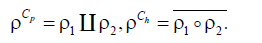
(Here, is transitive closure of ρ [3].) This is how all coalitions are built.
Every game can be gradually reduced up to receiving only one coalition C = C(Γ) representing the whole game. The latter has resulting preferences relation ρg = ρC(Γ) . Players’ communications structure Γ depends on the system of built coalitions [2, 6].
Initial dynamic game can be presented in the form of a sequence
of static subgames connected by the scale (Α, τ). They can be
solved by generalized relational Bellman’s method [6]. For the aim,
dynamic relationships 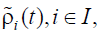 are to be built and optimized.
Sequential solution of the static subgames:
are to be built and optimized.
Sequential solution of the static subgames:

allows to build needed equilibrium scheduling 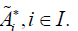 .
.
Coalitional strategies usage gives additional optimization options
to perfect the scheduling. Every coalition 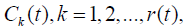 knows the tasks
knows the tasks 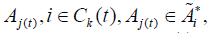 to perform. They can
be reassigned among partners
to perform. They can
be reassigned among partners 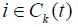 to find Pareto optimal
scheduling regarding the order
to find Pareto optimal
scheduling regarding the order 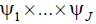 [8]. So, robots’ team
can solve autonomously any universal task (Α, τ) using distributive
control. The problem of optimal communications networking has
polynomial complexity allowing for its scalability [2].
[8]. So, robots’ team
can solve autonomously any universal task (Α, τ) using distributive
control. The problem of optimal communications networking has
polynomial complexity allowing for its scalability [2].
Messaging in the optimal network Γ∗ occurs only within effective [2] or stable coalitions [5]. The notion of coalitions stability is also defined leaning on robots’ preferences and suitability relations. A variety of types of stable coalitions gives the structure Γ∗ augmentation. This reduces uncertainty in the process of decision making.
Conclusion
In system-informational culture, artificial intelligence develops human tools in the direction of universality. It can be achieved by means of specialized intellectual robotic systems cooperation. Based on messaging, the latter allows to solve the overall universal task autonomously and under decentralized control. The problem under discussion boils down to the subtasks relational scheduling. The approach is based on the relational game solution. The simulation shows that equilibrium scheduling can be found using relational Bellman’s method. Corresponding distributive algorithm has polynomial complexity.
References
- Gromyko VI, Vasilyev NS (2018) From automatization to neurophenomenology of artificial intelligence in robotics. J. IRA 4(1): 1-2.
- Vasilyev NS (2025) On modelling of autonomous cooperative robotics in monoidal category of binary relations. WSEAS Transactions on Systems and Control 20: 109-115.
- McLane S (2004) Categories for working mathematician. Phys Math, Moscow, Russia, p. 364.
- Shoham Y, Brown KL (2008) Multiagent systems: Algorithmic, game-theoretic, and logical foundations. Cambridge University Press, New York, USA, p. 496.
- Germeyer YB (1976) Games with not opposite interests, Nauka publisher, Moscow, Russia.
- Vasilyev NS (2024) On functorial representation of optimized dynamic multiagent systems. Informatics and Applications 18(2): 2-8.
- Bellman R, Augustine OE, Nabeshima I (2014) Mathematical aspects of scheduling and applications. In: Rodin EY (Ed.), Modern Applied Mathematics and Computer Science, (1st edn), Pergamon Press, USA.
- Podinovsky VV, Nogin VD (2007) Pareto optimal solutions of multicriteria problems. Phys Mat, Moscow, Russia.
- Ur Rehman MA, Rivera S, Khan MS, Abdullah S (2024) Multi-objective optimization for load balancing and trading scheduling in networked microgrids. WSEAS Transactions on Systems and Control 23: 339-353.
- Iftar A (2024) Robust decentralized controller design for descriptor-type systems with distributed time delay. WSEAS Transactions on Systems and Control 19: 119-126.
- Thißen D, Neukirchen H (2000) Integrating trading and load balancing for efficient management of services in distributed systems. 3rd International IFIP/GI Working Conference on Trends in Distributed Systems: Towards a Universal Service Market (USM), Munich, Germany, 1890: 42-53.
© 2025 Vasilyev NS. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






