Multi-Criteria Problems of Artificial Intelligence

Artificial Intelligence (AI) systems are created in order to replace a person as a Decision Maker (DM) in this or that situation. AI systems such as robots, decision support systems, neural networks, etc. [1] operate in conditions that a person considers unfavorable for himself. Thus, a demining robot operates in an environment that is dangerous for a sapper. Decision support systems are usually used in conditions of time pressure or in aggressive environments. Neural network classifiers process volumes of information that exceed the capabilities of a human operator, etc. Replacing a person with an AI system requires the formalization of both the formulation and the process of solving the problem. Subjective factors should be excluded from the solution algorithm. A special place among such systems is occupied by those which functioning is evaluated by a set of conflicting quality criteria. When solving a specific problem of vector optimization, the decision maker creates his own model of the objective function (utility function) in accordance with his preferences. The solution of multi-criteria problems is subjective in nature, since it inevitably includes the preferences of the decision maker in terms of individual criteria and, therefore, is amenable to formalization with great difficulty.

Nevertheless, it is possible, if not to eliminate, then at least significantly reduce the influence of subjective factors on the result of solving a multi-criteria problem. It is assumed that there are some invariants, rules that are usually common to all decision makers, regardless of their individual inclinations and which they equally adhere to in a given situation. The inevitable subjectivity of the decision maker has its limits. In business decisions, a person must be rational in order to be able to convince others, explain the motives for his choice, the logic of his subjective model. Therefore, any preferences of the decision maker must be within a certain rational system. This is what makes formalization possible. There are two approaches to the formalization of multi-criteria problems. One of them is the application of the Charnez-Cooper concept [2]. This concept is based on the principle of “closer to the ideal (utopian) point”. In the space of criteria under given conditions and constraints, an a priori unknown ideal vector y^id is determined, for which the optimization problem is solved times (according to the number of particular criteria), and each time with one (next) criterion, as if there were no others at all. The sequence of “single-criterion” solutions of the original multi- criteria problem gives the coordinates of the unattainable ideal vector.

After that, the desired objective function Y( y) is introduced as a measure of approximation to the ideal vector in the space of optimized criteria in the form of some non-negative function of the vector y^id − y , for example, in the form of the square of the Euclidean norm of this vector

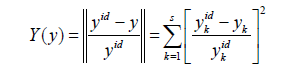
The disadvantage of this approach is the cumbersome procedure for determining the coordinates of an ideal vector. It is also important that the possibility of a dangerous approach to the limits is not excluded.

The second approach to formalization is based on the consideration of constraints. In the concept of optimality, in addition to criteria, restrictions play an equally important role, both in terms of optimization arguments x∈X and in terms of decision efficiency criteria y∈M . Even small changes can significantly affect the solution [3]. In addition, the very concept of a decision-making situation is evaluated by a measure of the dangerous approximation of individual particular criteria to their maximum permissible values. This is the basis for a possible approach to the formalization of the solution of multi-criteria problems.

In our case, the subject of research is such a subtle substance as an imaginary utility function that arises in the mind of the decision maker when solving a specific multi-criteria problem. If it exists, then each decision maker has his own utility function. Nevertheless, it is possible to obtain the prerequisites for setting a single type of meaningful model of the objective function if we identify and analyze some general patterns observed in the process of making multi-criteria decisions by different decision makers in different situations.

Without loss of generality, we will consider the case when all criteria are minimizable (the smaller they are, the better). Under some external influences, a situation may arise when one or more particular criteria approach their limitations. It is logical to consider the difference between the current value of the criterion and its maximum allowable value as a measure of the intensity of the situation:

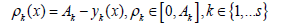
where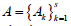 is the vector of maximum admissible minimized criteria.

If a multi-criteria decision is made in a tense situation, this means that under given external conditions one or more partial criteria, as a result of decision x, may find themselves dangerously close to their limiting values, A_k,k∈{1,...S} that is ρ_k(x) →0 . In this situation, it is necessary to do everything possible to prevent the dangerous increase in the most unfavorable (i.e., closest to its limit) partial criterion, regardless of the behavior of the others. And in a very tense situation (the first polar case: ρ_k(x)≈0 the decision maker leaves only this one, most unfavorable partial criterion in sight. Consequently, an adequate expression of the compromise scheme in the case of a tense situation is the minimax (Chebyshev) model

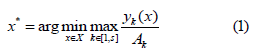
As the tension of the situation decreases, preferences for individual criteria level out. In the second polar case (ρ_k(x)≈1), the situation is so calm that the partial criteria are small and there is no threat of violating the restrictions. The decision maker here believes that a unit of deterioration in any of the relative partial criteria is fully compensated by an equivalent unit of improvement in any of the others. This case corresponds to an economical compromise scheme that ensures the minimum total losses for given conditions according to relative partial criteria. This scheme is expressed by the integral optimality model

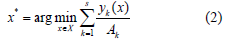
The analysis carried out reveals a pattern due to which the decision maker varies his choice from the integral optimality model (2) in calm situations to the minimax model (1) in tense situations. In intermediate cases, the decision maker selects compromise schemes that provide different degrees of satisfaction of individual criteria, in accordance with the given situation. If we accept the conclusions from the above analysis as a logical basis for formalizing the choice of a compromise scheme, then we can propose various constructive concepts, one of which is the concept of a nonlinear compromise scheme.

In contrast to the Charnes-Cooper concept, based on the principle of “closer to the utopian point,” we will consider an approach to formalizing solutions to multi-criteria problems in which the principle “away from restrictions” is fulfilled. From the standpoint of a systems approach, it is advisable to replace the task of choosing a compromise scheme with an equivalent task of synthesizing some unified scalar convolution of partial criteria, which in various situations would automatically express adequate principles of optimality. Separate models of trade-off schemes are combined into a single holistic model, the structure of which is adapted to the situation of making a multi-criteria decision. Requirements for the synthesized functionY [ y(x)]:
A. It must be smooth and differentiable;
B. In tense situations it should express the minimax principle;
C. In calm conditions-the principle of integral optimality;
D. In intermediate cases it should lead to Pareto-optimal solutions that provide various measures of partial satisfaction of the criteria.

There are several functions that can be considered that satisfy the above requirements. The simplest of them in the case of minimized criteria is scalar convolution

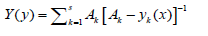
Thus, a nonlinear compromise scheme is proposed, which corresponds to a vector optimization model that explicitly depends on the characteristics of the tension of the situation:

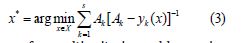
The solution of a multi-criteria problem using a nonlinear compromise scheme is carried out formally, without the direct participation of the decision maker. This solution is basic and intended for general use. If such a problem is solved in the interests of a specific person, then the basic solution can only be adjusted in accordance with the informal preferences of the decision maker.

The above analysis applies to the case of minimized criteria, were “better” means “less”. For criteria to be maximized, the unified scalar convolution has the form

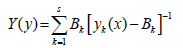
where B_k are the minimum acceptable values of the criteria to be maximized. Since the solution to a multi-criteria problem using a nonlinear compromise scheme is carried out formally, without the direct participation of the decision maker, it can be argued that such a decision is made by an artificial intelligence system.

An important type of artificial intelligence systems are neural network classifiers. They are used for technical and medical diagnostics, classification of various types of information sources, etc. In a fairly general case, the structure of a q -layered neural network classifier with direct connections is shown in (Figure 1).

Figure 1:Schematic diagram of encoder block.

Here x₁,x₂,....,x_n are the characteristics of the classification object that make up the input vector x={x_i}ⁿ_i=1;p₀=nthe number of neural elements in the receptor layer; p₁,p₂,...,p_q- the number of neurons in each of the hidden (processing) layers; p_q+1=m - number of neurons in the output layer (number of classes); y{y_k}^m_k=1-output vector of the neural network, which determines whether the classification object belongs to one of m the classes; w₁,w₂,...w_qw_q+1 - vectors of synaptic weights of the neural network.

The number of neurons p_o=n in the input layer is determined by the dimension of the input feature vector and is not subject to change. Similarly, the number of neurons in the output layer p_q+1=m is determined by the number of regions (classes) into which the feature space is divided and is also constant. The number of processing (hidden) layers q and the number of neurons in each of them p₁,p₂,...,p_q constitute the concept of the architecture [4] of a neural network and can serve as arguments (independent variables) in its optimization.

Let us limit the study to the case where the number q is fixed and given. Then the arguments for optimizing the architecture of the neural classifier are the number of neurons in each of the processing layers, which make up the vector of independent variables p{p_j}^q_j=1 The quality of functioning of the neural classifier depends on the choice of architecture p .

Let’s define quality criteria. One of the criteria is the probability of classification error. Let’s imagine it as the number of classification errors e( p) related to the total, sufficiently large number of tests N

It is assumed that as the number of neurons in the processing layers increases within some reasonable limits, the classification accuracy increases and the value of this criterion decreases. The maximum permissible network error value must be known from physical considerations and specified as a constraint f₁(p)≤A₁ .

The second criterion characterizes the time required to train a neural network with a given architecture p . There is a close correlation between this time and the total number of neurons in the hidden layers of the classifier. Therefore, we present this criterion in the form

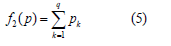
Note that this criterion also characterizes the time it takes for a signal to pass through a neural network from input to output. As the number of neurons increases, the value of the criterion increases. The maximum permissible value of the second criterion is determined by the permissible training time of the neural network and is specified as a limitation f₂(p)≤A₂. There are other criteria for characterizing various properties of a neural classifier. In this work, we will limit ourselves to only the two main criteria given, keeping in mind that the presented methodology allows for the inclusion of other properties of the classifier into consideration.

The permissible range of optimization arguments is specified by the parallelepiped constraint

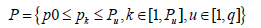
where p_u is the maximum number of neurons in the u -th layer. Thus, both criteria are contradictory, non-negative, minimized and limited. There are all the prerequisites for using scalar convolution of criteria according to a nonlinear compromise scheme as an objective function [5]. Such a convolution in the unified version is expressed by the formula

Where f(p)={f_r(p)}^r=2_r=1 is a two-dimensional vector of partial criteria. Taking into account (4), (5) and (6), the expression for the optimization problem of the neural classifier architecture is transformed into the form

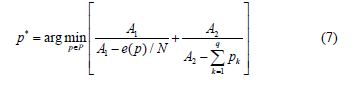
The implementation of the outlined stages of vector optimization allows, without the direct participation of the decision maker, to determine the architecture of the neural network classifier, in which conflicting criteria for the effectiveness of its functioning are systematically linked, and the resulting architecture itself is a compromise-optimal one.

The advantage of the concept of a non-linear trade-off scheme is the possibility of making a multi-criteria decision formally, which is a hallmark of artificial intelligence. The apparatus of the nonlinear trade-off scheme, developed as a formalized tool for studying systems with conflicting criteria, allows the artificial intelligence system to practically solve multi-criteria problems of a wide class.

1. Savchenko AS (2012) Methods of artificial intelligence systems: Laboratory workshop. K: NAU, p. 40.
2. Charnes A, Cooper W (1961) Management models and industrial applications of linear programming. Wiley, New York, USA, p. 240.
3. Lebedeva TT, Semenova NV, Sergienko TN (2020) Multi-criteria optimization problem: Resistance to disturbances in input data of a vector criterion. Cybernetics and System Analysis (6): 7-114.
4. George FL (2003) Artificial intelligence: Strategies and methods for solving complex problems. M. Williams, p. 864.
5. Voronin AM, Ziatdinov YK, Klimova AS (2009) Information systems will make decisions: Basic guide. K NAU, p. 136.