Parallel Ant Colony Optimization Algorithm for Robot Path Planning in Dynamic Environment

Robotics research has focused on finding solutions to the growing demand for applied robotics for the past fifty years. The concept “mobile robot” refers to a robotic system made up of a platform of moving locomotive modules that can be utilized to perform various tasks in various locations. At the moment, research in this area is focused on robot navigation in both indoor and outdoor environments in a variety of real-time applications. Also, there is a growing demand for the latest applications of intelligent robots in indoor area such as housework, surveillance, searching, safety operations in various emergency situations, and assisting handicapped or elderly people. However, there are other issues and hurdles that must be overcome before any of these applications can be further developed. Personal robotics applications in interior contexts, to be more specific, must be safe, sensitive, low-cost and above all, human- friendly. In order for autonomous robot manipulators to navigate and control their movements, they must first plan their routes. In the computing field of complexity based on time, rerouted path identification is classified as an NP-complete task. The amount of computational time required to solve a problem grows exponentially in proportion to the magnitude of the problem. Let consider a robot ‘A’ is a hard object that moves in a multidimensional workspace ‘W’, surrounded by barriers ‘B’. A big issue will be overcoming object movement and path finding while assuming there are no kinematic limitations on A’s motion (A is considered to be a “free-flying” object). The algorithm for solving this problem could be as follows. In the workspace W, primarily let we define the initial position of A and its orientation and goal position and its orientation. Second, we can generate a path that specifies a sequence of positions and orientations of A which avoids contact with B. The path could begin at the initial position and end at the goal position. If no such path exists, report it as a failure. The preceding methods have been shown to be either inefficient (due to high computational costs) or erroneous (because of local minima trapping). There have been several heuristic techniques, such as the usage of artificial neural networks, which have been created to overcome these limits.

When it comes to NP-complete issues, heuristic algorithms have the benefit of being able to find an acceptable solution rapidly, which makes them perfect for addressing them. The algorithm of ant colony optimization (ACO) employs a meta-heuristic approach that is based on biological ant behaviour observed in the real world. As one of the most effective swarm intelligent system examples, it has been used to a wide range of problems, including nonlinear objective function optimization. This paper investigates the application of the ant colony optimization method for robot path planning. Finding the fastest and safest path from one location to another is a major objective of the design of grid network (if one exists). After the optimal path has been determined in the initial (obstruction-free) network, obstacles of varying shapes and sizes are to be placed to mimic a dynamic environment, and the optimum path is determined again. The methodologies of local initialization and global initialization for pheromone re-initialization are investigated and contrasted. Using computer simulations, the ACO method is shown to be quite effective in many situations.

Literature survey

A number of studies have been published on path planning for mobile robots in static and dynamic environments. Some of the significant works are detailed in this section Cang et al. [1] shown that using mobile robots to undertake dangerous duties is a promising technology that will improve quality of life by avoiding collisions, reducing traffic jams and allowing humans to be replaced [1]. Path planning, according to Lilly [2], can be separated into two categories: Global path planning and local path planning. Agents in the mobile robot navigation environment, according to Henry et al. [3], are cognitively equipped with a high degree of autonomy and can make judgments by observing the environment in which they reside in order to reach the destination. Alhaj et al. [4] introduced a wellknown field in the discipline of control systems called intelligent control, which is a broadening of the idea of control to encompass autonomous anthropomorphic machine-environment interactions. According to Qing et al. [5], a mobile robot is a machine that can gather information from its environment and utilize that knowledge to move safely and purposefully while operating on its own. Tsui et al. [6] presented the mechanism to move a Legged robot or animallike legs, a Wheeled robot, and Tracks in real time. Grieger [7] covers path planning systems that are primarily based on software implementation. Based on Dumpster’s Expectation Maximization (EM) method, Vahid et al. [8] developed an alternative family of algorithms. For navigation in a static environment, Castillo et al. [9] describe an ACO- fuzzy based hybrid technique for mobile robot navigation. Kumar et al. [10] describe a RA-ACO-based strategy for humanoid robot navigation in a congested environment. They used Petri-Net to evaluate the suggested approach for navigation of several humanoid robots in a real-time environment and found good agreement between simulation and real-time findings. Liu et al. [11] propose a modification to improve the performance of the current ACO technique in the static environment. They used a combination of pheromone diffusion and geometric local optimization to find the best path, which resulted in the current path pheromone diffusing in the direction of the potential field force during the search-ants tend to look for a higher fitness subspace, and the pattern’s search space shrinks. Rajput et al. [12] provide yet another adjustment for the dynamic environment.

Ant colony optimization algorithm

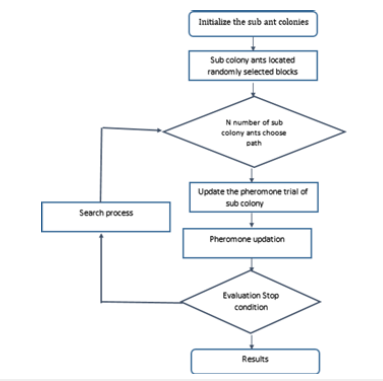
Using ant behaviour as a model, the Ant Colony Optimization (ACO) algorithms were developed to give heuristic answers to optimization problems. A well-known fact of biological ants is that they have the ability to employ collective intelligence to navigate to the most convenient source of sustenance in the real world. When looking for food, biological ants engage in complex social behaviour that is influenced by the hormones they have stored in their bodies (called pheromones). Pheromones attract other ants to the food source and draw a path for them to follow to get to the food source. A greater amount of pheromone is placed along the trail as more ants go down it, increasing the possibility that further ants will follow them. Given that more ants may traverse the trail in less time, the shortest way to the meal collects the greatest amount of pheromones. In the famous Double Bridge experiment, when given the option of choosing between a short and a long path to a food source, the ants consistently found the shortest path after a period of time. When given the option of choosing between a short and a long path to a food source, the ants consistently found the shortest path after a period of time. In addition, the pheromone diminishes over time, reducing the likelihood that more ants would follow the route. Figure 1 shows the flow chart of Parallel Ant Colony Algorithm.

Figure 1:Flow chart of parallel ant colony algorithm

Parallel ant colony algorithm-based robot path planning

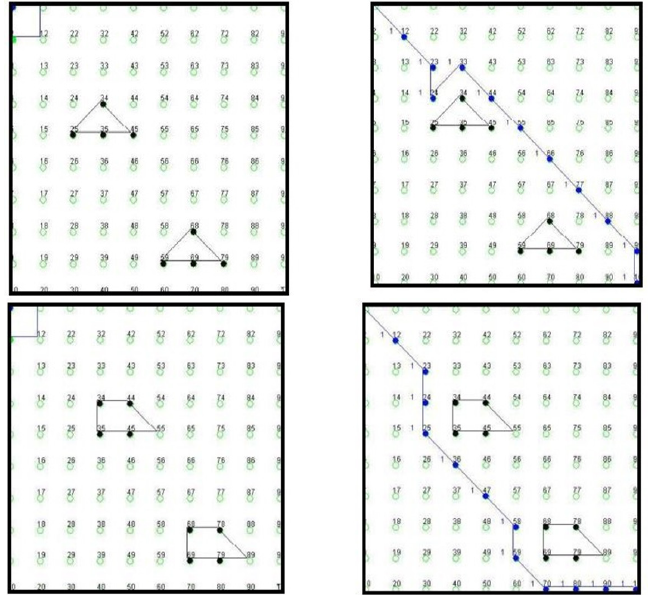
The proposed Parallel ant colony optimization algorithm [13] is used to design robot paths in a grid network in this section. The total path length is chosen as the cost or reward associated with each viable solution because our goal is to identify the shortest path between the starting and ending places. The simulation was written in Python and run on an Intel Core i3 with a 3.70GHz processor. The path optimization is done in the simulation using a 10X10 grid network. One sub colony ant is supposed to be able to occupy just one block of nodes at a time and travel to one of its adjacent nodes in one of four directions: up, down, left and right. In the network, all nodes are evenly distributed and the distance between any two adjacent nodes is normalized to 1 unit block. As a result, the length of the path is expressed in terms of the number of (unit) blocks. The simulation begins in a “clean” setting, meaning the original network contains no obstacles. The starting point is decided to be the upper-left comer, and the endpoint is chosen to be the lower-right comer. All of the pheromones are set to 0.1. The shortest path is then determined using the ant colony algorithm, and pheromones are deposited. The optimal path determined by PACO in a grid network is seen in Figure 2. Barriers (obstacles) are introduced after the algorithm has reached convergence in order to mimic a dynamic environment (for a fair comparison, the sizes of obstacles are proportional to the sizes of networks). Due to these barriers in this new network, the ACO algorithm should be invoked once more in order to identify the shortest route across it. The setting of pheromones is critical in the PACO algorithm. When the barriers are introduced into the network, the pheromones in the network are re-initialized in this study. In this work, the performance of two different re-initialization procedures, namely the global initialization and the local initialization, is evaluated and compared. During the global initialization process, all pheromones in the network are evenly reset to the original pheromone level, which is 0.1. Initialization of a “gradient” of pheromones surrounding the object is accomplished using local initialization. The value of half of the highest pheromone levels in the network is applied directly to the sites that are closest to the item. Pheromone levels decrease by a fraction of a percent for every inch that the dots move outward in a “circle” around the item (e.g., 50 percent).

Figure 2:Barriers (obstacles) are introduced after the algorithm has reached convergence in order to mimic a dynamic environment.

When compared to ACO, PACO takes less time to achieve the target without colliding with various shapes of obstacles in the surroundings. While compared to the PACO, the ACO takes slower to accomplish the goal when testing with varied shapes of obstacles in the surroundings. In several tests of varied shapes of barriers in the environment, PACO takes less time than ACO. In the overall diverse shaped obstacles, PACO (148) takes less time to accomplish the target than ACO (540). For DTA and standard DT, the SPSS program is used to find the paired sampling statistics of time to attain the target. Figure 3 shows the optimal path selection using ACO and PACO. The Mean, Standard Deviation, and Standard Error Mean are shown in Table 1.

Figure 3:Comparison of optimal path selection.

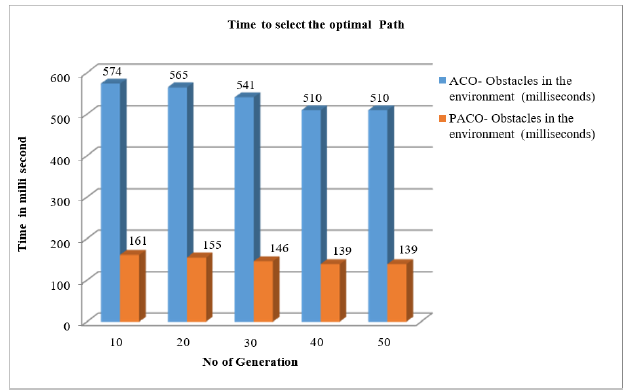
Table 1:Comparison statistics of path cost using ACO and PACO.

For robot path planning in a grid network, the parallel ant colony optimization (PACO) approach is used to determine the shortest and most collision-free route in the dynamic environment. Various forms and sizes of barriers are explored in order to accurately recreate a dynamic environment. According to this computer simulation study, the PACO approach can effectively re-route the best path for the new network if impediments are introduced into the network. Using the simulation environment, it is easy to carryout increasingly complicated networks and impediments dynamically. Path planning using the simulations are very cost effective and increasingly used in research perspective. Cost effective of the path planning is also achieved using this simulation environment and the comparison of the result with ACO could also be discussed PACO.

1. Cang Ye, Yung NC, Danwei W (2003) A fuzzy controller with supervised learning assisted reinforcement learning algorithm for obstacle avoidance. IEEE Trans Syst Man Cybern B Cybern 33(1): 17-27.
2. Lilly JH (2007) Evolution of a negative-rule fuzzy obstacle avoidance controller for an autonomous vehicle. IEEE Transactions on Fuzzy Sy 15(4): 718-728.
3. Henry H, Satish GV, Donald H (2005) Modelling social norms in multiagent systems. Journal of Experimental and Theoretical Artificial Intelligence 18(1): 49-71.
4. Alhaj A, Xiaquan L, Masoud G, Souma M, Ernest H (2003) Creative control for intelligent autonomous mobile robots. Proceedings of Intelligent Engineering Systems through Artificial Neural Networks 13: 523-528.
5. Qing Li, Zhang W, Yin Y, Wang Z, Liu G (2006) An improved genetic algorithm of optimum path planning for mobile robots. International Conference on Intelligent Systems Design and Applications 2: 637-642.
6. Tsui K, Desai M, Yanco H, Uhlik C (2011) Essential features of telepresence robots. IEEE Conference on Technologies for Practical Robot Applications, pp.15-20.
7. Grieger M (2004) A parallel implementation of path planning on reconfigurable hardware. Bielefeld University, Germany.
8. Vahid R, Saeed E, Khajehpoor P, Mirzaei P, Yousefiazar M (2007) Cooperative multi agent soccer robot team. International Scholarly and Scientific Research & Innovation 1(9): 1372-1374.
9. Castillo O, Neyoy H, Soria J, Melin P, Valdez F (2015) A new approach for dynamic fuzzy logic parameter tuning in ant colony optimisation and its application in fuzzy control of a mobile robot. Appl Soft Comput 28: 150-159.
10. Kumar PB, Sahu C, Parhi DR (2018) A hybridized regression-adaptive ant colony optimization approach for navigation of humanoids in a cluttered environment. Appl Soft Comput 68: 565-585.
11. Liu J, Yang J, Liu H, Tian X, Gao M (2017) An improved ant colony algorithm for robot path planning. Soft Computing 21(19): 5829-5839.
12. Rajput U, Kumari M (2017) Mobile robot path planning with modified ant colony optimization. Int J Bio-Inspired Comput 9(2): 106-113.
13. Junqi Yu, Ruolin Li, Zengxi F, Anjun Z, Zirui Yu, et al. (2020) A novel parallel ant colony optimization algorithm for warehouse path planning. Journal of Control Science and Engineering 5287189: 1-12.