- Submissions

Full Text
COJ Robotics & Artificial Intelligence
Fuzzy Sets Extensions and Intelligence
Kahraman C* and Boltürk E
Department of Industrial Engineering, Turkey
*Corresponding author: Kahraman C, Department of Industrial Engineering, Turkey
Submission: March 29, 2021;Published: June 03, 2021

ISSN:2832-4463 Volume1 Issue4
Abstract
It is quite hard to model human thoughts because of the lack of representation them by 0-1 logic. Fuzzy logic is a continuous and boundless valued logic whose values are between 0 and 1 and can be modeled by the fuzzy set theory. On the other hand, intelligent techniques such as machine learning, soft computing, neural networks, etc. are widely used in literature in order to better modeling and analyzing complex problems. It can be easily seen in the literature that fuzzy set theory and related extensions are integrated with these intelligent techniques. This paper illustrates a review on fuzzy sets theory and its extensions and intelligent techniques.
Keywords: Fuzzy set theory; Extensions; Intelligence; Intelligent techniques
Introduction
Intelligent systems and systems which use intelligent computing techniques are able to decide and think as human. These systems have been needed to be developed for solving complex problems where the classical methods cannot find an optimal solution. Robotics, intelligent control knowledge-based paradigms, computational intelligence, learning paradigms, soft computing including neural networks, fuzzy systems, social intelligence, ambient intelligence, computational neuroscience, artificial life, virtual worlds and society, trust management cognitive science and systems, interactive entertainment, humancentered/ human-centric computing, intelligent data analysis, knowledge management, intelligent agents, intelligent decision making and support, intelligent network security, web intelligence and multimedia are some of the problem areas that intelligent computing and intelligent systems are employed. The fuzzy sets theory was introduced by Zadeh [1] in 1965. Since ordinary fuzzy sets have been developed, a number of extensions have been proposed by many researchers. The extensions of ordinary fuzzy sets are type 2 fuzzy sets [2], intuitionistic fuzzy sets [3], fuzzy multisets [4], intuitionistic fuzzy sets of second type [5], neutrosophic fuzzy sets [6], nonstationary fuzzy sets [7], hesitant fuzzy sets [8], Pythagorean fuzzy sets [9], picture fuzzy sets [10], q-rung fuzzy sets [11], fermatean fuzzy sets [12], spherical fuzzy sets [13] and circular intuitionistic fuzzy sets [14]. These extensions have been used such as decision making, forecasting, controlling, and engineering economics with intelligent systems. In this study, we try to summarize the papers involving the integrated models of fuzzy sets and intelligent systems. The literature review with graphical illustrations is given in Section 2. Section 3 summarizes the extensions of fuzzy sets. The conclusions are given in Section 3.
Literature Review
The integration of “Fuzzy sets” and “Intelligence” concepts have been studied in the literature since 1972. In this section, we try to summarize “fuzzy sets” and “intelligence” related publications based on the Scopus database. There are 10,671 documents and these are analyzed in (Figures 1-8). Figure 1 shows the pattern of fuzzy sets and intelligence publications with respect to years. It is seen that most of the studies have been published in 2010 with a rate of 6%. It is observed that there has been an increase in number of publications since 1992. In Figure 2, the distribution of Fuzzy sets and intelligence papers by their sources are given. Most of the publications on “Fuzzy Sets” and “Intelligence” papers have been published in Lecture Notes in Computer Science Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics, Fuzzy Sets and Systems and IEEE International Conference on Fuzzy Systems, respectively. In Figure 3, the publication percentages of authors on fuzzy sets and intelligence are shown. There are 159 authors in this area and Pedrycz W, Yager RR, and Mesiar R are the leading authors on fuzzy sets and intelligence, respectively.
Figure 1: Distribution of fuzzy sets and intelligence papers with respect to years.
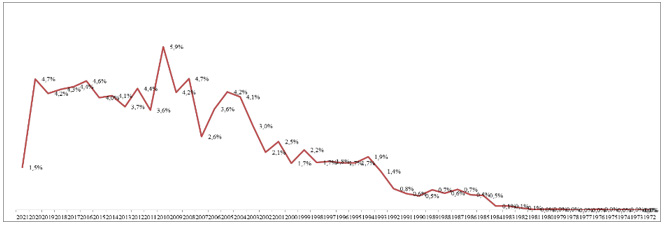
Figure 2: Fuzzy sets and intelligence publications by their published sources.
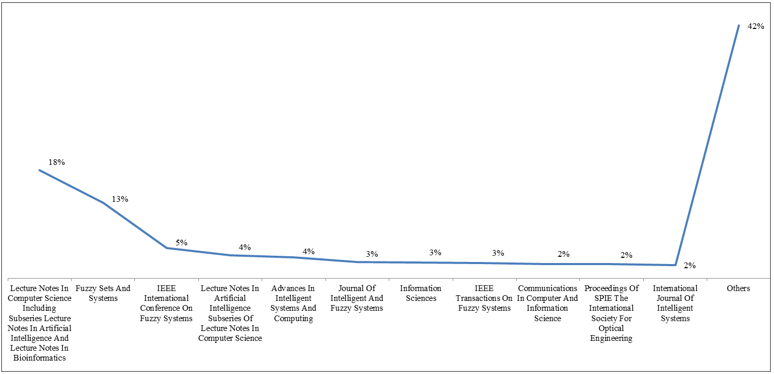
Figure 3: Publication percentages of authors on fuzzy sets and intelligence.
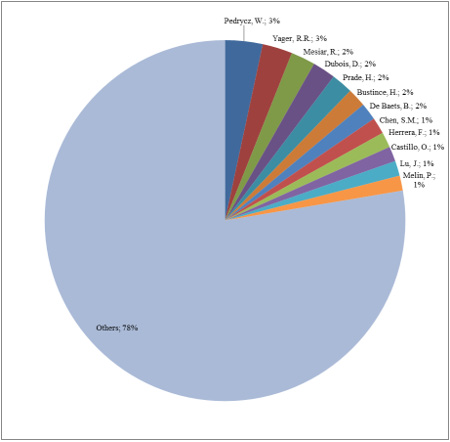
Figure 4: Distribution of fuzzy sets and intelligence publications by their countries.
Figure 5: Distribution of fuzzy sets and intelligence papers by their subjects areas.
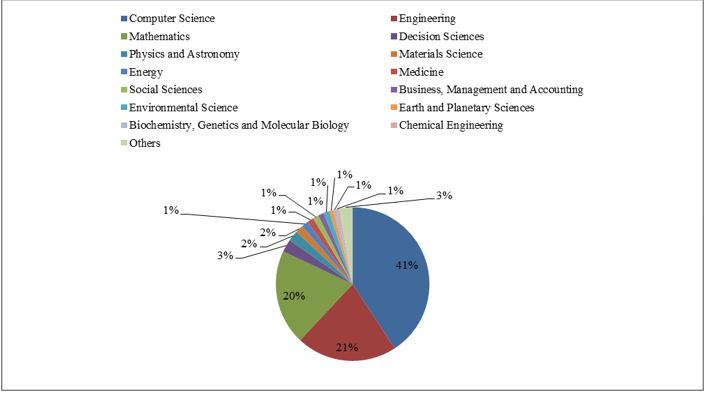
Figure 6: Percentages of publications for funding sponsors on fuzzy sets and intelligence.

Figure 7: Percentages of Publication types on Fuzzy sets and intelligence.
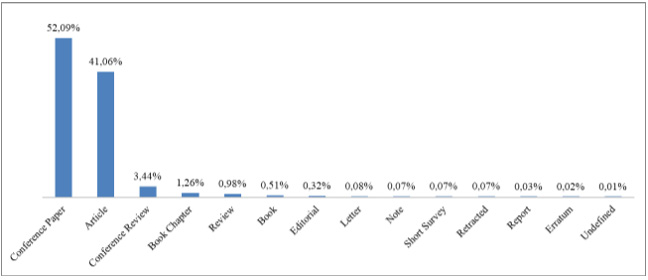
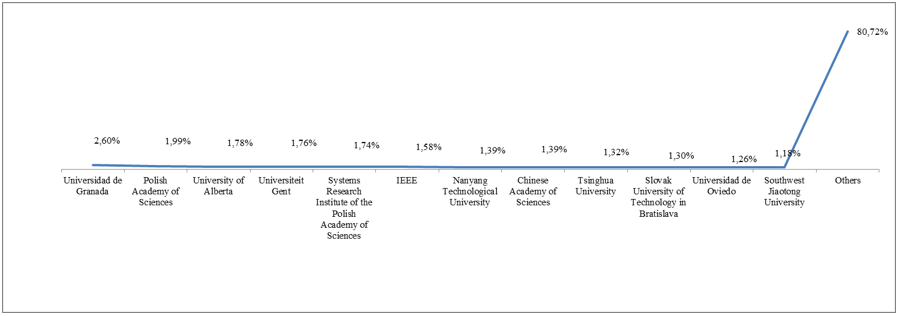
Figure 8: Percentages of affiliations those have fuzzy sets and intelligence publications.
The distribution of fuzzy sets and intelligence publications with respect to their source countries is illustrated in Figure 4. China, United States and India are the first three leaders among others.
The distribution of fuzzy sets and intelligence publications with respect to their subjects is illustrated in Figure 5. Computer science, engineering and mathematics are the first three subject areas among others. The other subjects are neuroscience, agricultural and biological sciences, chemistry, economics, econometrics and finance, arts and humanities, health professions, multidisciplinary, psychology, pharmacology, toxicology and pharmaceutics, immunology and microbiology, nursing, dentistry, and veterinary. The distribution of fuzzy sets and intelligence publications with respect to their funding sponsors is illustrated in Figure 6. National Natural Science Foundation of China is the leader among other funding sponsors. The distribution of document types on Fuzzy Sets and Intelligence are given in Figure 7. Most common types of publications are conference papers with a percentage of 52.09% and articles with a percentage of 41.06%. The distribution of affiliation has fuzzy sets and intelligence publications is illustrated in Figure 8. Universidad de Granada with a percentage of 2.6%, Polish Academy of Sciences with a percentage of 1.99 % and University of Alberta with a percentage of 1.78% are in the first three positions among other affiliations.
Extensions of Fuzzy Sets
A way of describing a fuzzy set is to list ordered pairs: an object
X and its membership degree μA (x) ∈ [0,1] in a set  . To describe
an ordinary fuzzy set, the following notation proposed by Zadeh
(1965) can be used:
. To describe
an ordinary fuzzy set, the following notation proposed by Zadeh
(1965) can be used:
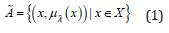
where X is the discrete universe? The non-membership degree of any x is calculated by the subtraction 1 ( ) A −μ x .
The concept of a type-2 fuzzy set was introduced by Zadeh [2] as an extension of the concept of an ordinary fuzzy set. Such sets are fuzzy sets whose membership grades themselves are fuzzy. They are very useful in circumstances where it is difficult to determine an exact membership function for a fuzzy set. A type 2 fuzzy set ≈A in the universe of discourse X can be represented by a type 2 membership function μ≈ A, shown as follows (Zadeh, 1975):
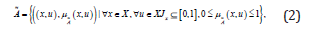
where Jx denotes an interval [0,1].
Intuitionistic fuzzy sets introduced by Atanassov [3] enable defining both the membership and non-membership degrees of an element in a fuzzy set. Their sum can be equal to or less than 1. The difference from 1, if any, is called hesitancy. Let U be a universe of discourse. An IFS I is defined as follows:
Let X be a non-empty set. An intuitionistic fuzzy set I in X is given by:
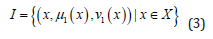
where the function μI : X → [0,1] and υI : X → [0,1] defines the degree of membership and the degree of non-membership of element to the sets I, respectively, with the condition that.
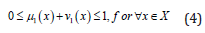
The degree of hesitancy is calculated as follows:
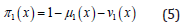
Yager [4] first discussed fuzzy multi-sets, although he uses the term of fuzzy bag; an element of X may occur more than once with possibly the same or different membership values. Assume X is a set of elements. Then a fuzzy bag A drawn from X can be characterized by a function . A Count Mem such that
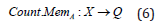
where Q is the set of all crisp bags from the unit interval.
Smarandache [6] developed neutrosophic logic and
neutrosophic sets (NSs) as an extension of intuitionistic fuzzy sets.
The neutrosophic set is defined as the set where each element of
the universe has a degree of truthiness, indeterminacy and falsity.
The sum of these degrees can be at most equal to 3 since each of
them can be independently at most equal to 1. Let E be a universe.
A neutrosophic set 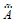 in E is characterized by a truth-membership
function TA , a indeterminacy-membership function A I , and a falsitymembership
function FA .
in E is characterized by a truth-membership
function TA , a indeterminacy-membership function A I , and a falsitymembership
function FA .
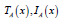 and
and  are real standart elements of [0,1]. A
neutrosophic set
are real standart elements of [0,1]. A
neutrosophic set 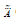 can be given by Eq. (17):
can be given by Eq. (17):
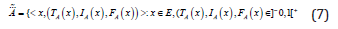
There is no restriction on the sum of 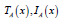 and
and  , so
that
, so
that 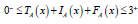 .
.
Nonstationary fuzzy sets are introduced by Garibaldi and
Ozen [7]. Let A denote a fuzzy set of a universe of discourse X
characterized by a membership function μA . Let T be a set of time
points ti (possibly infinite) and 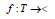 denote the perturbation
function. Associates with each element (t, x) of T × X a time specific
variation of
denote the perturbation
function. Associates with each element (t, x) of T × X a time specific
variation of 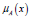 . The nonstationary fuzzy set
. The nonstationary fuzzy set 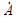 is denoted by
is denoted by
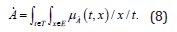
Hesitant fuzzy sets introduced by Torra [8] allow many potential degrees of membership of an element to be assigned to a set. These fuzzy sets force the membership degree of an element to be possible values between zero and one. A hesitant fuzzy set on X can be defined as in Eq. 9:
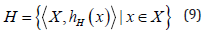
where hH(x) is a set of hesitant fuzzy elements whose membership values are in [0,1].
Pythagorean fuzzy sets (PFSs) are an extension of intuitionistic
fuzzy sets and it allows researchers to assign membership and nonmembership
degrees in a wider area. Atanassov’s intuitionistic
fuzzy sets of second type (IFS2) or Yager’s Pythagorean fuzzy
sets [9] are characterized by a membership degree and a nonmembership
degree satisfying that their squared sum is equal to or
less than one, which is a generalization of intuitionistic fuzzy sets.
This provides a larger area than IFS in order to assign membership
and non-membership degrees [5]. Let ∪ be a universe of discourse.
A PFS 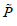 is an object having the form,
is an object having the form,
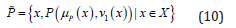
where 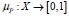 is the membership degree and
is the membership degree and 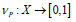 is the non-membership degree. Then, Eq. (11) is valid:
is the non-membership degree. Then, Eq. (11) is valid:
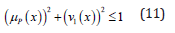
The degree of indeterminacy is defined as follows:

IFS has been extended to picture fuzzy sets (PiFS). PiFS based
approaches are more effective methods to meet different human
views such as yes, abstain, no, and refusal. PiFS based models
are successful in symbolizing uncertain information in different
processes such as cluster analysis and pattern recognition.
Cuong [10] introduced picture fuzzy sets (PiFS) which are direct
extensions of intuitonistic fuzzy sets. A picture fuzzy set 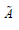 on the
universe X is an object of the form.
on the
universe X is an object of the form.

where 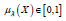 is called the “degree of positive
membership of
is called the “degree of positive
membership of 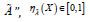 is called the “degree of neutral
membership of
is called the “degree of neutral
membership of 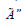 and
and 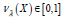 is called the “degree of
negative membership of
is called the “degree of
negative membership of 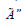 and
and 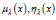 , and
, and 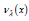 satisfy
the following condition:
satisfy
the following condition: 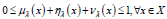 . Then for
. Then for 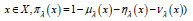 could be called the degree of
refusal membership of x in
could be called the degree of
refusal membership of x in  . Thereafter,
. Thereafter, 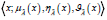 will
be given as
will
be given as 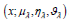
Voting can be a good illustration of such a situation as the human voters may be divided into four groups of those who: vote for, hesitant, and vote against, refusal of the voting.
Q-Rung orthopair fuzzy sets (QROFSs) introduced by Yager [11] are represented with the degree of membership and non-membership. In q-ROFSs, the sum of the qth power of the membership and non-membership degrees must be at most equal to one.
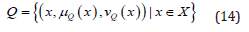
where the function 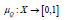 denotes the degree of
membership and
denotes the degree of
membership and 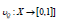 denotes the degree of non-membership
of the element x∈ X to the set Q, respectively, with the condition that
denotes the degree of non-membership
of the element x∈ X to the set Q, respectively, with the condition that 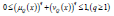 for every x∈ X . The degree of indeterminacy is given as
for every x∈ X . The degree of indeterminacy is given as 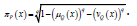
When q = 3, Senapati and Yager [12] have called q-rung orthopair fuzzy sets as fermatean fuzzy sets (FFSs).
Let X be a universe of discourse. A Fermatean fuzzy sets F in X is an object having the form:
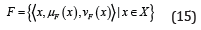
where 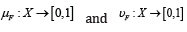 which includes the
circumstance
which includes the
circumstance
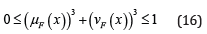
for all x∈ X . The numbers μF(x) and vF(x) indicate, respectively, the degree of membership and the degree of non-membership of the element x in the set F . For any FFS F and x∈ X , the degree of hesitancy is calculated as follows:

Spherical fuzzy sets (SFS) have been recently introduced by Gundogdu K, et al. [12]. These ets are based on the fact that the hesitancy of a decision maker can be assigned satisfying the condition that the squared sum of membership, non-membership and hesitancy degrees is at most equal to 1. In the following, definition of SFS is presented:
Single valued Spherical Fuzzy Sets (SFS) 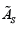 of the universe of
discourse U is given by
of the universe of
discourse U is given by
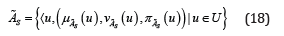
where
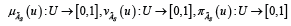
and
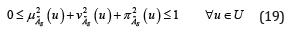
For each u , the numbers 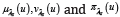 are the degree of
membership, non-membership and hesitancy of to
are the degree of
membership, non-membership and hesitancy of to 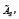 respectively.
respectively.
Conclusion
A problem under imprecise and vague environment can be defined by fuzzy sets. More than 20 new extensions of fuzzy sets such as spherical fuzzy sets and circular intuitionistic fuzzy sets have been proposed in the literature for better expressing experts’ thoughts by including additional parameters in membership and non-membership functions. It is observed that these parameters have been successfully used in modeling human thoughts. In this paper, it is observed that fuzzy sets and intelligence are widely used in today’s technologies. In the future, it is thought that with the new extensions, use of fuzzy sets will increase with the integration of intelligence techniques.
References
- Zadeh LA (1965) Fuzzy sets. Information Control 8(3): 338-353.
- Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning. Information sciences 8(3): 199-249.
- Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy sets and Systems 20(1): 87-96.
- Yager RR (1986) On the theory of bags. International Journal of General System 13(1): 23-37.
- Atanassov KT (1989) More on intuitionistic fuzzy sets. Fuzzy Sets and Systems 33(1): 37-45.
- Smarandache F (1999) A unifying field in logics: Neutrosophic probability, set and logic. Rehoboth: American Research Press, Champaign, USA.
- Garibaldi JM, Ozen T (2007) Uncertain fuzzy reasoning: A case study in modelling expert decision making. IEEE Transactions on Fuzzy Systems 15(1): 16-30.
- Torra V (2010) Hesitant fuzzy sets. International Journal of Intelligent Systems 25(6): 529-539.
- Yager RR (2013) Pythagorean fuzzy subsets. Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS). Edmonton, Canada.
- Cuong BC (2014) Picture fuzzy sets. Journal of Computer Science and Cybernetics 30(4): 409-420.
- Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst 25(5): 1222-1230.
- Senapati T, Yager TT (2019) Fermatean fuzzy sets. J Amb Intell Hum Comput 11: 663-674.
- Gündoğdu K, Kahraman FC (2019) Spherical fuzzy sets and spherical fuzzy TOPSIS method. Journal of Intelligent and Fuzzy Systems 36(1): 337-352.
- Atanassov KT (2020) Circular intuitionistic fuzzy sets. Journal of Ambient Intelligence and Smart Environments 39(5): 5981-5986.
© 2021 Kahraman C. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






