Reduced (Twisted) Group C*-Algebras without Nontrivial Ideals

The class of group operator algebras was a typical model Murray and von Neumann studied in initiating the theory of operator algebras [1-8]. Since then, the interplay between groups and operator algebras has been a main line in the development of operator algebras. In this article, we review the recent work on determining when a countable discrete group is C*-simple, i.e., its reduced group C*algebra has no nontrivial closed two side ideas. We also discuss the question for twisted group algebras. All groups in this article are assumed to be countable and discrete. Let G be a group.

The left regular unitary representation λ G→ B(l (G)) 2 : is defined by (λ( g)ξ)(h) = ξ( g −1h) , for all g, h∈G and ξ ∈l2(G) . The C*-algebra generated by {λ ( g) : g∈G } is the reduced group C*-algebra of G denoted by C*_T(G) .

In 1949, I. Kaplansky asked R. Kadison whether any simple unital C*-algebra other than C has a nontrivial projection. In 1968, Kadison suggested R. Powers to study from this point of view the reduced group C* algebra C*_T(F₂) of the non-abelian free group with two generators. Powers showed within a week that is simple and published the work several years later [9,10]. Since then, considerable efforts have been made in finding C*-simple groups. The generalization/modification of Powers’ proof had been the only method in finding C*-simple groups until M. Kalantar and M. Kennedy’s breakthrough work [6].

Recall that an action of a group G on a compact Hausdorff space X is said to be strongly proximal if for each probability measure μ on X, the week ∗-closure of the orbit G.μ contains a point-mass δx, for some x∈X . An action G ∩ X is a boundary action if it is strongly proximal and minimal. In this case, we call X a G-boundary. Recall also that the amenable radical Rad(G) of a group G is defined as the largest normal amenable subgroup of G.

The following Furman’s result gives the existence of boundary actions of a group.

Let G be a group and t∈G . Then t /∈ Rad(G) if and only if there is a G-boundary X such that t acts non-trivially on X.

An action G ∩ X is free if = ∈ = =∅ g X { x X : gx x } for every non-identity g∈G . An action G ∩ X is topologically free if = ∈ = X_g { x X : gx x } has an empty interior for every non-identity element g∈G . Kalantar and Kennedy proved in [6] that a discrete group G is C*- simple if and only if G acts topologically freely on some G-boundary. By Proposition 2.5 in [3], the action of G on its universal boundary ∂_FG is free if it is topologically free. Hence, we have the following characterization of C*-simple groups.

A group G is C*-simple if and only if G acts freely on some G-boundary X. A subgroup H of group G is recurrent if there is a finite subset F ⊆G\{e}such that F ∩ gHg⁻¹ =∅, ∀g∈G . Kennedy [7] obtained the following intrinsic characterization of C*-simple groups.

A group is C*-simple if and only if it has no amenable recurrent subgroups.

U. Haagrep [5] characterized C*-simple groups in terms of Dixmier-type properties.

Let G be a group. Then G is C*-simple if and only if for all t₁,....,t_m ∈ G\{e},

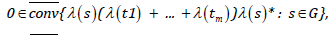
Where conv is the closure of all convex combinations of the elements in the set.

The theory of twisted group C*-algebras is closed related to projective unitary representations of groups with important applications in various fields of mathematics and physics [9].

Let G be a group and π : G → U(H) , where U(H) is the unitary group of Hilbert space H. We say that π is a projective unitary representation of G if

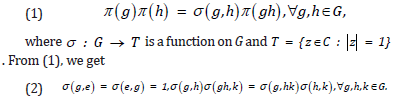
A function σ : G → T is called a 2-cocycle on G if it satisfies (2). The above described representation π is called a σ-projective unitary representation of G. We define λσ : G → U(l² (G)) by

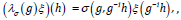
Let π : G → U(H)be a σ-projective unitary representation of G and ξ ∈H . The map ϕ : g π ( g)ξ ,ξ is called a diagonal matrix coefficient of π. Given two σ-projective unitary representations π and ρ of a group G, say that π is weakly contained in ρ, write π  ρ , if any diagonal matrix coefficient of π is a limit of sums of diagonal matrix coefficients of ρ, uniformly on every finite subsets of F. We say that π is weakly equivalent to ρ, write π ∼ ρ , if π  ρ and ρ π

Determining when C^∗_r (Gσ), is simple a very popular question in operator algebras. There are many discussions on this topic. For instance, Bedos and Omland [2] gave some sufficent conditions for C^∗_r (Gσ), be to simple. They also applied their results to different types of groups such as wreath products and Baumslag-Solitar groups. Very recently, we used weak containment of projective unitary representations to give a characterization of the simplicity of C^∗_r (Gσ)

The algebra * σ r C (G, ) is simple if and only if for every σ-projective unitary representation π of G, if π_σ λ then π ∼λ_σ

1. An G, Gao M (2022) Simple reduced twisted group C*-algebras.
2. Bedos E, Omland T (2018) On reduced twisted group C*-algebrad that are simple and/or have a unique trace. J Noncommut Geom 12: 947-996.
3. Breuillard E, Kalanta M, Kennedy M, Ozawa N (2017) C*-simplicity and unique trace property for discrete groups. Publications Math. De l’IHES 126: 35-71.
4. Furman (2003) On minimal strongly proximal actions of locally compact groups. Israel J Math 136: 173-187.
5. Haagerup U (2016) A new look at C*-simplicity and the unique trace property of a group. Operator Algebras and Applications, Springer Publishers, Germany 12: 61-70.
6. Kalantar M, Kennedy M (2017) Boundaries of reduced C*-algebras of discrete groups. J Reine Angew Math (Crelles Journal) 727: 247-267.
7. Kennedy M (2020) An instrinsic characterization of C*-simplicity. Ann Sci Norm Supr 53: 1105-1119.
8. Murray F, Neumann J (1936) On rings of operators. Ann of Math 37(1): 116-229.
9. Packer J (2008) Projective representations and the Mackey obstruction-- A survey. Group representations, ergodic theory, and mathematical Physics: A tribute to Goerge W Mackey. Contemporary Mathematics 449: 345-378.
10. Powers R (1975) Simplicity of the C*-algebra associated with the free group on two generators. Duke Math J 42(1): 151-156.