A Survey: Non-Fragile Controller for T-S Fuzzy System

Introduction

Recent years have witnessed rapidly growing popularity of fuzzy control systems in engineering applications. The numerous successful applications of fuzzy control have sparked a flurry of activities in the analysis and design of fuzzy control systems. The Takagi and Sugeno (T-S) fuzzy model, proposed in Takagi and Sugeno (1985) for the purpose of function approximation, can be reformulated as a fuzzy dynamic model to represent nonlinear dynamic systems. This model consists of a set of local linear models that are smoothly connected by nonlinear fuzzy membership functions. This fuzzy modeling method provides an alternative approach to describing complex nonlinear system and drastically reduces the number of rules in modeling higher-order nonlinear systems. Consequently, T-S fuzzy models are less prone to the curse of dimensionality than other fuzzy models, in particular conventional fuzzy systems. And more important, T-S fuzzy models provide a fundamental basis for development of systematic tools for stability analysis and controller design of fuzzy control systems in view of powerful conventional control theory and techniques.
In the area of nonlinear control systems design, an important approach is to model the considered nonlinear systems as Takagi and Sugeno (T-S) fuzzy models by a set of If-Then rules, which are formed from linguistic variables and values and by quantifying the meaning of the linguistic values using membership functions”, the T-S fuzzy model can be obtained. Compared with conventional modeling techniques which use a single model to describe the global behavior of a nonlinear system, fuzzy modeling is essentially a multi-model approach in which simple sub-models are fuzzily combined to describe the global behavior of a nonlinear system.
Digital control systems design has become an important field in electrical engineering and in systems and control theory. One of the important and fundamental issues in digital control systems design is the filter or controller coefficient sensitivity because even vanishingly small perturbations n controller or filter coefficients may destabilize the resulting systems. In the actual engineering systems, the controllers or filters realized by microprocessors/microcontrollers do have some uncertainties due to limitations in available microprocessor/microcontroller memory, effects of Finite Word Length (FWL) of digital processors, quantization of the A/D and D/A converters, and so on. Therefore, non-fragile (insensitive) control is becoming popular in many fields of engineering and science.
It is known that control systems are designed for robustness with respect to plant parameters or designed for the optimization of a single performance measure; many designed control systems require accurate controllers. Thus, when implementing a desired controller, all the controller coefficients are required to be with the exact values as those to be designed, which, however, is not always possible in practical applications since finite word length and round-off errors in numerical computations by computers are frequently encountered. Motivated by the above concerns, in this thesis, the problem of non-fragile control, to design a controller for T-S fuzzy system which can tolerate some perturbations in feedback controller gains, has been addressed.

Non-Fragile Control

With the rapid development of computer and automation technologies, more and more attention is paid to the digital control system which has been considered as one of the most important and active fields in the research. A typical configuration of the digital control system is shown in Figure 1, in which limitation in available microprocessor memory, effects of Finite Word Length (FWL) of the digital processor, errors for truncation and quantization of the A/D and D/A converters, and so on, always cause the controller parameters trivial deviations from the original design values [1]. Keel & Bhattacharyya [2], by means of numerical examples, have shown that the controllers designed by using weighted H∞, μ, and L1 synthesis techniques may be very sensitive, or fragile with respect to relatively small perturbations in controller parameters. Therefore, a significant issue is how to design a filter or controller for a given plant such that the filter or controller is insensitive to some errors with respect to its coefficients, that is, the designed filter or controller is insensitive or non-fragile.

Figure 1: A typical digital control system configuration.

D/A quantization

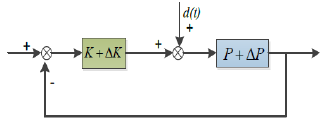
The configuration shown in Figure 2 simply describes the robust control. Figure 3 shows the non-fragile control, while the robust non-fragile control is shown in Figure 4, where P denotes the plant, ΔP stands for the uncertainties of the plant P, K denotes the controller, and ΔK denotes the inaccuracies or uncertainties in the implementation of a designed controller. There are two main types of coefficient uncertainties considered in the designed methods. One is of a norm-bounded type; the other is of an interval-bounded type. Furthermore, the above two types also can be divided into additive case and multiplicative case. Then, the models of the uncertainty ΔK are given as follows: Sensitivity analysis allows us to assess the effects of changes in the parameter values [3,4]. Hence, it is very useful to understand how changes in the parameter values influence the design. After the hard work of many researchers in more than one-decade, fundamental results have been obtained for the study of sensitivity analysis and performance limitations in automatic control systems ([see, for example, 5,6], and the references therein), and many different definitions of sensitivity have been used for sensitivity analysis [7]. One of the effective synthesis methods is the coefficient sensitivity method, which describes the variations in performance due to variations in the parameters that affect the system dynamics [8]. It is well known that very small perturbations in the coefficient of the designed controller or filter may result in the serious deterioration of the system performance, including instability. Therefore, the controller or filter should be designed to be insensitive to some amount of error with respect to its coefficients. Sensitivity theory is always used to characterize the phenomenon of trivial deviations, which motivates us to design insensitive controllers and filters in the framework of coefficient sensitivity theory, because the coefficient variations resulted from the limitation of the available computer memory are of trivial deviations.

Figure 2: A robust control configuration.

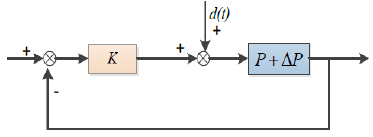
Figure 3: A non-fragile control configuration.

Figure 4: A robust non-fragile control configuration.

Fuzzy Models and Fuzzy Systems

Fuzzy models or fuzzy systems are rule based or knowledgebased models or systems originating from the concepts of fuzzy sets, fuzzy IF-THEN rules, and fuzzy reasoning. A typical fuzzy system, especially in applications of fuzzy logic control, consists of four components: knowledge base or fuzzy rule base, inference engine, fuzzification interface, and defuzzification interface [9]. Figure 5 shows the block diagram of the structure of a fuzzy system.
The knowledge base or fuzzy rule base contains a set of fuzzy IF-THEN rules and a database. The database is the declarative part of the knowledge base that describes the definition of the objects (facts, terms) and the definition of the membership functions used in the fuzzy rules. The fuzzy rules are the procedural part of the knowledge base that contains information on how these objects can be used to infer conclusions.

Figure 5: Basic structure of fuzzy systems.

The inference engine, which is the central component of a fuzzy system and performs the inference procedure upon the fuzzy rules and given conditions to derive conclusions.
The fuzzification interface (or fuzzifier) is a mechanism to transform a real-valued variable into a fuzzy set. It is well known that a crisp value of an input can be transformed into a fuzzy set in the form of a fuzzy singleton that has zero membership function value everywhere except at the particular point where the membership function value is unity. The fuzzification interface employing the technique of fuzzy singleton has been widely adopted in fuzzy control applications. In fact, the observed inputs in typical fuzzy control applications are always of crisp values. The fuzzification interface scales these crisp values, transforms the range of values of the input variables to their corresponding universes of discourse, and then converts the scaled input values into suitable linguistic values that can be defined as a fuzzy set (fuzzy singleton). This method of fuzzification is efficient and simple, and easily implemented. This typical process of fuzzification, often used in fuzzy control applications, is usually called the singleton fuzzification and the corresponding interface is called the singleton fuzzifier.
On the other hand, the defuzzification interface (or defuzzifier) is a mechanism to transform a fuzzy set over an output universe of discourse to a real-valued variable. The objective of defuzzification is to extract a crisp value that best interprets a fuzzy set. The most frequently used defuzzifiers include the center of gravity (or the center of area), center average, and maximum defuzzifiers, among many others.
With crisp inputs and outputs, it has been shown that a fuzzy system is in fact a nonlinear mapping from its input space to its output space. More specifically, a fuzzy system describes a transformation from a set of linguistic fuzzy IF-THEN rules, which are often described in natural language, into a mathematical nonlinear mapping, which is often described by a precise mathematical function. It is this attractive and useful feature of fuzzy systems that leads to their wide application in a variety of disciplines, in particular, in fuzzy control applications.

Brief Review of Fuzzy Logic Control

Conventional Fuzzy Control (Mamdani-Type Fuzzy Control)

Mamdani and Assilian developed the first real fuzzy control algorithm in the early 1970s [10], where control of a small steam engine was considered. The fuzzy control algorithm basically consisted of a set of heuristic control rules, and fuzzy sets and fuzzy logic were used, respectively, to represent linguistic terms and to evaluate the control rules, called conventional fuzzy control or Mamdani-type fuzzy control, which is given in Figure 6. Since then, similar fuzzy logic control algorithms have been developed for many different engineering processes. For example, Kickert and Lemke developed a fuzzy control algorithm for a warm-water plant, and Ostergaard presented another fuzzy control algorithm for a small-scale heat exchanger. There were many other applications of conventional fuzzy control, including robot, stirred tank reactor, traffic junction, steel furnace, cement kilns automobile, wastewater treatment missile autopilot, motor, network traffic management and congestion control, and so on [11-13]. In addition, conventional fuzzy control was also widely used in various consumer electronic devices such as video cameras, washing machines, televisions, and sound systems in the late 1980s and early 1990s.

Figure 6: Input-output membership function.

These methods of conventional fuzzy control are essentially heuristic and model free. Conventional fuzzy logic control has been widely accepted by engineers in industry due to its simplicity and ease in understanding and implementation. The fuzzy control “IFTHEN” rules are often obtained based on an operator’s control action or knowledge. It is thus obvious that the design method works well only in the cases where operators or their knowledge play an important or critical role in controlling the system. Even though the performance of such control schemes might be generally satisfactory in practice, the stability issue of the closed-loop fuzzy control systems is often not addressed and thus often criticized in the earlier development of these methods. Moreover, design of conventional fuzzy control systems suffers from a lack of systematic tools, which often leads to difficulty in controller design and inconsistency in performance of the closed-loop control systems. Thus, great efforts have been devoted to issues of stability analysis and controller design of conventional fuzzy control systems, and various approaches have been developed.
In addition to a heuristic approach provided by Braae and Rutherford (1979) for stability analysis of fuzzy control systems, a key idea of most approaches is to consider a fuzzy controller as a nonlinear controller and embed the stability or control design problem of fuzzy control systems into conventional nonlinear system stability theory. The typical approaches include describing function approach [14], cell-state transition [15], Popov‟s theorem [16], and circle criterion [17], among others. However, a general theory for systematic stability analysis and controller synthesis of conventional fuzzy control systems is still out of reach and remains a challenging task for the fuzzy control community.

Takagi-Sugeno Model-based fuzzy control

The Takagi and Sugeno (T-S) fuzzy model, proposed in Takagi and Sugeno (1985) for the purpose of function approximation, can be reformulated as a fuzzy dynamic model to represent nonlinear dynamic systems [18]. This model consists of a set of local linear models that are smoothly connected by nonlinear fuzzy membership functions. This fuzzy modeling method provides alternative approach to describing complex nonlinear systems [19], and drastically reduces the number of rules in modeling higherorder nonlinear systems [20]. Consequently, T-S fuzzy models are less prone to the curse of dimensionality than other fuzzy models, in particular conventional fuzzy systems. And more important, T-S fuzzy models provide a fundamental basis for development of systematic tools for stability analysis and controller design of fuzzy control systems in view of powerful conventional control theory and techniques (see Figure 7).

Figure 7: Model-based fuzzy control design.

A great number of theoretical results on function approximation, stability analysis, and controller synthesis have been developed for Takagi-Sugeno fuzzy models during the last 10 years or so. It has been shown that T-S fuzzy models are universal function approximates in the sense that they are capable of approximating any smooth nonlinear functions to any degree of accuracy in any convex compact region [21]. This result provides a theoretical foundation for using T-S fuzzy models to represent complex nonlinear systems approximately or quite often to represent complex nonlinear systems in practice most accurately. On the basis of this function approximation capability of T-S fuzzy models, a variety of stability analysis and controller design approaches has been developed for T-S fuzzy systems by exploiting the particular structure of these models and conventional control techniques such as Lyapunov stability theory [22,23].

References

1. Guo XG, Yang GH (2009) Non-fragile H_∞ filter design for delta operator formulated systems with circular region pole constraints: An LMI optimization approach. Acta Autom Sin 35(9):1209-1215.
2. Keel LH, Bhattacharyya SP (1997) Robust, fragile, or optimal. IEEE Trans. Automatic Control 42(8): 1098-1105.
3. Castillo E, Minguez R, Castillo C (2008) Sensitivity analysis in optimization and reliability problems. Reliable Eng Syst Saf 93(12):1788-1800.
4. Castillo E, Gutierrez JM, Hadi AS (1997) Sensitivity analysis in discrete Bayesian networks. IEEE Trans Syst Man Cybern Part A Syst Humans 27(4): 412-423.
5. Chevrel P, Yagoubi M (2004) A parametric insensitive H2 control design approach. Int J Robust Nonlinear Control 14(15): 1283-1297.
6. Hilaire T (2009) Low-parametric-sensitivity realizations with relaxed l2-dynamic-range-scaling constraints. IEEE Trans. Circuits Syst.-II: Express Briefs 56(7): 590-594.
7. Hilaire T, Chevrel P, Whidborne JF (2010) Finite word length controller realizations using the specialised implicit form. Int J Control 83(2): 330-346.
8. Zhang BY, Zhou SS, Li T (2007) A new approach to robust and non-fragile H infinty control for uncertain fuzzy systems. Information sciences 177: 5118-5133.
9. Lee CC (1990) Fuzzy logic in control systems: Fuzzy logic controller. I. IEEE Trans Syst Man Cybern 20(2): 404-418.
10. Mamdani EH, Assilian S (1975) An experiment in linguistic synthesis with a fuzzy logic controller. Int J Man Mach Stud 7: 1-13.
11. Wang Y, Hao S, Karimi HR, Duan D (2018) Notice of violation of IEEE publication principles: Dissipativity-based fuzzy integral sliding mode control of continuous-time T-S fuzzy systems. IEEE Trans on Fuzzy Syst 26(3): 1164-1176.
12. Zhang D, Han QL, Jia X (2017) Network-based output tracking control for a class of T-S fuzzy systems that cannot be stabilized by non-delayed output feedback controllers. IEEE Trans. on Cyber., 45(8):1511-1524.
13. Liu G, Zhang Q, Ding Z (2005) Non-fragile H-infinite control for T-S fuzzy systems via LMI. International Conference on Control & Automation.
14. Kickert WJM, EH Mamdani (1978) Analysis and design of a fuzzy logic controller. Fuzzy Sets Syst 1: 29-44.
15. Kang H (1993) Stability and control of fuzzy dynamic systems via cell-state transitions in fuzzy hypercubes. IEEE Trans Fuzzy Syst 1(4): 267-279.
16. Furutani E, Saeki M, Araki M (1992) Shifted Popov criterion and stability analysis of fuzzy control systems. Proc 23^rd IEEE Conf Decision and Control, Tucson, AZ, pp. 2790-2795.
17. Singh S (1992) Stability analysis of discrete fuzzy control systems. Proc 2^nd IEEE Int Conf on Fuzzy Systems, San Diego, USA, pp. 527-534.
18. Cao SG, Rees NW, Feng G (1997) Analysis and design for a class of complex control systems - Part I: Fuzzy modeling and identification, Automatica 33: 1017-1028.
19. Tanaka K, Wang HO (2001) Fuzzy control systems design and analysis: A LMI Approach. Wiley, New York, USA.
20. Sugeno M (1999) On stability of fuzzy systems expressed by fuzzy rules with singleton consequents, IEEE Trans Fuzzy Syst 7(2): 201-224.
21. Xu JX, Hang CC, Liu C (2000) Parallel structure and tuning of a fuzzy PID controller. Automatica 36(5): 673-684.
22. Dan Z, Nguang SK, Srinivasan D, Li Yu (2018) Distributed filtering for discrete-time T-S fuzzy systems with incomplete measurements. IEEE Trans on Fuzzy Syst 26(3):1459-1471.
23. Bo P, Cai Y, Zhang W (2017) LMI relaxations for quadratic stabilization of guaranteed cost control of T-S fuzzy systems. Int J Fuzzy Syst 19(5): 1-14.