- Submissions

Full Text
COJ Electronics & Communications
MHD Stagnation Point Flow of a Jeffrey Fluid Over a Stretching/Shrinking Sheet Through Porous Medium
Eswara Rao M1 and Krishna Murthy M2*
1 Dept of Mathematics, Sri Venkateswara University, India
2 Dept of Mathematics, GITAM Deemed to be University, India
*Corresponding author: Krishna Murthy M, Dept of Mathematics, GITAM Deemed to be University, Bengaluru, Karnataka, India
Submission: August 29, 2018;Published: October 30, 2018

ISSN 2640-9739 Volume1 Issue3
Abstract
In this analysis the MHD stagnation point flow of Jeffrey fluid over a stretching/shrinking sheet through porous medium is studied. The governing partial differential equations are transformed into nonlinear ordinary differential equation using the similarity transformations and are solved shooting technique. The effects of governing parameters on the velocity, the temperature and the concentration while the skin friction coefficients, the rate of heat transfer are studied graphically
Keywords: MHD; Jeffrey fluid; Stretching/shrinking sheet; Porous medium
Introduction
Many fluids such as a blood, dyes, ketchup, shampoo, clay cooling, mud, polymer melts certain oils and greases etc., have complicated relations between stress and strain. Such fluids don’t obey the Newton’s law of viscosity and are usually called non- Newtonian fluids. The study of non-Newtonian fluids has gained interest because of their numerous technological applications, including manufacturing of plastic sheets, performance of lubricants, transpiration cooling, thermal oil recovery and movement of biological fluids. The mass transfer analysis in boundary layer flow is of great importance in extending the theory of separation processes and chemical kinetics. The boundary layer flow of non-Newtonian fluids due to a stretching surface has gained much importance in many engineering and industrial applications that include both metal and polymer sheet. The reason for such acceleration interest is due to its wide occurrence in various applications such as biological sciences, geophysics, chemical and petroleum industries etc. In view of their differences with Newtonian fluids, several models of non-Newtonian fluids have been proposed by various researchers. Among these, the Jeffrey model is a rate type of non-Newtonian fluid which can describe the characteristic of relaxation and retardation times.
Flow in the boundary layer on a continuous solid surface with constant speed was studied by Sakiadis [1]. Due to entrainment of ambient fluid, this boundary layer is different from that in Blasius flow past a flat plate. Erickson et al. [2] extended this problem to the case where suction or blowing existed at the moving surface. Crane [3] considered the moving strip whose velocity is proportional to the distance from the slit. These types of flow usually occur during the drawing of plastic films and artificial fibers. The heat and mass transfer on a stretching sheet with suction or blowing was investigated by Gupta & Gupta [4]. They dealt with the isothermal moving plate and obtained temperature and concentration distributions. The problems of the flow through stretching surface have been investigated by Wang [5]. Dutta et al. [6] analyzed temperature distribution in the flow over a stretching sheet with uniform heat flux. They have shown that temperature at a point decreases with an increase in the Prandtl number. Recently, Kartini et al. [7] discussed by Mixed convection Jeffrey fluid flow over an exponentially stretching sheet with magnetohydrodynamic effect. Maria et al. [8] studied MHD Convective Flow of Jeffrey Fluid Due to a Curved Stretching Surface with Homogeneous Heterogeneous Reactions. Effects of diffusion-thermo and thermo-diffusion on two-phase boundary layer flow past a stretching sheet with fluid-particle suspension and chemical reaction, a numerical study by Krupa Lakshmi et al. [9].
In fluid dynamics, the stagnation point flow and flow over a stretching surface are important in theoretical and applications point of view. In fluid dynamics, stagnation is a point in a flow field where the local velocity of the fluid is zero. Stagnation points exist at the surface of objects in the flow field, where the fluid is brought to rest by the object. Stagnation flow towards a stretching sheet is investigated by Wang [10]. Mixed convection MHD stagnation point flow on vertical, linearly stretching sheet is explained by Ishak et al. [11-13]. The steady two-dimensional stagnation point flow on a stretching sheet was first discussed by Chaim [14]. Stagnation point flow over a stretching surface is explained by Mahapatra & Gupta [15]. Recently Awaludin et al. [16] studied the Stability analysis of stagnation-point flow over a stretching/shrinking sheet. Santosh & Mohan [17] presented by the Heat and mass transfer by MHD flow near the stagnation point over a stretching /shrinking sheet in a porous medium. Dash et al. [18] studied the Numerical approach to boundary layer stagnation-point flow past a stretching/shrinking sheet. Mohamed El-Aziz [19] examined the Dual solutions in hydromagnetic stagnation point flow and heat transfer towards a stretching/shrinking sheet with non-uniform heat source/sink and variable surface heat flux. Aini Mat et al. [20] investigate the Boundary Layer Stagnation-Point Slip Flow and Heat Transfer towards a Shrinking/Stretching Cylinder over a Permeable Surface. Fauzi [21] worked on Stagnation point flow and heat transfer over a nonlinear shrinking sheet with slip effects. Agbaje [22] studied a new numerical approach to MHD stagnation point flow and heat transfer towards a stretching sheet. Hayat et al. [23] investigated the MHD stagnation point flow of Jeffrey fluid by a radially stretching surface with viscous dissipation and Joule heating. Bhatacharyya [24] has studied the Dual solution in boundary layer stagnation point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. He has considered the fluid to be electrically non-conducting.
Heat transfer in porous media has received considerable attention and has been the field of a number of investigations during the last two decades. The need for fundamental studies in porous media heat transfer stems from the fact that a better understanding of a host of thermal engineering applications in which porous materials are present is required. Some of examples of thermal engineering disciplines which stand to benefit from a better understanding of heat and fluid flow processes through porous media are geothermal systems, thermal insulations, grain storage, solid matrix heat exchangers, oil extraction and manufacturing numerous products in the chemical industry. The application of electromagnetic fields in controlling the heat transfer as in aerodynamic heating leads to the study of magneto hydrodynamic heat transfer. This MHD heat transfer has gained significance owing to recent advancement of space technology. The MHD heat transfer can be divided in two parts. One contains problems in which the heating is an incidental by product of electromagnetic fields as in MHD generators and pumps etc., and the second consists of problems in which the primary use of electromagnetic fields is to control the heat transfer. Heat transfer in channels partially filled with porous media has gained considerable attention in recent years because of its various applications in contemporary technology. These applications include porous journal bearing, blood flow in lungs or in arteries, nuclear reactors, porous flat plate collectors, packed bed thermal storage solidification of concentrated alloys, fibrous and granular insulation, grain storage and drying, paper drying, and food storage. Besides the use of porous subtracts to improve heat transfer in channels, which is considered as porous layers, finds applications in heat exchangers, electronic cooling, heat pipes, filtration and chemical reactors etc. In these applications engineers avoid filling entire channel with a solid matrix to reduce the pressure drop. Recently, Rao & Sreenadh [25] studied the MHD Boundary Layer Flow of Jeffrey Fluid over a Stretching/Shrinking Sheet through Porous Medium. Vishnu et al. [26] analyzed the Darcy-Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and Ohmic dissipations effects. Baag et al. [27] Entropy generation analysis for viscoelastic MHD flow over a stretching sheet embedded in a porous medium. Hayat et al. [28] studied the Heat Source/ Sink in a Magneto-Hydrodynamic non-Newtonian Fluid Flow in a Porous Medium: Dual Solutions. Vajravelu et al. [29] discussed the effect of heat transfer on the nonlinear peristaltic transport of a Jeffrey fluid through a finite vertical porous channel. Ali et al. [30] worked on the Analytic Solution for Fluid Flow over an Exponentially Stretching Porous Sheet with Surface Heat Flux in Porous Medium by Means of Homotopy Analysis Method. Ruchika et al. [31] studied the Multiple solutions of MHD boundary layer flow and heat transfer behavior of nanofluids induced by a power-law stretching/ shrinking permeable sheet with viscous dissipation.
Mathematical Formulation of the Problem
Figure 1:Physical model of the problem 2 λ .
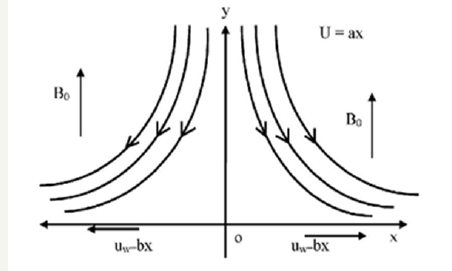
A steady tow dimensional boundary layer flow of a Newtonian incompressible electrically conducting fluid near a stagnation pointover a stretching /shrinking surface placed in the plane y = 0 of Cartesian coordinate system in a saturated porous medi um. The x -axis is taken along the surface with origin at the stagnation point and y -axis is perpendicular to it. A uniform magnetic field of strength 0 B is assumed to be applied in the positive y -direction normal to the plate. The magnetic Reynolds number of the flow is taken to be small enough, so that induced magnetic field negligible in comparison with applied one Figure 1. The system of boundary layer equations is of the following is
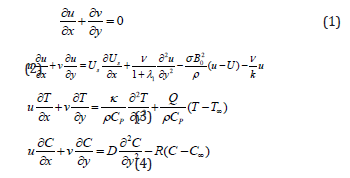
The boundary conditions are
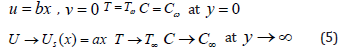
Similarity Transformations
The continuity equation (1) is identically satisfied but introducing a stream function ψ (x, y) such that
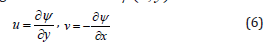
The momentum energy and concentration equations (2), (3) and (5) can be transformed into the corresponding ordinary differential equations by introducing the following dimensionless variables are
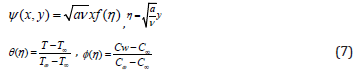
Incorporating equations (6) and (7) into the governing equations (2) and the boundary conditions (5) we finally obtain a system of non-linear ordinary differential equations with appropriate boundary conditions are of following.
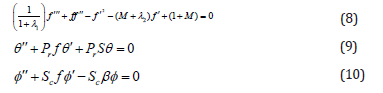
And the boundary conditions are
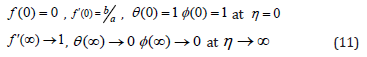
Where primes denote differentiation with respect to η
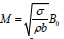 magnetic parameter,
magnetic parameter,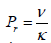 Prandtl number
Prandtl number 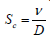 Schmidt number,
Schmidt number,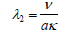 porous parameter λ1Jeffrey parameter, S=heat source parameter
and
porous parameter λ1Jeffrey parameter, S=heat source parameter
and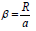 the non-dimensional reaction rate of solutal.
the non-dimensional reaction rate of solutal.
Physical quantities of interest are skin friction coefficient Cf , local rate of heat transfer coefficient u N and local Sherwood number Sh which are defined as
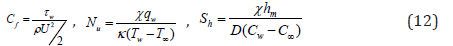
The wall shear stress w τ the heat flux w q and mass flux m h are defined as

Using the similarity variables equations (6) and (7) we obtain

Where 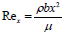
Results and Discussion
The present steady on MHD Jeffrey fluid flow over a stretching/ shrinking sheet through porous medium is investigated. The governing equations (2), (3) and (4) are solved using Runge-kutta method along with shooting technique. The pertinent governing parameters on velocity f ′(η ) , temperature and concentration through graphs are shown in Figures (2)- (4.10) while numerical values of the rate of heat transfer is presented in tabular form.
Figure 2:The velocity profile for shrinking sheet and different values of .

The velocity f ′(η ) distribution is presented through the Figures 2 and 3 in case of shrinking sheet. The velocity f ′(η ) distribution various values of Jeffrey parameter λ1 and porous parameter λ2 are shown in Figure 2. We observed that velocity is decreases with the increasing values of λ2 for both Newtonian and non-Newtonian case. From Figure 3 shows that the velocity f ′(η ) distribution for different values of the effects of velocity ratio b/a i.e. stretching rate of the bounding surface b and straining rate of the stagnation point flow a (a>0). We observed that the velocity decreases with increasing values of b/a for both cases.
Figure 3:The velocity profile for different values of b/a .
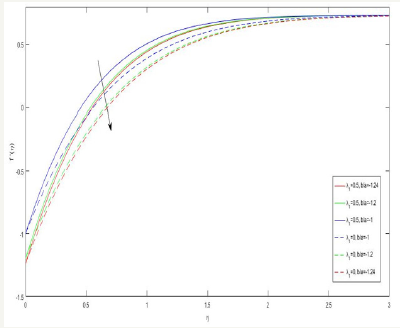
Figure 4:The temperature distribution for different values of b/a .
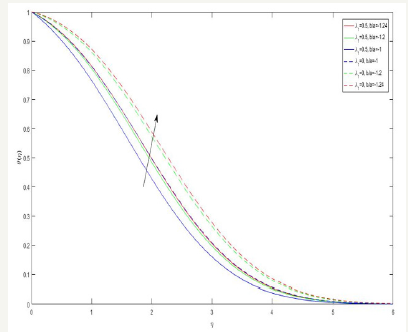
The temperature distribution is presented through Figure 4-7 in case of shrinking sheet. The temperature distribution for various values of the effect of velocity ratio b/a is shown in Figure 4. We observe that the temperature is increases with increasing b/a for exhibit the effect of heat source parameter S on temperature distribution. It reveals that the temperature increases with increasing S. and a hike in temperature is marked hear the plate when the viscosity and conductivity of the fluid the same porosity. From Figure 6 depicts the effect of velocity ratio b/a on temperature gradientθ ′(η ) . It seems that the temperature gradient θ ′(η ) is increases with b/a up to while the opposite behavior at till end of the plate. Figure 7 indicate that temperature decreases with increasing r P for both cases.
Figure 5:The variation of s on the temperature distribution.

Figure 6:The variation of b/a on temperature gradient.
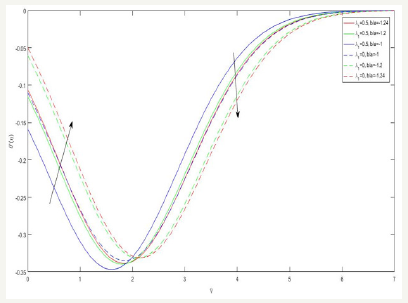
Figure 7:The temperature distribution for different values of Pr.
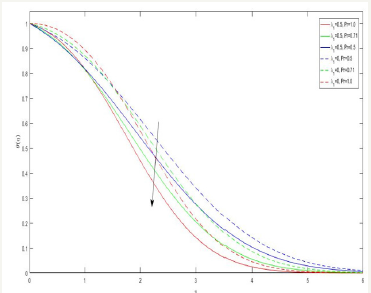
Figure 8:The variation of b/a on concentration profile.
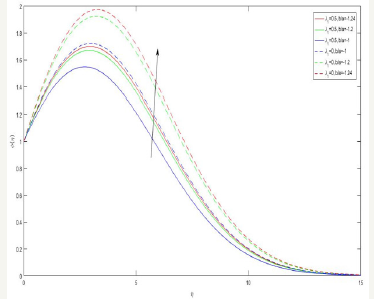
Figure 9:The variation of Sc on concentration profile.
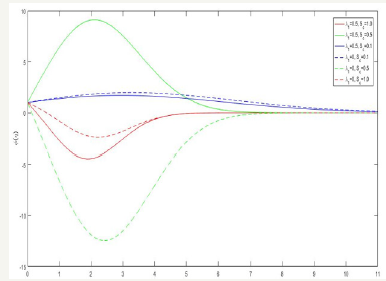
Figure 10:The variation of Sc on concentration gradient profile.
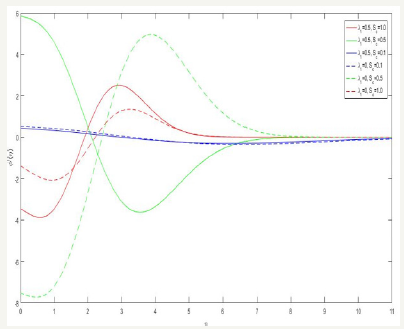
Figure 8-10 exhibits the profiles related to concentration and its gradient the concentration φ (η ) for various values b/a is displayed in Figure 8. It shows that the concentration φ (η ) increases with increasing values of b/a for both Newtonian ( λ1 = 0 ), and non-Newtonian cases ( λ1 = 0 .5). Figure 9 is devoted to bring out the effect of Schmidt number Sc. It shows that the concentration φ (η ) increases with increasing Sc for both cases. Figure 10 exhibit the effect of Schmidt number Sc on concentration gradient φ ′(η ) increases at the surface with increasing Sc for both cases.
Table 1:The rate of heat transfer -θ’(0) for different values of b/a.
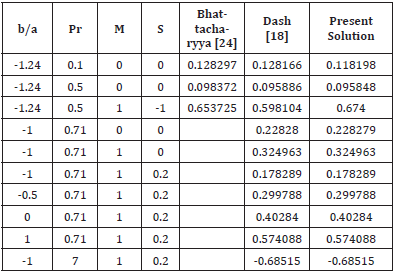
The flow characteristic at the bounding surface are vital in determine the flow stability. Table 1 shows the rate of heat transfer for stretching/shrinking of the plate surface. It is seen from the table the Nusselt Number (Nu) decreases with an increase in the value of Pr in the absence of Jeffrey parameter ( λ1 = 0 ),, porous parameter ( λ2 = 0 ), Magnetic field parameter (M=0) and heat source (s = 0), but it increases in the presence of magnetic field parameter but the reverse effect is observed with an increase in the value of source parameter. Further, it is seen that an increase in magnitude of shrinking rate in the presence of both magnetic field parameter and heat source, Nu decreases. The Nusselt number remains positive in the presence of sink (s=-1). It is intersecting to note that for an aqueous medium for higher value of Pr (Pr=7.0), the Nusselt number Nu assumes negative value. It is to note that an increase in stretching rate and Prandtl number (Pr) both contribute to increase the rate of heat transfer but Pr contributes significantly. Moreover, in case of shrinking sheet high Prandtl number fluid causes a thermal instability at the surface (i.e. negative value of Nu) whereas no such case arises for stretching sheet.
References
- Sakiadis BC (1961) Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J 7: 26-28.
- Erickson LE, Fan LT, Fox VG (1966) Heat and mass transfer on a moving continuous flat plate with suction and injection. Industrial & Engineering Chemistry Fundamentals 5(1): 19-25.
- Crane LJ (1970) Flow past a stretching plate. Z Angew Math Phys 21(4): 645-647.
- Gupta PS, Gupta AS (1977) Heat and mass transfer on a stretching sheet with suction or blowing. The Canadian Journal of Chemical Engineering 55(6): 744-746.
- Wang CY (1984) The three-dimensional flow due to a stretching flat surface. Physics of Fluids 27(8): 1915-1917.
- Dutta BK, Roy P, Gupta AS (1985) Temperature field in flow over a stretching surface with uniform heat flux. International Communication in Heat Mass Transfer 12(1): 89-94.
- Kartini A, Zahir H Anuar I (2016) Mixed convection Jeffrey fluid flow over an exponentially stretching sheet with magnetohydrodynamic effect. AIP Advances 6(3): 035024.
- Maria I, Tasawar H, Ahmed A (2016) MHD convective flow of jeffrey fluid due to a curved stretching surface with homogeneous heterogeneous reactions. Journal Pone 11(9).
- Krupa Lakshmi KL, Gireesha BJ, Rama SRG, Mahanthesh B (2016) Effects of diffusion-thermo and thermo-diffusion on two-phase boundary layer flow past a stretching sheet with fluid-particle suspension and chemical reaction: A numerical study Journal of the Nigerian Mathematical Society 35(1): 66-81.
- Wang CY (2008) Stagnation flow towards a shrinking sheet. International Journal of Non-Linear Mechanics 43(5): 377-382.
- Ishak A, Nazar R, Pop I (2007) Mixed convection on the stagnation point flow toward a vertical, continuously stretching sheet. Journal of Heat Transfer 129(8): 1087-1090.
- Ishak A, Nazar R, Pop I (2008) Post stagnation point boundary layer flow and mixed convection heat transfer over a vertical, linearly stretching sheet. Archives of Mechanics 60(4): 303-322.
- Ishak A, Jafar K, Nazar R, Pop I (2009) MHD stagnation point flow towards a stretching sheet. Physica A: Statistical Mechanics and its Applications 388(17): 3377-3383.
- Chiam TC (1998) Heat transfer in a fluid with variable thermal conductivity over a linearly stretching sheet. Acta Mechanica 129(1998): 63-72.
- Mahapatra TR. Gupta AS (2003) Stagnation Point Flow towards a Stretching Surface. Canadian Journal of Chemical Engineering, 81(1-2), 258-263.
- Awaludin IS, Weidman PD, Ishak A (2016) Stability analysis of stagnation-point flow over a stretching/shrinking sheet. AIP Advances 6(4).
- Chaudary S, Choudhary MK (2016) Heat and mass transfer by MHD flow near the stagnation point over a stretching /shrinking sheet in a porous medium. Indian Journal of pure and Applied Physics 54: 209-217.
- Dash GC, Tripathy RS, Rashidi MM, Mishra SR (2016) Numerical approach to boundary layer stagnation-point flow past a stretching/ shrinking sheet. Journal of Molecular Liquids 221: 860-866.
- El-Aziz MA (2016) Dual solutions in hydromagnetic stagnation point flow and heat transfer towards a stretching/shrinking sheet with nonuniform heat source/sink and variable surface heat flux. Journal of the Egyptian Mathematical Society 24(3): 479-486.
- Aini Mat NA, Arifin NM, Nazar R, Bachok N (2015) Boundary layer stagnation-point slip flow and heat transfer towards a shrinking/ stretching cylinder over a permeable surface. Applied Mathematics 6(3): 466-475.
- Fauzi NF, Ahmad S, Pop I (2015) Stagnation point flow and heat transfer over a nonlinear shrinking sheet with slip effects. Alexandria Engineering Journal 54(4): 929-934.
- Agbaje TM, Mondal S, Makukula ZG, Motsa SS, Sibanda P (2015) A new numerical approach to MHD stagnation point flow and heat transfer towards a stretching sheet. Ain Shams Eng J 9(2): 233-243.
- Hayat T, Waqas M, Shehzad SA, Alsaedi JA (2015) MHD stagnation point flow of Jeffrey fluid by a radially stretching surface with viscous dissipation and Joule heating. Hydrol. Hydromech 63(4): 311-317.
- Bhatacharyya k (2011) Dual solution in boundary layer stagnation point flow and mass transfer with chemical reaction past a stretching/ shrinking sheet. Int Commun Heat Mass Transfer 38(7): 917-922.
- Eswara RE, Sreenadh S (2017) MHD boundary layer flow of jeffrey fluid over a stretching/shrinking sheet through porous medium. Global Journal of Pure and Applied Mathematics 13(8): 3985-4001.
- Ganesh NV, Abdul Hakeem AK, Ganga B (2016) Darcy-Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and Ohmic dissipations effects. Ain Shams Eng J.
- Baag S, Mishra SR, Dash GC, Acharya MR (2016) Entropy generation analysis for viscoelastic MHD flow over a stretching sheet embedded in a porous medium. Ain Shams Engineering Journal 8(4): 623-632.
- Hayat T, Awais M, Imtiaz A (2016) Heat source/sink in a magnetohydrodynamic non-newtonian fluid flow in a porous medium: dual solutions. PLOS ONE 11(9): e0162205.
- Vajravelu K, Sreenadh S, Lakshminarayana P, Sucharitha G (2016) Effect of heat transfer on the nonlinear peristaltic transport of a Jeffrey fluid through a finite vertical porous channel. International Journal of Biomathematics 9(2): 1-24.
- Ali A, Zaman H, Abidin MZ, Naeemullah, Shah SIA (2015) Analytic solution for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium by means of homotopy analysis method. American Journal of Computational Mathematics 5(2): 224- 238.
- Ruchika D, Puneet R, Lokendra K (2015) Multiple solutions of MHD boundary layer flow and heat transfer behavior of nanofluids induced by a power-law stretching/shrinking permeable sheet with viscous dissipation. Powder Technology 273: 62-70.
© 2018 Krishna Murthy M. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






