Natural Limitations of Quantum Computing

Introduction

Macro time

We will introduce a model of how a digital computer functions in general. It is based on the idea that a computer can be only in a finite number of states and that in proceeding through the processing of information, a computer processes string. The program is a sort of a mechanism or a transition function that moves the computer from one state to another state. The input symbols, the output symbols and the intermediate strings are themselves states. Any state of a computer can be thought of as a cellular grid. At any given moment, each cell would contain a bit; either zero or one. Although the total number of all possible states is very big, yet the topology of the set of all possible states is the discrete topology. A given processing operation is defined as a subset of the set of all possible states. The state that identifies a computer at a given moment is, from the physical point of view, independent of the previous and the following states; although, it is, from the logical point of view, interrelated to them. In any computer, it is necessary to provide a group of timing signals which are present in a set sequence and which may then be used to gate various computer circuits. These gating signals provide an automatic means of stepping the computer circuits through a fixed routine to carry out all the necessary smaller steps to execute some instruction of a program. Timing signals are obtained using special devices. For the aims of this paper, we will now expand on these facts with the emphasis on the timing property of the signals under consideration. According to our model, the computer leaps from one state to another. This leap takes place whenever a timing signal is provided. The special devices used for creating the timing signals are based on natural physical laws, yet the signals themselves are, in a sense, artificial. They are intended to fulfil the requirements of a preferential design . According to the aforementioned, we are justified in attributing the macro time trait to these signals. With this nomenclature, we are borrowing from the notion of irreversible time which is manifested by aging in the passage from birth to death. The fact that every living creature die is the most tangible evidence for the flux of time [1-4]. We find in the writings of the Persian philosopher scientist- poet Omar Khayyam:

“The moving finger writes; and, having writ, Moves on not all you Piety nor Wit. Shall lure it back to cancel half a Line, nor all your Tears wash out a Word of it.”

How can this irreversible time be reconciled with the microscopic world described by “timeless” entities? Will we be able someday to overcome this irreversibility? According to classical physics, time is a background of space. Relativity unified space and time in a four-dimensional continuum known as spacetime. Alas, this continuum lacks any reference or background. The basic idea here is that Einstein substituted the three-dimensional ether with a four dimensional one. The Bulgarian engineer Nikola Kalitzin [1] came to the rescue by introducing a fifth time dimension. Noting that he created by this another new ether, Prof. Kalitzin introduced a sixth time dimension, and went on to introduce more and more extra time dimensions. He formulated what is known as the multitemporal theory of relativity in which the four-dimensional continuum bears to the new five-dimensional continuum the same relation to the four-dimensional formalism of Einstein as is the case with the latter in reference to the three-dimensional physical space. Prof. Kalitzin suggested the idea that it is also possible for the quantum phenomena to be explained by the multitemporal the- ory of relativity, e.g. a particle may be at one point with respect to sometime dimension, and at a second point with respect to another time dimension.

Since a single bit is assigned to a cell of the constructive grid at each moment, the efficiency of a computer increases by increasing the number of cells and decreasing the volume of each cell. Can we go on decreasing the volume of each cell till we arrive at the stage where a single atom or electron constitutes a cell? The answer is no. That is because of Heisenberg’s uncertainty principle which implies that it is not possible to prepare an atom or an electron in a state for which the results of physical measurements are certain. The certainty of such measurements is a prerequisite for assigning a single bit to each atom or electron cell. This means that Heisenberg’s uncertainty principle places an absolute limit on the power of information processing. That was not the case for Richard Feynman who discovered that the intrusion of quantum effects offers a fantastic computational opportunity. This is imputed to quantum entanglement. If a physical system, composed of identifiable states, carries correlations between the states, and these correlations can be realized in two or more ways, the state of the composite system is a superposition of the different ways to realize the correlation and the state is said to be entangled. We replace here the single bit of the classical computer by the set of the identifiable states. Put simply, an entangled quantum state can contain more information than could possibly exist in any classical state involving the same number of particles. The qubit is the quantum analog of a bit. Any quantum system which two states has at least can serve as a quantum bit [5-8].

The most essential property of quantum states when used to encode bits is the possibility of coherence and superposition, the general state being

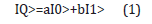
with IaI2 +IbI2 =1. What this means is not that the value of a qubit is somewhere between zero and one, but rather that the qubit is a superposition of both states and, if we measure the qubit we will find it with probability IaI2 to carry the value zero and with probability IbI2 to carry the value one. In a well-known experiment, we consider a source which emits a pair of particles such that one particle emerges to the left and the other one to the right. The source is such that the particles are emitted with opposite momenta. According to the design of the experiment, there will be two beams of particles: an upper one and a lower one. If the particle emerging to the left, which we call particle 1, is found in the upper beam, then particle 2 travelling to the right is always found in the lower beam. Conversely, if particle 1 is found in the lower beam, then particle 2 is always found in the upper beam. In the qubit language we would say that the two particles carry different bit values. Either particle 1 carries zero and then particle 2 definitely carries one, or vice versa. Quantum mechanically, this is a two-particle superposition state of the form

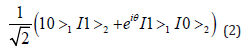
The phase θ is just determined by the internal properties of the source and we assume for simplicity θ = 0 . Equation (2) describes an entangled state. The interesting property is that neither of the two qubits carries a definite value, but what is known from the quantum state is that as soon as one of the two qubits is subject to a measurement, the result of this measurement being completely random, the other one will immediately be found to carry the opposite value. In a nutshell this is the conundrum of quantum non-locality, since the two qubits could be separated by arbitrary distances at the time of measurement [9].

Quantum Computing

A quantum computer is a physical system, but one that runs according to quantum physics not classical physics, to realize a computation. If we use a quantum computer, we can operate simultaneously on all possible binary input strings of any length N. In other words, we can run a single computation on all possible inputs in parallel. Moreover, a quantum computer has the power to create a virtual reality simulation indistinguishable from the original. This is since, computation in a quantum universe is completely different from computation in a classical universe. Our universe is a quantum universe. A quantum universe is irreducibly random, it is an inexhaustible source of information, a bottomless reservoir of surprise. If computational systems are a natural consequence of physical laws, then a quantum computer is inevitable. Many scientists and engineers around the world are working very hard in a quest to build a prototype device that would demonstrate the power of quantum computing. There is a difficulty that renders fruitless all the efforts invested in building a quantum computer till now [10,11].

The difficulty is incorporated by the requirement that the device must operate in a completely reversible way. Our world runs forwards in time rather than backwards. If a quantum computer is to run in a reversible way, it must remain isolated from the outside world during the computation. At no stage can the computer leave a record of which computational path it has followed, a record that a passing classical observer may or may not read. At no stage can the interaction of the quantum computer with the outside world result in the determination of the path followed by the quantum computer. It is a basic principle of quantum computing to leave the quantum computer to itself without any outside intervention while processing prepared states of data (prepared according to quantum rules). Yet the design of a quantum algorithm includes the necessity of timing signals. It is presupposed that these signals click from outside the quantum computer [12]. They are, in a sense, artificial.

All quantum algorithms work with the following basic framework:

1. The system starts with the qubits in a classical state.

2. From there the system is put into a superposition of many quantum states.

3. This is followed by acting on this superposition with several unitary operators. It is well known that a unitary operator is reversible.

4. In this last stage, a measuring operator is applied to the final superposition.

As we mentioned above, the whole quantum computer must be isolated without any interaction, whatsoever, with the rest of the world. The timing signals are external and result in decoherence, hence they cannot be used to decide whether the instant for applying a certain operator has come and thereby applying it. Programming a collection of operators to be executed one after another necessitates the import of a corresponding ordered collection of timing signals. Stage 4 above puts forth another difficulty: how can we take hold of our desired result through the application of a measuring operator. It is impossible to examine all the component states in the final superposition. This is because such an examination necessitates a supply of timing signals, a click for each eigenvalue of the measuring operator. Moreover, it is well known that the measurement operation ends up with one of the component states only. If we wish to take hold of some definite component state of the final superposition, we must index all the component states of the final superposition. If such an indexing is to be feasible, we must invoke macro time as the main reference factor in the indexing process.

In any real quantum computing one must assume an interaction between the quantum system used and its’ environment, i.e. decoherence. This has negative consequences for the possibility of having error-free quantum computation. A variety of methods have been developed for designing quantum error-correcting codes. After a quantum state is entangled with the environment and an error occurs, one can then determine, by a measurement, the erroneous subspace into which the erroneous state has fallen, without destroying the erroneous state, the error can then be undone using a unitary transformation. But insertion of the correcting code is a type of an interaction between the quantum system and its’ environment. Applying the necessary operators for undoing the errors cannot be realized without providing external timing signals. This is a fundamental problem. The physical isolation of the quantum computer entails, according to quantum physics, its’ informative isolation. No body must know what is going on, including the possibility of the occurrence of errors, and their correction. According to quantum theory, there exist processes by which one can learn the results of a computation without actually performing the computation, provided the possibility of performing that computation is available, even though computation itself is not performed.

Micro Time

That physics has encountered consciousness cannot be denied. The continuing discussion by physicists of the connection of consciousness with quantum physics displays that encounter. Here is how physics Nobel laureate Eugene Wigner once put it: When the province of physical theory was extended to encompass microscopic phenomena through the creation of quantum mechanics, the concept of consciousness came to the fore again. It was not possible to formulate the laws of quantum mechanics in a fully consistent way without reference to the consciousness. Quantum theory claims that if you observed an atom to be some place, it was your looking that caused it to be there-it was not there before you saw it. Does that apply to big things? In principle yes. This means that we must not scrutinize the flow of operations of the quantum computer unless we guess that it reached the stage of final superposition.

Once Sir James Jeans said: The universe begins to look more like a great thought than a great machine. Suppose that the nucleus is subjected to continuous measurement in order to determine at what moment in time it decays. Under such conditions the nucleus will never decay. According to quantum mechanics, the wave function describes the entirety of a system manifested as a superposition of states. The wave function propagates across all venues and exists at all times. But as a measurement takes place, the wave function collapses at a given point in space and time. This collapse, although random, may help define a flux of time in the micro world. But not exactly, that is because the collapse is initiated by the measurement process which is a macro process. This will be especially evident if we remember that only conscious minds pop wave functions and that the happenings of the micro world are isolated from the macro world.

What about the no-cloning theorem? Can we adopt, in principle the no-cloning phenomenon as a criterion to define a micro flux of time? Can we justify this in the light of the Copenhagen interpretation of quantum mechanics? Copenhagen assumes that whenever any property of a microscopic object affects a macroscopic object, that property is “observed” and becomes a physical reality. The most famous statement in this regard is often attributed to Bohr, the founder of Copenhagen: There is no quantum world. There is only an abstract quantum description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.

This applies to cloning, it is a mental construct and is impossible to be realized. If we assume, for the sake of discussion, that cloning has taken place, then the original state will be no more available (according to the no-cloning theorem). It is as if an identity transformation has taken place, beginning with some state and ending with the same state, and as if no identified event has taken place. Hence, the no-cloning theorem is of no use in our attempt to define micro time.

Time and energy, like position and momentum cannot be simultaneously measured to arbitrary precision. This is another version of Heisenberg’s uncertainty principle. Hence the shorter the interval of time considered, the more uncertainty there will be in the energy. This allows the law of energy conservation to be suspended over very short time intervals, in fact over the shortest possible time interval. This shortest possible time interval can be considered as a quantum of time interval. If there exists a shorter interval than this assumed quantum of time interval, then the law of energy conservation would still hold during the quantum of time interval, contrary to the fact that the law of energy conservation is suspended during that interval.

The bosons which mediate the weak interactions are descendants of energy borrowed from nowhere. Owing to this, the mediation takes place during the quantum of time interval. That time has a quantum and comes in discrete packets, just like energy, can be justified based on the fact that time and energy appear as associates in all branches of physics, e.g. if, in the four-dimensional space-time, the space coordinates are transformed into momentum coordinates, then the time coordinate is transformed into energy coordinate. Also, as we have already mentioned, time and energy appear as associates in the Heisneberg’s uncertainty principle in the sense that each one of them constrains the other. Since we are causely separated from the interior of a black hole, we cannot know what is happening there. Are we similarly causely separated from the micro world? The answer is no. That is because the macro world is made of the stuff of the micro world. According to Copenhagen, our measurements of the micro world create the macro phenomena. Time is the most important of the macro phenomena. Physical time has various characters according to the variety of theories in which it appears, for instance, time in classical mechanics, time in relativity theory, time in thermodynamics, time in cosmology, time in quantum mechanics and so on. Though they are useful instruments for our practical acts, they are nothing but theoretical constructs. We cannot escape the fact that they are directly based on interactions with the micro world and indirectly on interactions within the micro world. If we accept advanced and retarded solutions of equations in macro physics, then upon probing the micro world, we must feel free to ask the following question: what time is not. We know from quantum physics that the micro world lacks identities, e.g. all electrons in the universe are copies of one and the same electron. When the particles of the micro world gather to form objects of the macro world, the objects are created with distinct identities. It appears that there is a paradox which needs reconciliation. What happens in fact is that an intended probing of the micro world transforms a quantum of time interval into a macro infinitesimal tick which contributes to the flow of the macro arrow of time. It will be inserted in that flow resulting in an updating of the flow.

Any probing of the micro world is a local event. Because of this, we can apply here the special theory of relativity. The emergence of the infinitesimal tick affects an infinitesimal transformation in Lorentzian space-time described by a pair of three vectors δω and δϕ . The pure spatial rotations are described by δω and the imaginary rotations between the time and space coordinates are described by.δϕ .

As is well known, the invariant magnitude of the infinitesimal four vector at the point, in space and time, of probing the micro world is given by:

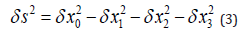
Since this is an invariant quantity, any change in the time infinitesimal 0 δ x will induce a corresponding change in the pure spatial infinitesimals. In other words, probing the micro world would give a boost to the macro space.

The emergence of identities in the macro world is related to this phenomenon. The boost creates a local agitation of particles. We conceive the agitation as a tiny constituent of a macro object .This can be explained on the basis of the fact that a human being is endowed with very dull sense of time. It may be reasonable to consider for a moment the adequate unit of length as 1 meter and the adequate unit of time as 1 second. In our sense,1 meter and 1 second are sensed roughly in the same magnitude. However, in reality, 1 second is 300 million meters. Therefore, we may think that the accuracy of our sense of time is 300 million times lower than the accuracy of our sense of length. Accordingly, we perceive the local agitation of particles as identities in space. But, as the arrow of time advances, we gradually lose their track in “time”. What if our universe homes alien whose accuracy of sense of time is greater than their accuracy of sense of length, how will they perceive identities in “time”? Can we ever communicate with them? This is what time is not. Is there any reason to regard this as unlikely or impossible?

Let us use our imagination to penetrate the micro world. According to relativity, each speck of matter has its’ own time. Interactions are always taking place in the micro world. Each interaction can be considered as an event in the micro world. Of course, such an event cannot be perceived by us in the macro world, unless we arrange for an appropriate experiment. Before doing the experiment, we can associate a complex amplitude, and hence a corresponding probability, with each possible outcome of it. In quantum theory the various possibilities combine in a superposition. Different superposed possibilities both do and do not evolve independently of each other: if one considers the probability amplitude, then the various superposed parts do evolve independently of each other; but, owing to the need to square the modulus of the amplitude, the probabilities themselves do not enjoy this property. This peculiar behavior lies at the root of difficulties that scientists have in coming to the belief that they “really understand” quantum theory. As for the macro world, the only event we can practically deal with is the certain event which has probability one. The event in the macro world as far as a theory of probability is concerned, occurs at the moment the observer takes cognizance of what has happened. The strange thing about quantum mechanics, which is, essentially, theoretical physics as at present understood, is that it does not contain the concept of an event. Since it deals with probabilities, the only event in this theory occurs now an observer looks at what has happened. If we consider the disintegration of the atomic nucleus, the theory predicts only the probability that we will have seen the Geiger counter register on or before a certain moment, but when we do see it, the probability changes abruptly to one. The abrupt change is not part of the dynamical description of the nuclear process but is due to the intrinsic nature of the pertinence of our consciousness with the world around us.

We return now to the events in the micro world. We delve in the micro world pretending that we are part of it. How will we experience the events in the micro world being part of that world? This is a sort of a thoughtful experiment. The essential character of events in the micro world is suddenness, often there will be an element of surprise for us living in the micro world. Our theory contains statements about probabilities, it does not contain accomplished facts. We can only put them in by an artifice-a very natural one but an artifice all the same. Since we have decided (with probability one) to probe the micro world, our consciousness would resonate in harmony with the quantum rules allowing our memory to be sort of a memory to register the events of the micro world, each with its’ characteristics. Everyone is harmonious with her/his memory. If our memory is to accompany us to the micro world, that is because quantum physics has elevated consciousness to the fore.

We cannot adopt any event of the micro world for fixing the moment of our arrival at that world. The micro world is an open unlimited ocean of events. We must dive into that ocean in order to track its’ events. If we must keep quantum computing absolutely isolated, we must replace the artificial decohering macro time ticks with what we can call micro time based on the events of the micro world. Although we will be encompassed by darkness and still in the micro world, yet according to quantum theory, entities will be born recurringly from nothing, shine and fade away.

This is based on another version of Heisenberg’s uncertainty principle which relates the number of light quanta with the phase of the field amplitude. Thus, if the number of light quanta has a given value zero, then the field will show certain fluctuations about its’ average value, which is equal to zero. When we view such an entity through the darkness and still, not only have the retarded waves from the entity been rushing for some period of time(from the past phase of our memory to its’ present phase)to reach our senses, but the advanced waves generated by absorption processes within our senses have reached the same period of time into the past(the past phase of our memory)completing the transaction that permitted us to feel the shining and fading of the entity. This is a type of an event in the micro world. As many entities converge another event of another type takes place. What happens if many similar “other” entities converge? Surely a similar event takes place. Not exactly, that is because identities are not conspicuous in the micro world. What we perceive is just a recurrence of the same event, or rather the same event itself. There is no “other” In the micro world. We may observe different types of events in the micro world, e.g. decay of an entity, or coalescing of many entities to produce a new one.it may happen that a decay is followed by coalescing or vice versa. In this case the two events take place as a recurring pair. As we observe a recurring pair, we may also observe a recurring multiple of associated events. We will not digress on the possible different types of events we may encounter in the micro world. There may be an infinite number of them. Let us imagine an event in the micro world of a type we did not observe. Moreover, let us associate with the imagined event some characteristics that are different from what we have registered.

Here we can make use of a theorem in probability theory due to Paul Erdos. Stated in the simplest way the theorem says:(If, in each set of events, the probability that an event does not have a certain characteristic is less than one, then there must exist an event with this characteristic). This is an existence result. It may be (and often is) very difficult to find this event, but we know that it exists. We cannot tell beforehand whether one of the events we may observe in the micro world has one of the imagined characteristics. Surely not all the characteristics of the events we observe are liable to our detection. Therefore, we can apply the above theorem and deduce that there may be an infinite number of different types of events in the micro world.

We refer to the events which we can observe and deal with in the micro world as real events, while we call the presumed events imaginary events. The main features of the macro world are radically changed upon permeating the micro world. Periodicity is replaced by recurrence and predictability is replaced by suddenness. Accordingly, we will be obsessed by a “sameness” feeling in the micro world. Although we may encounter many different types of events in the micro world, the feeling of “sameness” will infiltrate us. Here we use the term “sameness” because we have already dived in the micro world. The same phenomenon, as observed and thought of in the macro world, is called “entanglement”. All the suppositions put forth lead to the conclusion that all types of events in the micro world can be treated on the same footing, e.g. any event of whatever type in the micro world can be employed as an operator or as a micro time tick to activate a certain operator in a quantum algorithm.

The quantum vacuum is the main background of the micro world. It is a seething froth of real particle-virtual particle pairs going in and out of existence. Each pair consists of a particle and its’ antiparticle, one of which has a negative energy and is thus called “virtual”. Out of a singularity in space, which by definition really is nothing, each pair simply comes into existence. Why? Because the probability exists, because the universe is open to many (perhaps infinite) possibilities that had not previously been predicted, but nonetheless could occur at any time. This pertains to the fact that the border between the real world and the virtual world does not exist. In a sense, the real world is indistinguishable from the virtual world.

A Probabilistic Argument

Probability is the unique quantum invariant. Assume that the total number of different types of events in the micro world is n. Each event of any type recurs a number of times. We consider a sample event of each type. Let us sort the set of different types of events in ascending order according to the number of recurrences of their sample events. Next, we enumerate the resulting set of types so that the type with the minimum number of recurrences of its’ sample event is numbered one, while the type with the maximum number of recurrences of its’ sample event is numbered n. There will be no loss of generality in the following mathematical treatment if we assume that the number of recurrences of any sam ple event of whatever type coincides with the new number given to its’ type after carrying out the enumeration procedure. This means that we would observe the event of type one only once, while we register n recurrences of the event of type n. The statistics of the recurrences in this case are:

Since all types of events in the micro world can be treated on the same footing, the probability of observing an event of some type coincides with the probability of identifying its’ type which is 1/n.

We make here an interlude to review the method of calculating the mean and variance by using generating functions. Let us suppose that we have a generating function whose coefficients represent probabilities:

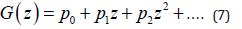
Here p_k is the probability that some event has a value k. We wish to calculate the quantities:

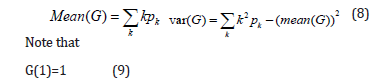
Since G(1) = p₀ + p₁ +.... is the sum of all possible probabilities. Similarly, since

we have mean (G)=

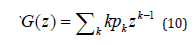
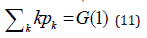
It is a simple exercise to prove that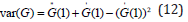

We return now to our problem. The generating function in this situation is

We find after some calculations that

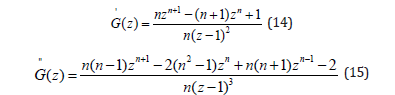
Now to calculate the mean and variance, we need to knowG(1) and G(1) ;but the form in which we have expressed these equations reduces to 0/0 when we substitute z=1. This makes it necessary to find the limit as z approaches unity. This can be done using L’ Hospital’s rule. We find after some calculations that

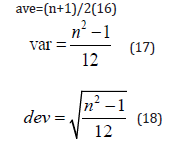
Note that the ave, var and dev increase with the increase of n. This means that a limited number of events should be used as micro time ticks and as operators in a quantum algorithm.

Assume that the total number n of types of events in the micro world includes imaginary types of events. This is justified since an imaginary event may materialize suddenly and be observed. Suppose there is a probability p that a real event shows at each observation; what is the average number of real events which will be observed? What is the standard deviation? Let p_nk be the probability that k real events will be observed and let G_n(z) be the corresponding generating function. We have clearly

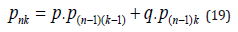
Here, q=1-p is the probability that an imaginary event materializes and shows at each observation. We argue from equation (19) that

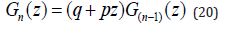
Using the obvious initial condition

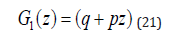
we get

Hence, we have for the statistics of the number of considered types of events:

When the standard deviation is proportional to 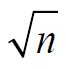and the difference between maximum and minimum is proportional to n, we may consider the situation” stable” about the average.

We deduce that, to improve on the situation, we have to take the imaginary types of events into consideration. But can we really make use of the imaginary types of events? The answer is in the affirmative. We refer here to the well-known quantum rule:

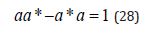
Where a is the annihilation operator, and a* is the creation operator. The rule says that if in a first process the creation operator is applied followed by the annihilation operator, and in a second process the annihilation operator is applied followed by the creation operator; then the outcome of the first process exceeds that of the second process by exactly one entity. This assures us that we can always bring an imaginary event to the circle of action.

If we categorify the operators a and a*we get the stuff operators A and A* . A categorified version of the rule (28) can be proved by using a structure type F. The isomorphism proved in this case is:

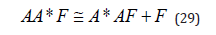
And the categorified version of (28) would be

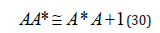
Here ≅ refers to an isomorphism. The interesting thing about such a proof is that it reduces a fact about quantum theory to a fact about finite sets.

In other words, rule (28) can be regarded as an abstract mathematical equality, rather than interpreted as a physical formula. It can be obtained by decategorifying the isomorphism (30). In essence, it is a rule of the mind. Similarly, following the same trend of thought, we can employ both the real and imaginary types of events as micro time ticks and as operators in quantum algorithms.

Conclusion

In a previous paper of mine entitled “Thermodynamic and Quantum Mechanical Limitations of Electronic Computation”, I derived a number of relations pertaining to these limitations. Thermodynamic limitations are essentially macroscopic in nature, they can be dealt with in the macro world. Although quantum mechanical limitations have their basis in the micro world, yet I was able to express their final effects in qualitative terms which find their suitable place in the macro world. Not to mention all these effects, the most important of them manifests itself in the result which says that assignments occurring at later times are prone to higher uncertainties. Also, that no closed computer system, however constructed, can run programs of infinite lengths (practically very long programs). The limitations mentioned in my previous paper can be termed physical, since they can be dealt with in the macro world. The issue presented in this paper is totally different. The whole quantum computer must be isolated without any interaction, whatsoever, with the rest of the world. Whenever the limitations of quantum computing actualize, their action must in turn be isolated from the rest of the world. Also, their handling, if possible, must take place in isolation. Accordingly, the limitations of quantum computing are termed natural. Every detail in quantum computing belongs to the micro world. All the real and imaginary events must be probed and scrutinized in order to employ them in the quantum algorithms. All the theoretical components of a quantum algorithm must be put in a one to one correspondence or mapping with suitable real and/or imaginary events. A sort of an assignment is ensued from such a mapping, where each operator or time tick or any other component in the theoretical quantum algorithm is replaced by a real or imaginary sample event from the micro world. We call this assignment a quantum assignment. It differs from the classical assignment, where each component of the program is projected onto a sector of the memory of the digital computer. The classical assignment is effectuated deterministically, while the quantum assignment is anticipated probabilistically.

Assume that the cardinality of the set of probable real and imaginary sample events in the micro world is m. Moreover, suppose that a quantum algorithm encompasses j theoretical components. To make use of the set of probable real and imaginary sample events, the following condition must be satisfied:

It is well known that the number of subsets of the original set of real and imaginary probable sample events, each with cardinality j, is

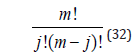
Consider one of these subsets. The probability that a given component of the theoretical quantum algorithm can be replaced by an element of the subset is

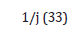
Hence the probability that each component of the theoretical quantum algorithm can be replaced by an element of the subset is

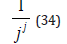
Therefore, the probability that all components of the theoretical quantum algorithm can be replaced by events of the original set of real and imaginary probable sample events is

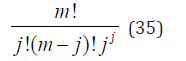
It is a rather small probability. Yet, because the number of probable real and imaginary events of the micro world is immense, one would be content with the probability that all the components of a quantum algorithm can be replaced by real and imaginary events of the micro world.

The replacements are to take place in the micro world as the essential structure of the theoretical quantum algorithm is immersed in that world. The immersion can be accomplished by applying suitable quantum rules for the preparation of states. Total isolation is the main and only prerequisite for the accomplishment of a quantum computing. According to quantum physics, the existence of a physical system is related to measurement. A measurement by definition, is a physical interaction, and physical interactions obey Heisenberg’s uncertainty principle. According to the energy version of the principle, if a limited time T is available for making the measurement, then the energy of the system cannot be determined better than within an amount of order  / T . This is equivalent to

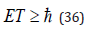
Where E is the energy of the system, T the period of measurement and  Planck’s constant divided by 2π In particular, if a system is unstable having a finite lifetime T, its’ energy cannot be measured to within an accuracy better than about  / T .

Let the measurement in our case be the replacement of a component of the theoretical quantum algorithm by a real or imaginary probable sample event (as assessed and estimated probabilistically in the macro world). Denote by F the rate of replacement measured in bits of information of the theoretical quantum algorithm per second of macro time. Then F and T (macro time of replacement) would be reciprocals. We deduce that no isolated quantum computing system can have F exceeding E /  .

Let M be the total mass of the system; which includes the mass equivalent of the energy employed in the replacement processes (as assessed and estimated probabilistically in the macro world), as well as the mass of the materials of which the computer and its’ power supply are made. In our case, the structural mass outweighs the mass equivalent of the replacement processes energy. However, the mass equivalent of the energy can be computed by applying Einstein’s formula: energy=(mass)x(square of velocity of light). In other words, the total mass equivalent of the invested energy cannot exceed M, the total mass of the system. We would have

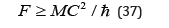
This result tells us that the rate of replacement can be increased at will by increasing the total mass of the system. Although quantum computing faces serious limitations, all of them can be coped with. We mention in this context quantum macroscopic effects which can be employed in the replacement processes. Take for example the Casimir effect which is a macroscopic quantum effect. It is expected to hold for any sort of quantum field. Consider the gap between two plane mirrors as a cavity. All electromagnetic fields have a characteristic” spectrum” of many different frequencies. In a free vacuum, all of the frequencies have the same probability and importance. But inside a cavity, where the field is reflected back and forth between the mirrors, the situation is different. Vacuum fluctuations are suppressed or enhanced depending on whether their frequency corresponds to a cavity resonance or does not. The most probable enhanced vacuum fluctuations can be employed in the replacement processes. At a cavity- resonance frequency, the radiation pressure is stronger inside the cavity than outside, and the mirrors are therefore pushed apart. Out of resonance, in contrast, the radiation pressure inside the cavity is smaller than that outside, and the mirrors are drawn toward each other. Each of these results is an event that can be used in the replacement processes.

References

1. Kalitzin NS (1975) Multitemporal theory of relativity. Publishing House of the Bulgarian Academy of Sciences, Bulgaria.
2. Fok Al AF (2016) Thermodynamic and quantum mechanical limitations of electronic computation. Journal of Information Technology & Software Engineering.
3. Wilf HS (1994) Generating functionology. Academic Press, USA
4. Aigner M, Gunter MZ (2002) Proofs from the book. Springer-Verlag, Germany.
5. Landshoff P, Metherell A (1979) Simple quantum physics. Cambridge University Press, UK.
6. Krips H (1990) The metaphysics of quantum theory. Oxford University Press, UK.
7. Mcmahon D (2008) Quantum computing explained. John Wiley& Sons Inc, USA.
8. Yanofsky NS, Mannucci MA (2008) Quantum computing for computer scientists. Cambridge University Press, England.
9. Thaller B (2005) Advanced visual quantum mechanics. Springer Science+ Business Media, Inc, Germany.
10. Greiner W (1994) Quantum mechanics an introduction. Springer-Verlag, Germany.
11. Spivak SA (2014) Category theory for the sciences. MIT Press, USA.
12. Flapan E (2016) Knots, molecules, and the universe: an introduction to topology. The American Mathematical Society, USA.