Assessment of Annual Rainfall Probabilities of Zabol Using Fuzzy Probability Rules

The probability of rainfall with different amounts in different time scales has many applications in meteorology and hydrology, and in engineering hydrology and water resources, it is used to design water structures. It also has an important role in determining and evaluating the risks caused by heavy and intense rainfall. To estimate the probability of occurrence of various events, including rainfall, both classical probability laws and fuzzy probability laws can be used. Fuzzy sets were introduced by Zadeh [1] and then the laws of fuzzy probabilities related to fuzzy events and the method of calculating their probability were first established and presented by him [2]. The concept of fuzzy sets is one of the most basic and efficient tools in intelligent computing. Fuzzy sets can provide suitable and appropriate solutions to overcome problems related to control, classification of patterns, reasoning, modeling, design of algorithms, and design and planning of the operation of various systems. Haghighat jou [3] has investigated the probability of occurrence of monthly and annual rainfall at the Zabol synoptic weather station for 50 years using the exponential distribution and has concluded that the mentioned distribution is suitable for frequency analysis of Zabol rainfall. Furthermore, exponential distribution has one-parameter and is a simple one. The main goal of this research is to investigate the effectiveness and ability of fuzzy probability laws to calculate the probability of annual rainfall in Zabol, which is located in a hyper-arid climate. It is also a comparison of the results obtained with the laws of classical probability, which are usually used for the statistical analysis of the mentioned data.

The data used in this study are the annual rainfall data of Zabol synoptic weather station during 1961 to 2010 for 50 years. These data were collected from the country’s meteorological yearbooks [4]. The statistical characteristics of the data used are listed in Table 1.

Table 1:Statistical characteristics of annual rainfall in Zabol during the years 1961 to 2010.

Calculating the probability of annual rainfall in Zabol using fuzzy probability laws

Calculating the probability of occurrence of fuzzy events in the general state. Let S be a sample space and its probability value is P. If a fuzzy event is from the desired sample space, then the probability of occurrence of the fuzzy event, if the desired sample space is discrete, is defined as follows [2,5].

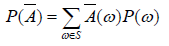
In the latter relation, is the degree of membership of a fuzzy event. The latter relation is a generalization for defining the probability of occurrence of a conventional event. To calculate the probability of annual rainfall in Zabol using fuzzy probability rules, the sample space is the annual rainfall data, which are divided into seven categories according to Table 2. In general, each subset of the desired sample space constitutes a fuzzy event. To specify the events, we express them with linguistic variables or verbal expressions. These linguistic variables include seven variables (each variable belongs to one category of the frequency distribution Table 2 mentioned in the section) very low, low, relatively low, average, relatively high, high, very high. For each linguistic variable, we have a degree of membership according to Table 3 below [6]. It should be noted that the degree of membership belonging to the linguistic variables or verbal expressions in Table 3 is for analyzing the probability of high rainfall, and if we want to analyze low rainfall, we must adjust the membership degrees of the linguistic variables or verbal expressions according to Table 4.

Table 2:Frequency distribution of annual rainfall in Zabol during the years 1961 to 2010.

Table 3:Degree of membership of fuzzy sets corresponding to different linguistic variables or verbal expressions to calculate the probability of high rains.

Table 4:Degree of membership of fuzzy sets corresponding to different linguistic variables or verbal expressions to calculate the probability of low rains.

Considering Table 2 and taking into account that the relative frequency of each category (based on the classical probability law) indicates the probability of rainfall related to the desired category or class is obtained as in Table 5. Of course, the above-mentioned article is correct if the sum of frequencies theoretically tends to infinity. Here, as listed in Table 2, the sum of the frequencies is equal to 50, which seems sufficient and the aforementioned condition is met. Also, to calculate the fuzzy probability of low or high rainfall in Zabol, the status of each category is specified in the third column. In the fourth and fifth columns of the Table 4, degrees of membership are written to calculate the probability of occurrence based on fuzzy probability. According to formula 1, the probability of low rainfall in Zabol based on the fuzzy probability law is equal to 0.61 (the sum of the product of the numbers in columns 2 and 4 of Table 5 and the probability of heavy rainfall is 0.13 (the sum of the product of the numbers in columns 2 and 5 of Table 5 is calculated. If we compare the results of these calculations with the probability of rainfall based on the classical probability listed in Table 5, the result is that the probability of rainfall is very low, low and relatively low (78+30+24, all in percent) [7-9]. Likewise, the probability of heavy rainfall is 12% (10+0+2). According to the available evidence, it seems that the results of fuzzy probability are more accurate than the results of classical probability.

Table 5:Membership degree values for calculating the probability of low and high rainfall based on fuzzy probability.

This article has been prepared with the financial support of University of Zabol, Vice-Chancellor of Research and Technology and research contract number IR-UOZ-GR-0303, by which the authors express their gratitude to University of Zabol.

1. Zadeh LA (1965) Fuzzy sets. Information and Control 8(3): 338-353.
2. Zadeh LA (1968) Probability measures of fuzzy events. Journal of Mathematical Analysis and Applications 23(2): 421-427.
3. Haghighat JP (2017) Analysis of monthly rainfall frequency in Zabol using exponential distribution. Iran.
4. Meteorological yearbooks of the entire country, from 1961 to 2010. Tehran.
5. Taheri SM, Mashinchi M (2008) An introduction to probability and fuzzy statistics. Kerman.
6. Pedrycz W, Gomide F (1998) An introduction to fuzzy sets, analysis and design. Computer Science.
7. Taheri SM (2001) Calculating the probability of an event based on fuzzy observations, report of the third seminar on probability and random processes. pp. 163-176.
8. Bazargan LA (2005) Applied Statistics.
9. Yager RR (1979) A note on probabilities of fuzzy events. Information Sciences 18(2): 113-129.